加连梁柱串联隔震系统的弹性屈曲

杜永峰 ，朱前坤，李慧

(1. 兰州理工大学 防震减灾研究所，甘肃 兰州，730050；2. 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，甘肃 兰州，730050)

当隔震建筑上部结构有承重墙体，或大柱网的框架结构、各柱底轴力和剪力相差较大，或地下室层高较高时，隔震建筑可采用加连梁柱串联隔震系统方案[1]。叠层橡胶支座由薄橡胶片与钢板分层叠合而成，具有很大的竖向刚度、较小的水平刚度和很大的变形能力。水平刚度小能够延长隔震结构自振周期从而达到减少上部结构地震作用的效果，但同时会伴有较大的隔震层水平位移，从而显著降低临界荷载值。这一特性引起了学者的极大关注。Gent[2]基于Harings理论研究了叠层橡胶支座的稳定性。Koh等[3]为了简化计算提出了双自由度力学模型，分析了叠层橡胶支座在大水平位移时的稳定性。Nagarajaiah等[4]改进Koh-Kelly双自由度力学模型得到了更精确的临界荷载和水平刚度，Buckle等[5]用试验验证了改进模型的有效性。随着高层隔震建筑的大量出现，Kelly等[6-7]分析了叠层橡胶支座的竖向刚度和拉伸屈曲。Liu等[8-9]提出橡胶支座的一些基本概念，较系统地建立了橡胶支座各种力学性能的计算理论和评价方法。周锡元等[10-11]在Harings和Gent研究基础上建立了柱串联隔震系统的分析模型，推导出柱串联隔震系统的水平刚度计算公式及临界荷载控制方程。关于工程中普遍使用的加连梁柱串联隔震系统研究还没有相关报道。本文作者在前人研究的基础上，基于传递矩阵法[12]，推导出隔震系统端部状态变量与任意截面的内力和位移值之间的关系，可以较容易地得到临界荷载控制方程，避免了繁琐的力学推导过程，并进一步考虑连梁参数变化系统临界荷载的影响。

1 稳定性分析的传递矩阵

加连梁柱串联隔震系统由叠层橡胶支座、地下室悬臂柱和连梁组成如图1所示。加连梁柱串联隔震系统可能有两种失稳性态，对称失稳和反对称失稳。反对称失稳的临界荷载比对称失稳小得多，因此，在实际工程计算中只考虑反对称的情况[13]。反对称失稳模型如图2所示。

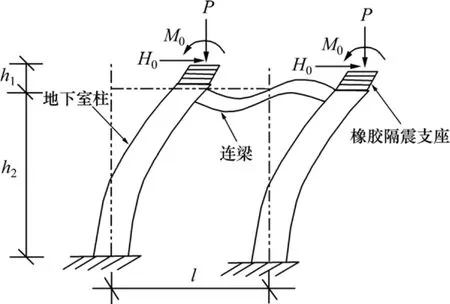
图1 串联隔震体系模型Fig.1 Series isolation system model

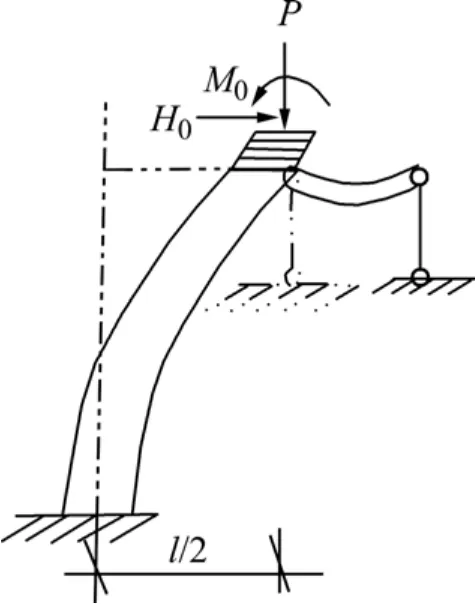
图2 反对称失稳模型Fig.2 Antisymmetric instability model

1.1 稳定性分析的场矩阵

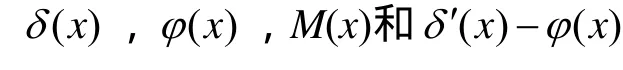
式中：kb和ks分别为橡胶支座等效弯曲刚度和剪切刚度[15]，

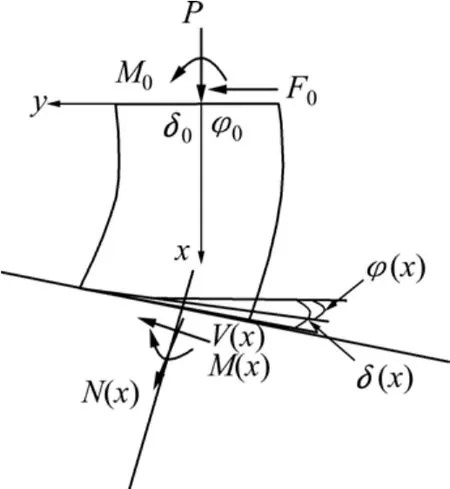
图3 橡胶支座隔离体Fig.3 Isolation rubber bearing body

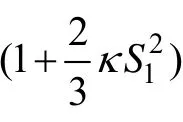
由文献[6, 10-11]可得隔离体的任意截面的内力和位移：

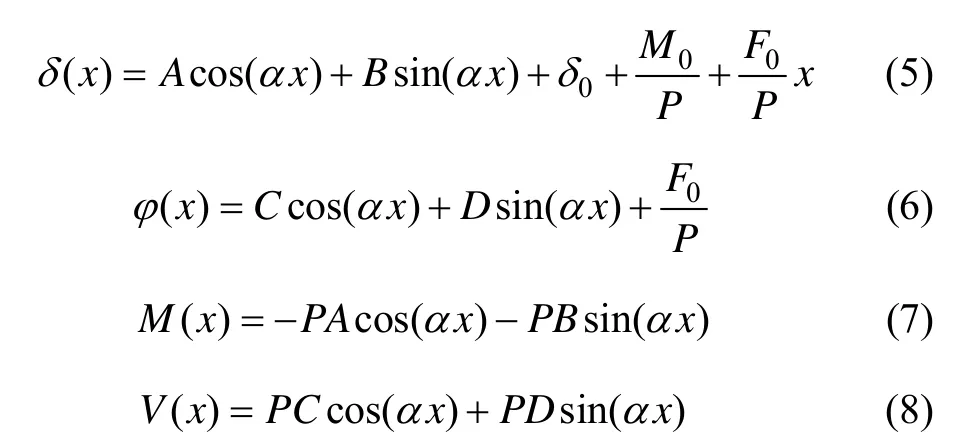
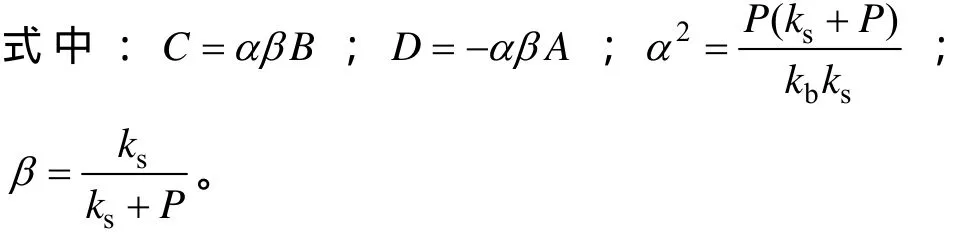
令x=0，由式(5)和式(8)可得：

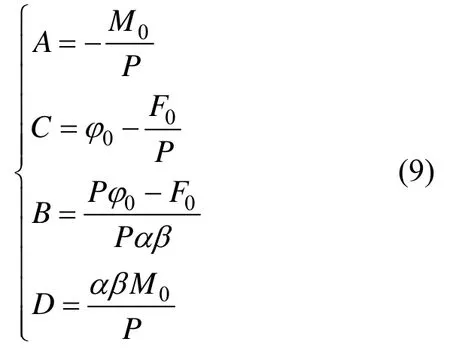
把式(9)代入式(5)和(8)可得：

把式(10)～(13)写成以下矩阵形式：

式中：

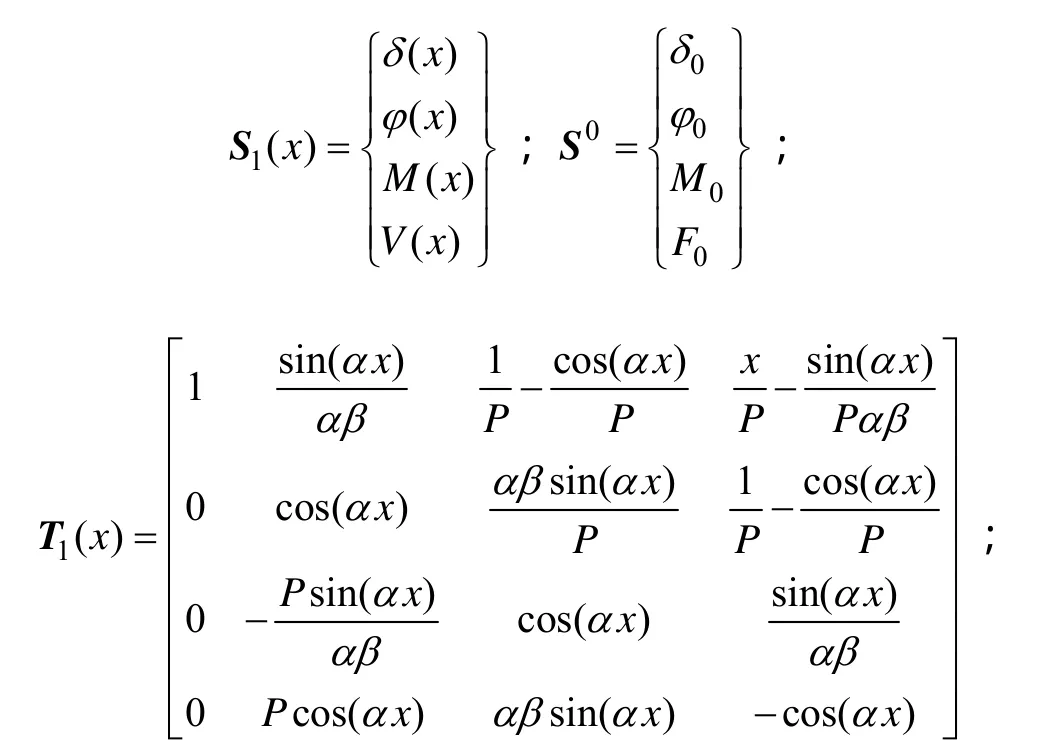
S0为初始状态变量；S1(x)为x截面状态变量；T1(x)为传递矩阵。由式(14)可知：若初始状态变量已知，则可以容易求出橡胶隔震支座任意截面处的变形和内力。S1(h1)为支座末端的状态变量；T1(h1)为稳定性分析的场矩阵。

1.2 稳定性分析的点矩阵

连梁等效成一抗弯弹簧如图4所示，弹簧刚度系数为 K =3 （EI ）3/（ l /2） ，（EI）3为连梁的抗弯刚度，则由连接处的平衡关系和连续条件可得：

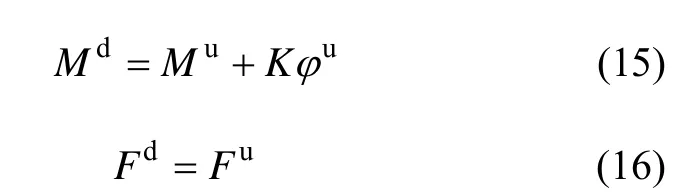
式中：上标d和u表示连接处上段和下段。

写成矩阵形式为：

式中：

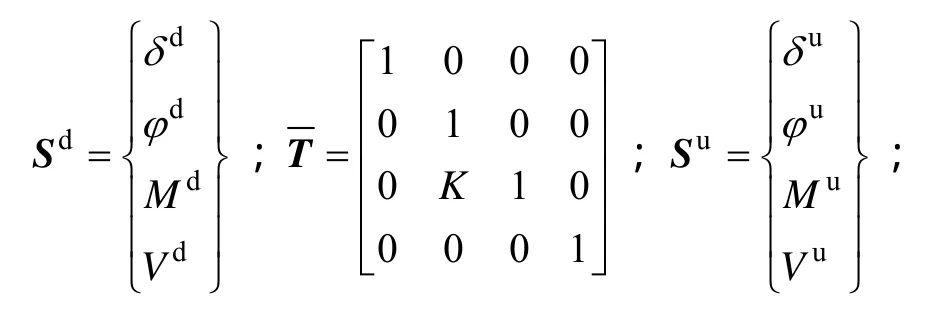
图4 等效抗弯弹簧Fig.4 Equivalent spring

2 临界荷载控制方程

地下室柱上端状态变量 S20与下端的状态变量 S2的传递关系为：

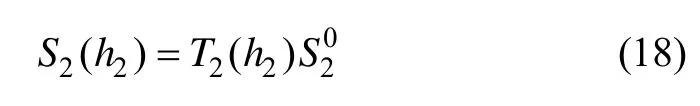
橡胶隔震支座与地下室柱交界面应满足：

将式(19)代入到式(18)可得：

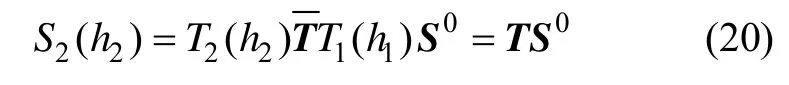
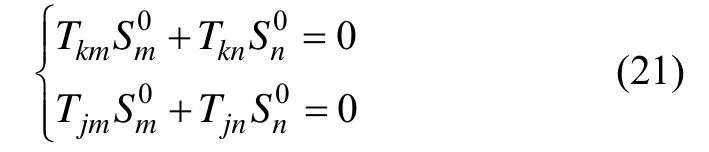
式(22)即为加连梁柱串联隔震系统稳定分析的普遍方程，其特征值即为其临界荷载。在实际工程中，橡胶支座上端纵横向连接梁刚度比橡胶支座刚度大得多，可认为支座上端的转角为零即φ0=0，地下室柱固定在基础上即 δ( h1+ h2) =0和 φ( h1+ h2) = 0。假设F0= 0，由式(18)可得加连梁柱串联隔震系统临界荷载的控制方程：

当K=0，可得无连梁柱串联隔震系统临界荷载的控制方程：

地下室柱刚度无穷大即隔震支座直接固定在基础上即 δ( h1) =0和φ( h1)= 0，可得单个支座的临界荷载的控制方程：

式(25)与文献[6]中临界荷载的控制方程相同。

3 算例分析

考查实际工程中由混凝土强度等级为C30、截面面积(长×宽)为600 mm×600 mm、高为2 500 mm的地下室柱；连梁采用混凝土为C20、跨度为5 000 mm、截面面积(长×宽)为500 mm×200 mm；橡胶隔震支座GZP 500和GZP 600组成的加连梁串联隔震系统。隔震支座参数如表1所示。GZP 500和GZP 600组成的隔震系统设计所承受荷载分别为2.945 2 MN和4.241 2 MN，利用式(23)求得加连梁串联隔震系统临界荷载分别为11.062 MN和22.813 2 MN，满足稳定性要求。

图5所示为其他参数保持不变，连梁参数变化对临界荷载的影响，并与无连梁和单个支座的临界荷载的对比。从图5(a)可以看出：连梁弹性模量从22 GPa增加至 36 GPa, 加连梁柱串联隔震系统临界荷载从10.125 6 MN增加到10.249 1 MN，增加1.22%；从图5(b)可以看出：连梁惯性矩从0增加到10.8×10-3m4，加连梁柱串联隔震系统临界荷载线性增加从 9.803 1 MN到10.592 3 MN，增加8.05%；从图5(c)可以看出：随着连梁与地下室柱的线刚度比从0增加到1.0，加连梁柱串联隔震系统临界荷载从 9.803 1 MN增加到10.592 3 MN，增加8.05%。可见：增加连梁对提高柱串联隔震系统的临界荷载有作用，但不显著。无连梁柱串联隔震系统和单个支座的临界荷载分别是 9.801 MN和10.906 MN，可见：引入了地下室柱，临界荷载降低 10.1%。所以，隔震建筑采用地下室柱方案在增加了地下室功能基础上，稳定性相对与单个支座降低程度有限。一般而言，工程中橡胶隔震支座的水平刚度仅为钢筋混凝土柱1/10左右，所以，钢筋混凝土柱水平位移相对与橡胶支座可忽略不计，钢筋混凝土柱对橡胶支座只起到转动弹簧的作用，而转动弹簧刚度系数对橡胶支座作用可近似认为足够大，故引入地下室柱对于降低稳定性的有影响，但不明显；而增加连梁对增大转动弹簧刚度系数影响有限，故对提高柱串联隔震系统临界荷载作用不大。

表1 叠层橡胶支座参数Table 1 Laminated rubber bearings parameters

图5 临界荷载与连梁参数变化曲线Fig.5 Relationship between critical buckling loads with parameter variation of coupling beam

4 结论

(1) 增加连梁对提高柱串联隔震的系统的临界荷载有作用，但效果不明显。

(2) 无连梁柱串联隔震系方案增加了地下室功能，虽然降低了临街荷载，但从经济性、安全性和使用功能综合考虑，隔震建筑下部结构应优先选用地下室独立柱方案。

[1] 党育, 杜永峰, 李慧. 基础隔震设计及施工指南[M]. 北京:中国水利水电出版社, 2007: 84-85.DANG Yu, DU Yong-feng, LI Hui. Direction of design and construction on base-iaolation[M]. Beijing: China WaterPower Press, 2007: 84-85.

[2] Gent A N. Elastic stability of rubber compression springs[J].Journal of Engineering Mechanics, 1964, 6(4): 318-326.

[3] Koh C G, Kelly J M. A simple mechanical model for electrometric bearings used in base isolation[J]. Journal of Engineering Mechanics, 1988, 30(12): 933-943.

[4] Nagarajaiah S, Ferrell K. Stability of electrometric seismic isolation bearings[J]. Journal of Structural Engineering, 1999,125(9): 946-954.

[5] Buckle I, Nagarajaiah S, Ferrell K. Stability of electrometric isolation bearings: Experimental study[J]. Journal of Structural Engineering, 2002, 128(1): 3-11.

[6] Kelly J M. Tension buckling in multilayer elastomeric bearings[J]. Journal of Engineering Mechanics, 2003, 129(12):1363-1368.

[7] Warm G P, Whittaker A, Constantinou M. Vertical stiffness of electrometric and lead-rubber seismic isolation bearings[J].Journal of Structural Engineering, 2007, 133(9): 1227-1236.

[8] Liu W G, He W F, Feng D M, et al. Vertical stiffness and deformation analysis models of rubber isolators in compression and compression-shear states[J]. Journal of Engineering Mechanics, 2009, 135(9): 945-952.

[9] Yang Q R, Liu W G, He W F, et al. Tensile stiffness and deformation model of rubber isolators in tension and tension-shear states[J]. Journal of Engineering Mechanics, 2010,136(4): 429-437.

[10] 周锡元, 韩淼, 曾德民, 等. 橡胶支座与R/C柱串联隔震系统水平刚度系数[J]. 振动工程学报, 1999, 12(2): 157-165.ZHOU Xi-yuan, HAN Miao, ZENG De-min, et al. Horizontal rigidity coefficient of the serial system of rubber bearing with column[J]. Journal of Vibration Engineering, 1999, 12(2):157-165.

[11] 周锡元, 韩淼, 曾德民, 等. 组合橡胶支座及橡胶支座与住串联系统的水平刚度计算方法[J]. 地震工程与工程振动, 1999,19(4): 67-75.ZHOU Xi-yuan, HAN Miao, ZENG De-min, et al. Calculation method of lateral stiffness of combined rubber bearing and serial system of bearing with columns[J]. Earthquake Engineering and Engineering Vibration, 1999, 19(4): 67-75.

[12] 刘庆潭. 材料力学教程[M]. 北京: 机械工业出版社, 2006:313-321.LIU Qing-tan. Course of material mechanics[M]. Beijing: China Machine Press, 2006: 313-321.

[13] 王仕统. 结构稳定[M]. 广州: 华南理工大学出版社, 1997:102-108.WANG Shi-tong. Structural stability[M]. Guangzhou: South China University of Technology Press, 1997: 102-108.

[14] 胡海昌. 弹性力学的变分原理及其应用[M]. 北京: 科学出版社, 1982: 139-144.HU Hai-chang. The variational principles in theory of elasticity and its application[M]. Beijing: Science Press, 1982: 139-144.

[15] 周福霖. 工程结构减震控制[M]. 北京: 地震出版社, 1997:85-86.ZHOU Fu-lin. Structure vibration control[M]. Beijing:Earthquake Publishing House, 1997: 85-86.