自适应混沌粒子群优化的粮食应急点选址研究

肖 乐，吴相林,张雪萍

（1.华中科技大学 控制系，湖北 武汉 430074; 2.河南工业大学 信息科学与工程学院，河南 郑州 450001）

自适应混沌粒子群优化的粮食应急点选址研究

肖 乐1,2，吴相林1,张雪萍2

（1.华中科技大学 控制系，湖北 武汉 430074; 2.河南工业大学 信息科学与工程学院，河南 郑州 450001）

针对粮食应急点选址，将“运输时间最小”和“应急开始最早”作为目标，建立了相应的优化模型.利用基于粒子群的K-Medoids聚类算法进行求解，为了避免过早地陷入局部最优，提出了自适应混沌粒子群优化算法.该算法利用粒子与已知全局最优粒子的欧式距离来判断粒子群当前状态，并将其作为确定混沌扰动范围的启发信息，可以有效地提高最优解的精度.试验表明该算法优于传统的演化算法，较好地解决了粮食应急点选址问题.

粮食应急点；选址；聚类；自适应混沌粒子群算法；距离启发信息

0 引言

突发事件下的粮食供给保障直接关系到人民生活安全和社会稳定.近年来，国家和各省市均出台了“粮食应急预案”，对紧急情况下的粮食供给和流通提出了较高的要求.应急粮食与与其他应急物资相比有其特殊性，由于数量和体积较大，本身也易发生霉变、虫灾和鼠害，必须建立临时的粮食应急点进行储藏和保管.粮食应急点主要从其他国有储备粮库接收并储存足够的粮食，为其周围地区进行救援.粮食应急点的选址和建设一般是在省级区域进行，不同于在一个城市中的多应急服务设施点的选址问题[1].粮食应急点选址问题的研究对促进事发区域稳定，提高政府应急响应能力等有着十分重要的意义.

粒子群优化(PSO)算法是由Kennedy等[2-3]提出的一种进化算法，它源于对鸟类捕食过程中迁徙、聚集行为的模拟.因为PSO算法参数简单、容易实现、可并行处理、鲁棒性好、能以较大的概率收敛到全局最优解，所以粒子群优化算法得到了广泛关注.与所有的演化算法类似，由于加入了正反馈，粒子群优化算法也存在早熟收敛现象，在较复杂的高维、多峰搜索问题中表现得尤为明显.笔者在处理粮食应急点选址这一实际问题中，通过对基本粒子群算法改进，提出了一种自适应混沌粒子群算法，在解决上述问题中得到了较好地应用.

2 粮食应急点选址数学模型

假设某一地区发生自然灾害或突发事件，亟需大量的粮食供应，现根据需求在事发区域中建设d1,d2,…dk个粮食应急点，已知每个应急点的到各个救援目标的障碍约束下运输时间和每个粮食应急点的最早应急时间.要求在一定的区域X和在一定时间T内，满足该区域人口应急需求的前提下，求得最佳的d1,d2,…dk位置，使得应急方案的总运输时间最小和最大应急开始时间最早.

基于上述分析，粮食应急点选址问题本质是在诸多约束条件下的一个多目标优化问题.该问题建立在以下条件之上：

1）在一定区域范围内进行粮食应急点选址；

2)%考虑到区域内既有的和突发事件下新增的各种障碍物对选址的影响，粮食应急点只能选择在适宜建设的地址上；

3)%每个出救目标只接受一个应急粮库的救援；

4)%方案中的各粮食应急点的最大最早应急时间必须满足应急要求；

5)%方案中各应急点到其所服务的救援目标最长时间必须满足应急要求；

6)%在应急要求下，不考虑应急点的建设成本和运输成本.

考虑粮食应急特点，在针对上述两个目标建立优化模型时，需要引入相应影响因子.

2.1 总运输时间最小和最大应急开始时间最早

问题要求找到X的一个划分Pk={D1,D2,…,Dk}，使其目标函数值最小.建立目标模型如下：

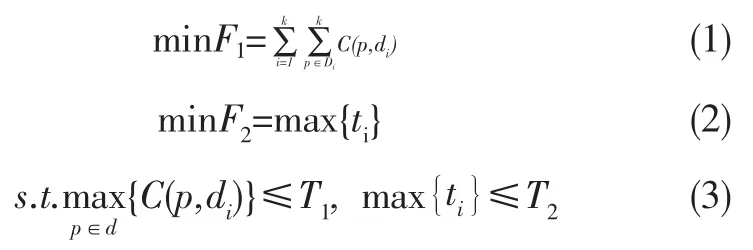
式中：di表示第i个的应急点，di∈Di，C(p,di)为在一个划分区域中应急点到救援目标障碍条件下的时间开销. ti为第i个粮食应急点所能提供的最早应急时间.T1为应急活动允许应急点到其救援目标的最长时间，T2为整体应急响应开始的最晚时间.

2.2 待救援目标紧急响应程度

在公共突发事件或自然灾害中，待救援目标所需救援的紧急程度和受影响人口的数量不尽相同.在粮食应急选址时需要考虑每个救援目标的响应紧急程度，从而使粮食应急点选址兼顾及时性与公平性.这里引入一个紧急因子λj(j=1,2,…,n)表示救援目标pj的应急紧急程度，λj越大表示救援目标pj越重要，该值可由专家给出.则式（1）变为：

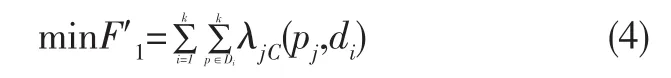
用式（5）来求得上述问题的多目标最优解.

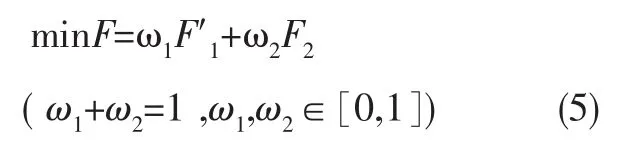
式中：ω1、ω2是控制因子，不同的值代表对不同目标的关注程度，应用时视粮食应急实际情况而定.

式（4）可以看作聚类问题，解决此类问题较典型的方法有K-Mediods算法、K-Means算法和CLARANS算法.CLARANS算法较多用于大数据量的情况下. K-Means算法选取类中对象的平均值作为中心，有时中心可能刚好落在障碍上，在实际应急中是不允许的.而K-Mediods算法选择类中的一个对象作为中心点，这样保证类中心不会落在障碍上.利用带障碍约束的K-Mediods聚类算法提高实用性.但K-Mediods聚类算法具有对初始值的随机选取敏感，很容易陷入局部极值等缺点，粒子群算法在处理聚类问题上有一定的优势.为了解决基本粒子群算法过早收敛问题，将基本粒子群算法与混沌系统相结合，利用混沌系统的伪随机性及遍历性对粒子加以扰动，以提高全局收敛的概率和速度.

3 混沌粒子群优化算法

混沌粒子群算法是在基本粒子群算法中加入了混沌初始化和混沌扰动环节来实现的.下面首先给出基本粒子群算法介绍.

3.1 基本粒子群算法

PSO算法采用“群体进化”的概念，利用单个粒子的适应度值大小来评价该粒子的优劣.每个粒子对应问题的一个可能解，具有位置和速度.粒子位置对应的目标函数的值就是该粒子的适应度.算法先随机生成一组初始粒子，然后对每个粒子迭代，最后得到一个解.每次迭代中，粒子更新通过跟踪个体极值位置pbest(即粒子本身经历过的最优解)和全局极值gbest(即全题粒子群经历过的最优解)实现.

所有粒子根据下面公式来更新自己的速度和位置：

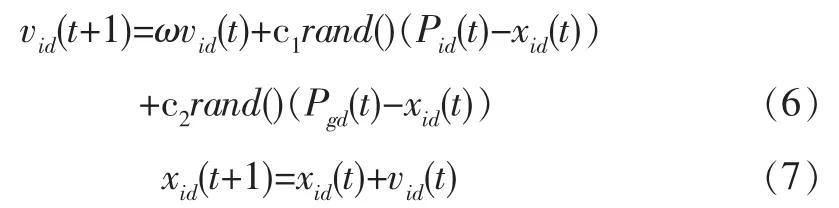
式中：vid表示第i个粒子在第d维上的速度；xid表示第i个粒子在第d维上的位置；ω，c1，c2表示群体的认知系数，ω一般介于于（0，1）之间的随机数，c1，c2取（0，2）之间的随机数.用Pi=(pi1,pi2,…,piD)，i=1,2,…,n表示第i个粒子迄今为止搜索到的最好位置，也称为个体极值pbest.用Pg=(pg1,pg2,…,pgD)表示整个粒子群迄今为止搜索到的最优位置，也称为全局极值gbest.

为防止粒子远离搜索空间，粒子的每一维速度vid的值被限定在一个最大速度vdmax(vdmax＞0)内，如果某一维更新后的速度超过用户设定的vdmax，那么这一维的速度就被限定在vdmax，即若vid＞vdmax时，vid=vdmax或vid＜－vdmax时，vid=－vdmax.

3.2 混沌粒子群优化算法

针对基本粒子群优化算法的不足，利用混沌运动的遍历性，产生大量初始群体，从中选择较优的初始群体，在迭代过程中，对当前粒子个体产生混沌扰动，以使解跳出局部极值区间.

Logistic映射是一个典型的混沌系统，迭代公式如下：

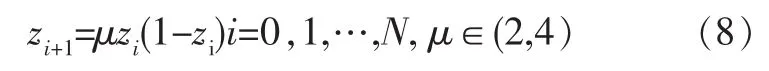
式中：μ为控制参量，当μ=4时，Logistic完全处于混沌状态.

设求解n维的优化问题：

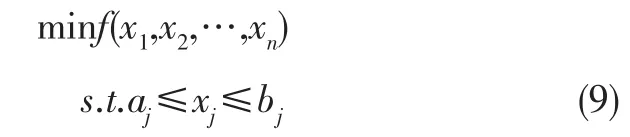
解上述优化问题的混沌粒子群算法的程序框架为：

Step1：设定粒子数m，初始化混沌系统.随机产生一个n维、每个分量取0～1之间的数值，生成向量Z1= (z11,z12,…,z1n).根据式（8），得到m个Z1,Z2,…,Zn.将Zi的各个分量加载到优化变量的取值范围：

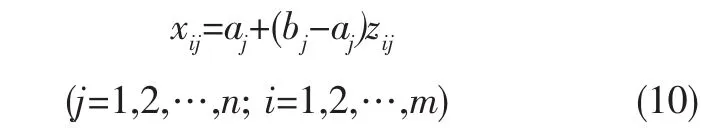
计算目标函数，初始化pbest和gbest，随机产生m个速度.

Step2：根据当前位置和速度分别产生各个粒子新的位置.

Step3：随机产生一个n维、每个分量数值在0～1之间的向量.

Step4：当迭代次数k小于规定迭代次数，执行Step5，否则输出结果.

Step5：对于每一个粒子按照式（6），更新其速度，并限制速度的大小.

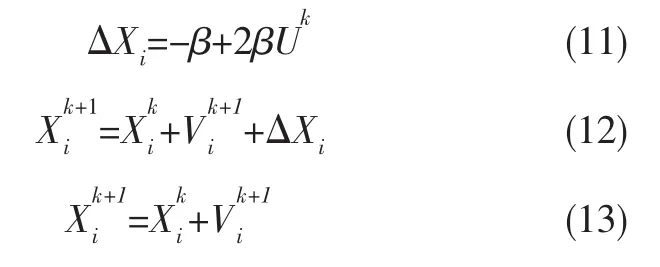
Step7：比较每个粒子新位置的适应值.对各个粒子的适应值和自身最优值pbest进行比较，如果当前适应值优于pbest，则将pbest置为当前适应值，对各个粒子的适应值和种群最优值gbest进行比较，如果当前适应值优于gbest，则将gbest置为粒子的当前适应值，转Step4.

该算法能够对基本粒子群进行改进，但当具体问题的最优解无法预知的情况下，扰动范围不易确定，对算法效果有较大的影响.作者针对这一问题进行研究，提出一个利用粒子间距离，自适应地改变扰动范围的算法.

4 距离启发信息

考虑到很多实际问题是一个多峰值问题，粒子群容易过早的进入收敛，落入局部最优.某个粒子与当前全局最优粒子的距离可用式（14）的σ2表示.

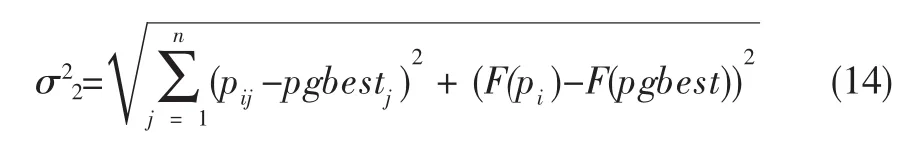
式中：pij是当前第i个粒子的第j维数值，pgbestj当前全局最优粒子的第j维数值，F为目标函数的表达式.与一般的距离公式不同，在式（14）中，既考虑了粒子与当前全局最优粒子之间的距离，又考虑了两者适应度的差异.

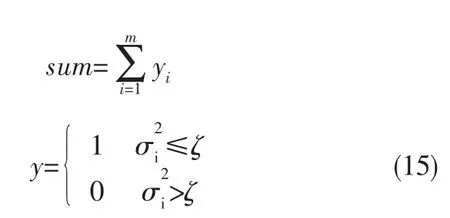
式（15）中的ζ为设定的阈值，m为粒子总数，当sum数值过多时，则意味着大量粒子都在当前最优值的周围，有可能落入局部最优，必须进行混沌扰动.作者提出了一种使用距离启发信息来确定扰动范围的方法，启发信息如下：

将上述混沌粒子群算法中的第6步式（11）改为式（17），就可以达到混沌扰动范围的自适应变动.

5 基于改进的自适应混沌粒子群算法选址

利用K-Medios方法结合改进后的混沌粒子群算法对式（5）进行求解.

5.1 改进的自适应混沌粒子群算法描述

算法描述如下：

输入：聚类个数k以及包含N个数据对象的样本集.输出：满足式（5）最小的k个聚类.

处理流程：

Step1：初始化.设定最大进化代数MaxT和当前进化代数，并置t=1，在问题空间利用混沌初始化产生M个粒子，组成初始种群X(t).

Step2：使用改进后的混沌粒子群算法进行寻优.

Step3：对新一代粒子进行K-Mediods优化.使用K-Mediods对新一代粒子划分的类进行聚类分析，确定每个粒子划分区域中的最佳中心点，并用其代替新粒子.

Step4：若达到最大代数或目标函数不再变化，则继续执行，否则转Step2.

Step5：输出最终的聚类结果.%%

新算法在产生下一代粒子时具有较大的遍历性，所以不容易产生局部极小值，对新一代个体的KMediods算法优化，更提高了收敛速度.由于不存在随机寻优的退化现象，因此后期收敛比较平稳，很少有波动现象.

5.2 最优解的判定

多目标优化问题在大多数情况下，各个目标函数间可能是冲突的.这就导致多目标优化问题不存在惟一的全局最优解，使所有目标函数同时最优.但是，可以存在这样的解：对一个或几个目标函数不可能进一步优化，而对其他目标函数不至于劣化，这样的解称之为非劣最优解(Pareto optimal)，而将所有子目标函数最优解组合成的解称为多目标组合优化问题的理想解.为此，对于每一个粒子所取得的较优解与理想解的偏差τ作为算法的性能评价指标.在每一次迭代时所有粒子取得的解中对应于最小偏差τ的粮食应急点选址方案即为当前的最优解.

在粮食应急点选址中，仅需要考虑两个优化目标，粒子i所取得较优解和理想解的的偏差τi如式(18)所示：

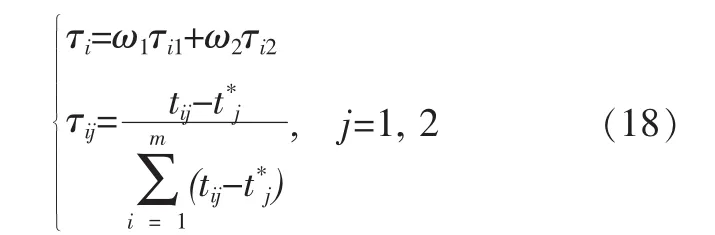
式中：ti1为粒子i选址方案中的最小总应急运输时间，ti2为方案中最小最迟应急时间.t*1为理想最小总应急运输时间，为理想最小最迟应急时间.

6 试验与结果分析

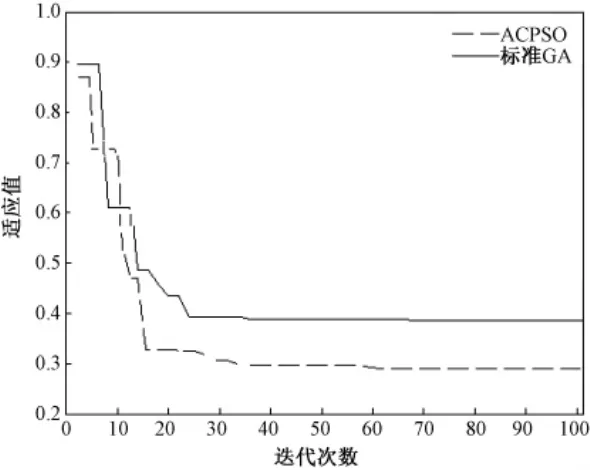
图1 两种算法的贴近度收敛情况

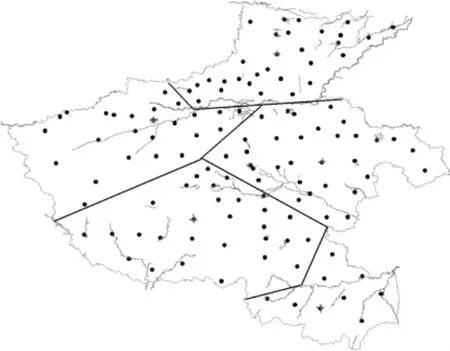
图2 使用ACPSO算法的求解结果

表1 应急点建设时间d

对河南省区域内的县级以上城市数据集分别采用遗传算法与改进的自适应混沌粒子群算法（ACPSO）进行试验和结果分析.考虑主要障碍物为黄河和淮河，聚类数目k=5，应急点最早开始使用时间(数据为归一化后的，县级市取其所在地级市时间，不另给出)见表1，ω1=0.9,ω2=0.1,λ取救援目标的人数与总人数的比值.

遗传算法的参数设置为：种群规模60，交叉概率0.8，变异概率0.05，迭代次数100代.粒子群参数设置：粒子个数60，最大迭代次数100，学习因子c1=c2=2, β=2，σ=0.001.

图1是两种算法的收敛曲线对比，由实验结果可以看出，ACPSO的试验结果具有较好的全局收敛性能，其收敛速度和收敛精度都较标准GA更好.图2给出了使用ACPSO算法求解的最优结果.

7 结束语

主要对一定区域下带障碍约束的粮食应急点选址进行了研究，结合粮食应急的自身特点，建立了该问题的多目标优化数学模型.针对传统算法对初始值敏感和容易陷入局部极值的缺点，研究并提出了一种自适应混沌粒子群算法.结果表明，该算法较好地解决了粮食应急点选址问题.本算法使用了混沌系统对粒子群进行初始化和扰动，因此如何选取更佳的混沌系统使其更进一步优化粒子群算法，是下一步进行研究的方向.

［1］ 何建敏,刘春林,曹杰,等.应急管理与应急系［M］.北京:科学出版社,2005:54-55.

［2］ Kennedy J,Eberhart R.Particle swarm optimization［C］//Proc of IEEE International Conference on Neural Networks,1995:1942-1948.

［3］ Clerc M,Kennedy J.The particle swarm-explosion,stability,and convergence in a multidimensional complex space［J］.IEEE Trans on Evolutionary Computation,2002,6(1):58-73.

［4］ Sun J,Feng B,Xu W B.Particle swans optimization with particles having quantum behavior［C］// IEEE Congresson EvolutionaryComputation, 2004:325-331.

［5］ 唐贤伦,庄陵,李银国,等.基于粒子群优化和模糊c均值聚类的入侵检测［J］.计算机工程,2008,34 (4):13-15.

［6］ 田东平.基于Tent混沌序列的粒子群优化算法［J］.计算机工程,2010,36(4):180-182.

RESEARCH ON SITE SELECTION OF GRAIN EMERGENCY SUPPLY LOCATION BASED ON SELF-ADAPTIVE CHAOS PARTICLE SWARM OPTIMIZATION

XIAO Le1,2,WU Xiang-lin1,ZHANG Xue-ping2
(1.Department.of Control Engineering,Huazhong University of Science and Technology,Wuhan 430074, China;2.School of Information Science and Engineering,Henan University of Technology,Zhengzhou 450001,China)

In order to solve the problem of site selection of grain emergency supply location,we established a corresponding optimization model to achieve the targets of the shortest transport time and the earliest emergency start time.We solved the model by use of a particle swarm-based k-medoids cluster algorithm,and we also put forward a self-adaptive chaos particle swarm optimization algorithm to avoid the solution from sinking to local optimum prematurely.The algorithm judged the current state of the particle swarm according to the Euclidean distance between particles and the known global optimum particle,and determined the chaos perturbation range by using the current state as the heuristic information so as to effectively improve accuracy of the optimal solution.The experiment showed that the algorithm was superior to the conventional evolutionary algorithm and could well solve the problem of site selection of grain emergency supply location.

grain emergency supply location;site selection;cluster;self-adaptive chaos particle swarm algorithm; distance heuristic information

TP311

A%%%%%%

1673-2383(2012)04-0077-05

http://www.cnki.net/kcms/detail/41.1378.N.20120829.1722.201204.77_018.html

网络出版时间：2012-08-29 05:22:00 PM

2012-03-08

“十一五”国家科技支撑计划重点项目(2008BADA8B03)；科技部科技型中小企业技术创新基金项目(10C26214102205)

肖乐(1972—)，男，河南开封人，副教授，博士研究生，研究方向为系统工程.