高压直流输电系统短路比在线估计
2012-09-19杨洪耕丁志林刘亚栋
刘 张,杨洪耕,丁志林,刘亚栋
(1.四川大学 电气信息学院,四川成都610065;2.四川省电力公司 超(特)高压运行检修公司,四川成都610041)
0 引言
高压直流输电系统中交流系统和直流系统之间的相互作用,很大程度上取决于交流系统相对于直流系统的强弱程度[1,2],该强弱程度可用短路比来衡量[3]。短路比为高压直流输电系统的规划和运行提供重要参考依据,当高压直流输电系统连于弱交流系统时,可能引发以下问题:高动态过电压、电压不稳定、谐波谐振和谐波不稳定、故障恢复的暂态过程不稳等[4~10],严重影响系统正常运行。因此,准确计算实时短路比,对于高压直流输电系统的运行具有重要意义,其中求解交流系统的短路容量是关键。
现有求短路容量的方法主要分为两类:一是根据换流站并联电容器 (或滤波器)投切时的无功变化量和交流母线暂态电压变化率的比值,可得到短路容量[11,12]。实际运行中,换流站的并联电容器 (或滤波器)投切动作不频繁,因此无法得到交流系统实时的短路容量。二是将交流系统进行等值简化处理,辨识其等值参数,通过等值阻抗可求出交流系统短路容量[13]。文献[14]利用本地测量值,用最小二乘法估计戴维南等值参数,但应用中遇到戴维南等值参数的漂移问题。为避免上述方法的不足,文献[15]提出采用平方根滤波器进行等值参数估计的方法。文献[16]分析了参数漂移的本质原因,通过预先对采样运行点进行筛选,可在一定程度上避免漂移问题,但实时性较差。文献[17]提出了基于偏差量修正的迭代算法,并用一致性检验对初值进行选择,但凭经验给出修正因子,计算结果受主观因素影响较大。
本文基于戴维南等值电路,提出一种利用独立随机矢量协方差特性的等值阻抗估计方法。为避免戴维南等值参数的漂移,根据交流侧电气量测量值,求取其均值和偏差,利用独立随机矢量协方差为零的特性[18,19]对阻抗解析式进行简化,并采用滑动数据窗在线计算得到等值阻抗,从而计算出交流系统的短路容量获得实时短路比。
1 基本原理
1.1 短路比
直流输电工程可看成换流站母线的一个可变负荷[20]。以送端交流系统为例,利用戴维南等值定理,将连接换流站的整个外部交流系统等值成理想电压源Vs和等值阻抗Zs的串联,换流站等值成可变负荷ZL,IL和VL分别是流经ZL的电流和端电压,如图1所示。
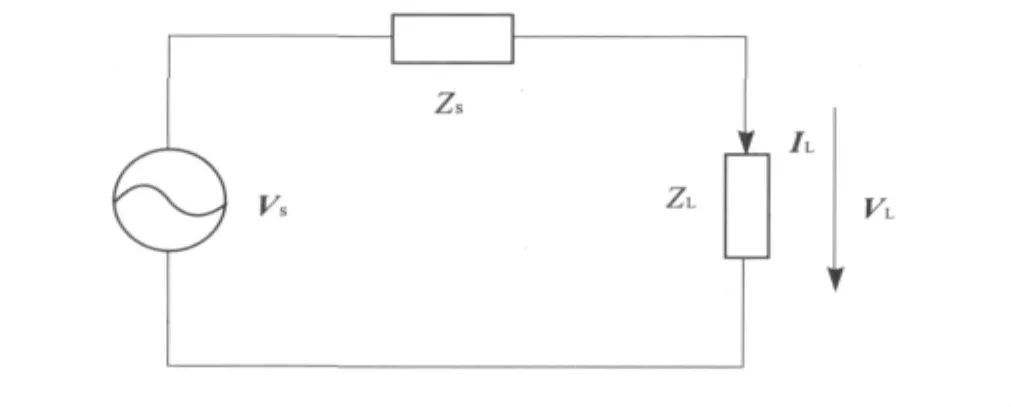
图1 高压直流系统戴维南等值电路Fig.1 Thevenin equivalent circuit of HVDC power system
定义交流系统短路容量Sac(MVA)和直流换流器额定功率PdN(MW)的比值为短路比 (Short Circuit Ratio):

交流系统短路容量Sac由式 (2)得出:

式中:VL为额定直流功率下的换相母线电压;Zs为交流系统的戴维南等值阻抗,没有考虑无功补偿设备 (如滤波器、并联电容器和调相机等)。
实际高压直流系统中,VL和PdN作为换流站的运行数据可直接获得。因此,可将求解SCR问题转化为求解Zs问题。
1.2 等值阻抗估计的解析式
根据图1,假设前一时刻t1的电压和电流分别为VL1和iL1,当前时刻t2的电压和电流分别为VL2和IL2,根据基尔霍夫电压定律可知:

t1~t2时刻,若戴维南参数恒定,系统侧电源未发生变化 (或者其变化可忽略不计),即Vs1=Vs2,由 (3)和 (4)式可得:
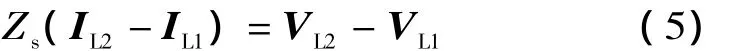
因此,等值阻抗Zs的数学表达如下:
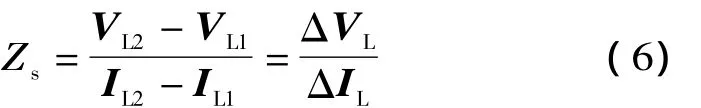
根据 (6)式的特点,Zs由电压和电流的波动量求得,本文暂且将该方法称为波动法。通过(6)式可得等值阻抗Zs,但实际计算中波动法会出现Zs漂移问题[14],导致计算结果误差较大,甚至出现明显错误。
为避免漂移问题,本文利用独立随机矢量协方差特性进行求解。由图1知,各时刻的测量值满足:
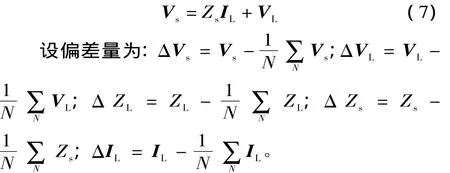
由 (7)式,各时刻的测量值和偏差满足:
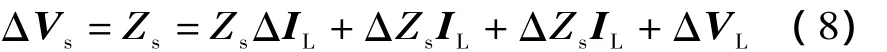
(8)式两端同时乘以ΔZ*L,对估计时段 (N个样本值)求和可得:
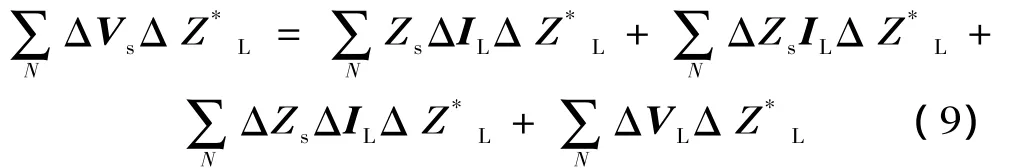
式中:*表示对复数求共轭。
负荷侧阻抗的变化和系统侧电源电压、等值阻抗无关,因此ΔZL分别和ΔVs,ΔZs相互独立。根据数理统计特性,两个独立随机矢量的协方差为0,实际计算中,若数据窗内样本点足够多,可得:
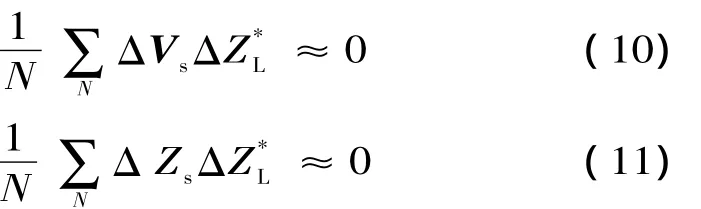
根据 (10)和 (11)式的近似处理,将 (9)式化简为:
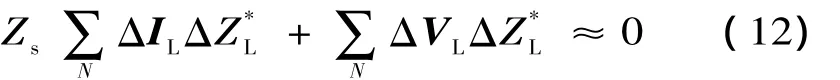
根据 (12)式,等值阻抗估算公式如下:
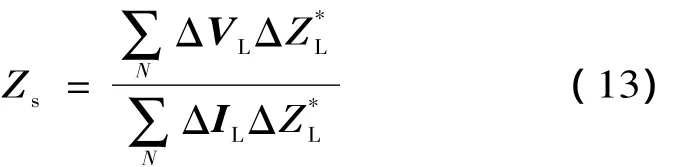
1.3 滑动数据窗模型
为实现在线估计,采用了随时间而滑动的数据窗在线计算等值阻抗。
以电流为例,滑动数据窗模型如图2所示。
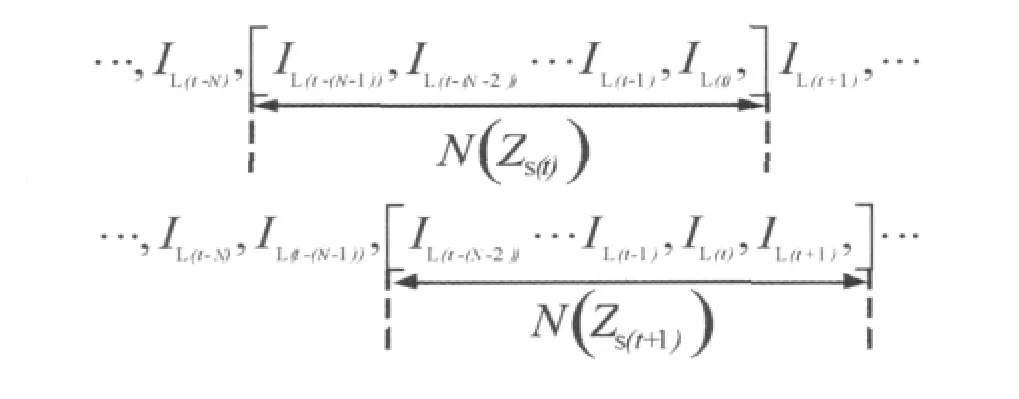
图2 滑动数据窗模型Fig.2 Sliding data window model
图2中,方框宽度N代表数据窗长度,即估计时段内的样本个数,当前时刻t对应的阻抗值为Zs(t)。在实时监控中,为计算t+1时刻的阻抗值Zs(t+1),可将数据窗N往右移一位,即放弃样本N中的第一个历史数据IL(t-(N-1)),同时将t+1时刻的电流值IL(t+1)加入数据窗中,窗口宽度仍保持N不变,重新计算可得Zs(t+1)。
2 仿真算例
本文以Matlab作为仿真工具,根据图1搭建试验仿真模型,等值电路参数假设如下:系统侧电压源幅值为200 V,初始相角为0;戴维南等值阻抗Zs幅值恒为2 Ω,相角恒为75°;等值负荷ZL幅值为20 Ω,相角为24°。仿真得到250个样本点,N=200,用本文方法与波动法计算的等值阻抗和准确值进行比较,结果如下:
(1)假设1:系统侧电压源±0.05%随机波动,等值负荷 ZL幅值 ±2% 随机波动,相角±2%随机波动。根据 (6)和 (13)式计算得到等值阻抗估计值如图3所示。
从图3可以看出,假设1条件下波动法估计的Zs幅值有明显的误差,其值大部分在±50%内变化,且变化频繁,甚至有一些明显偏离准确值的错误值;波动法估计的Zs相角结果中出现0到180°之间的值,表明此时估计的Zs为容性的,与准确值为感性阻抗明显不符,因此这些点的估计值明显是错误的,具体分析如表1。而用本文方法估计的结果与真实值更接近,而且相比于波动法较为平稳。
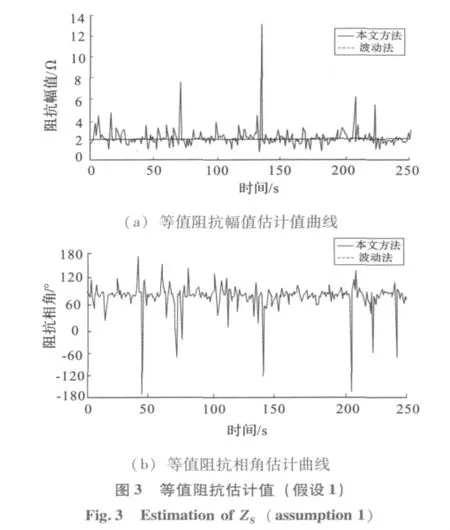
当t1和t2连续两时刻的负荷水平很接近,即△VL和△iL都趋于0,此时等式 (6)右边的式子将会趋近于0/0的模式。以假设1条件下的仿真为例,取图3中4个峰值点加以分析可以验证以上的结论,如表1所示。
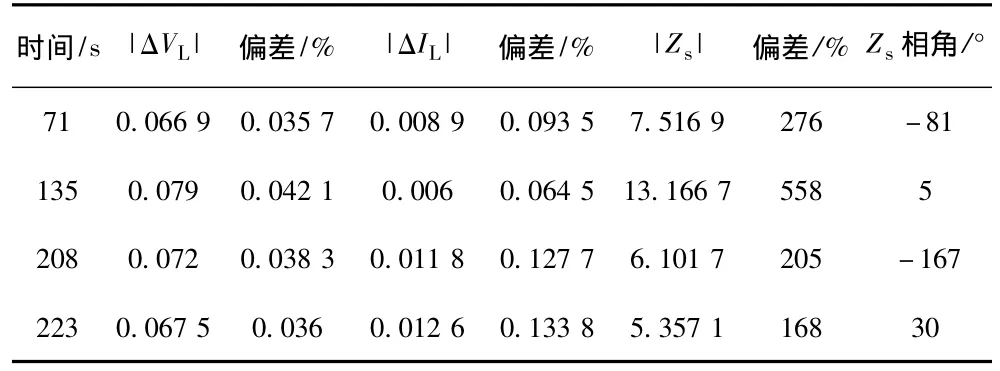
表1 峰值点分析Tab.1 Analysis of the peak points
(2)假设2:系统侧电压源±0.05%随机波动,等值负荷ZL幅值 ±15% 随机波动,相角±15%随机波动。根据 (6)和 (13)式计算得到等值阻抗估计值如图4所示。
对图3和图4分析可得,波动法估计结果的误差和变化情况受负荷波动情况的影响,当负荷波动较为剧烈时,估计结果误差小且变化小。但是无论负荷的波动情况如何,本文方法都能得到较为准确和稳定的估计值。
(3)假设3:系统侧电压源±1% 随机波动,等值负荷ZL幅值±15% 随机波动,相角±15%随机波动。根据 (13)式计算得到等值阻抗估计值如图5所示。
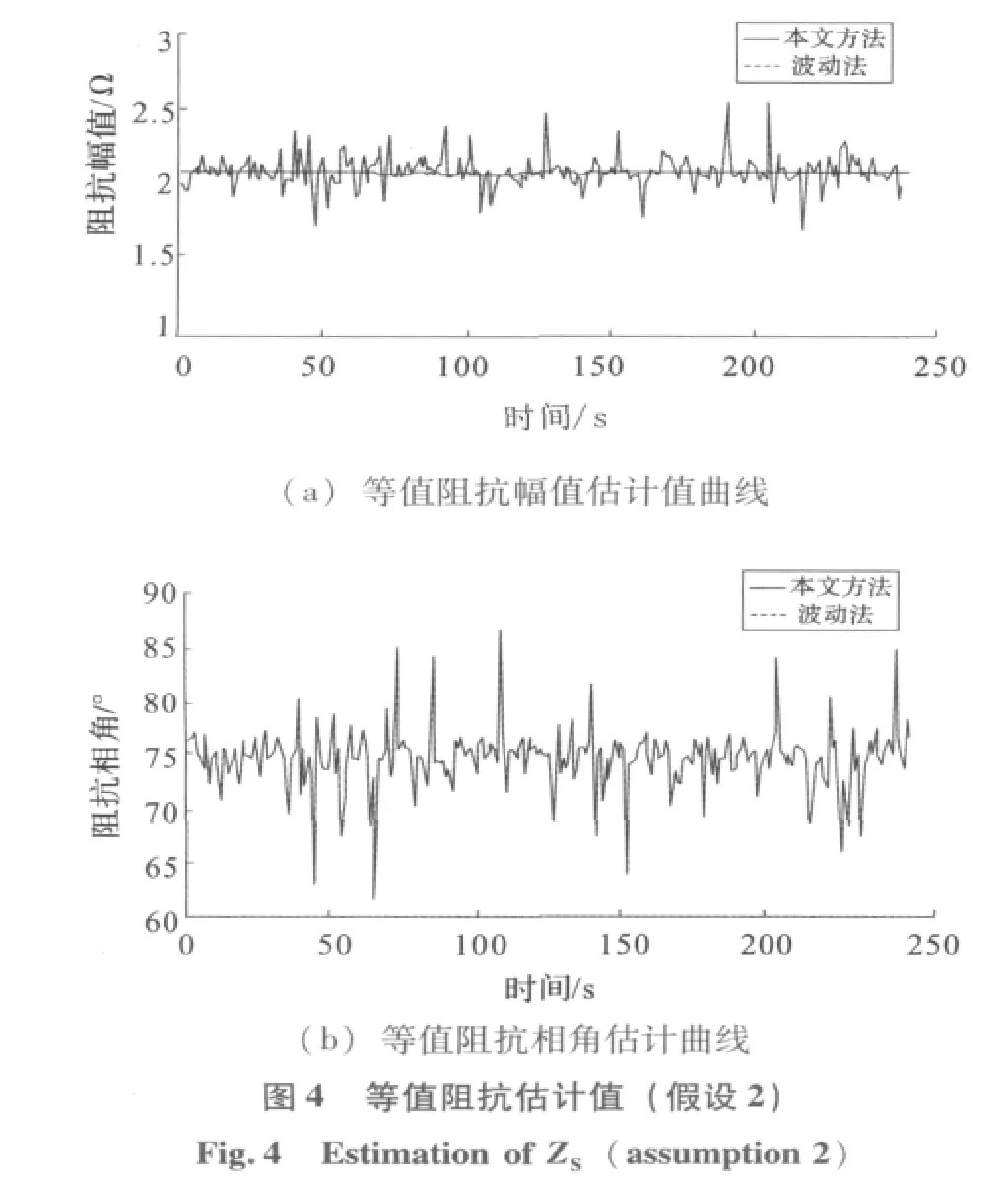
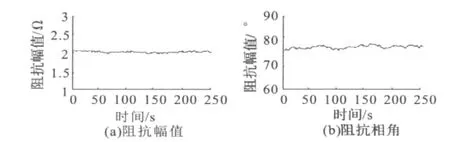
图5 等值阻抗估计值 (假设3)Fig.5 Estimation of ZS(assumption 3)
假设3条件下系统侧电压源的波动不能忽略,此时无法根据 (3)和 (4)式推导出 (6)式,即波动法此时不成立,可见波动法适用范围具有一定局限性。对于系统侧和负荷侧都变动的情况下,本文方法同样适用,且估计结果较为准确、稳定。
3 实际工程应用
本文用德阳-宝鸡±500 kV直流输电工程德阳换流站电气量实测值,对本文提出的方法进行验证分析。该高压直流输电工程交流侧母线额定电压525 kV,额定直流电压±500 kV,额定输电容量为双极3 000 MW,由调度提供的交流系统短路容量为3×104MVA左右。
验证数据为2010年10月1日00∶00~10月4日00∶00时段德阳换流站电气量实测值,如图6~图8所示。数据采样周期是5分钟,数据窗长度N=288。
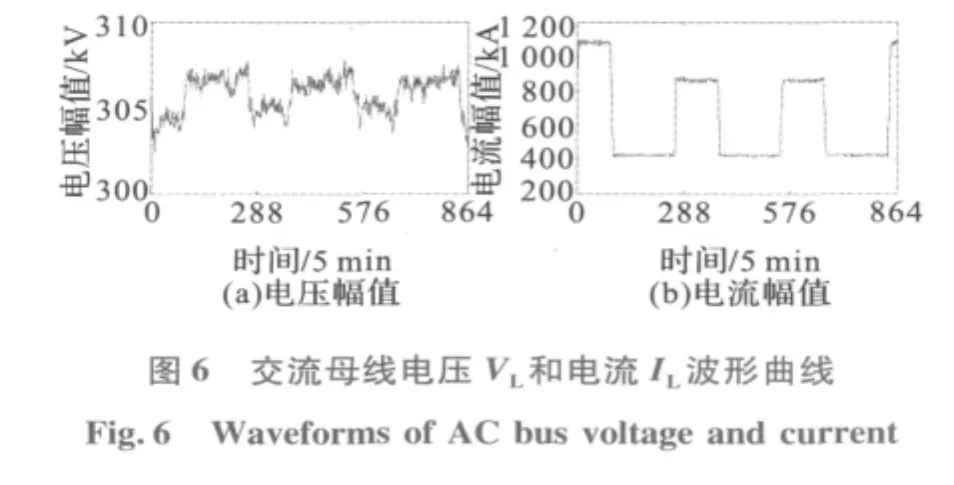
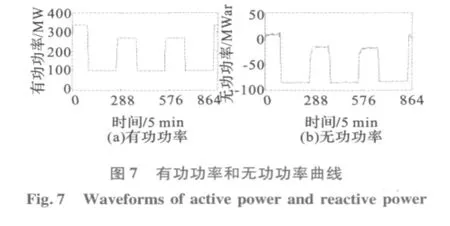
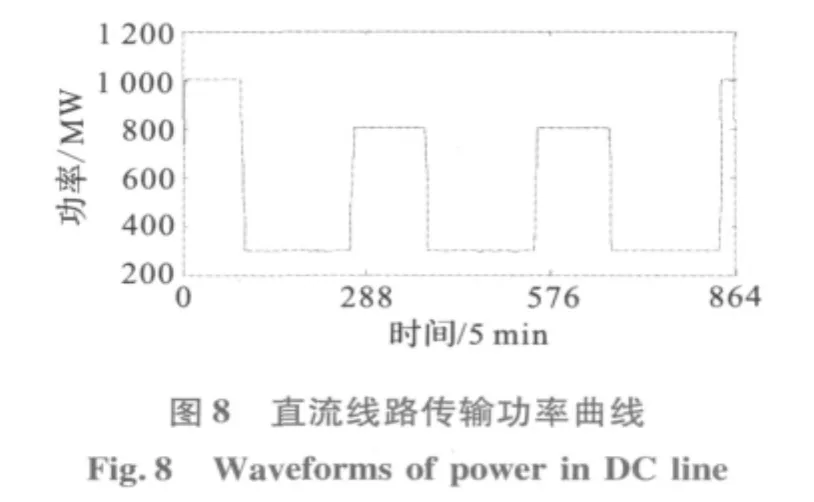
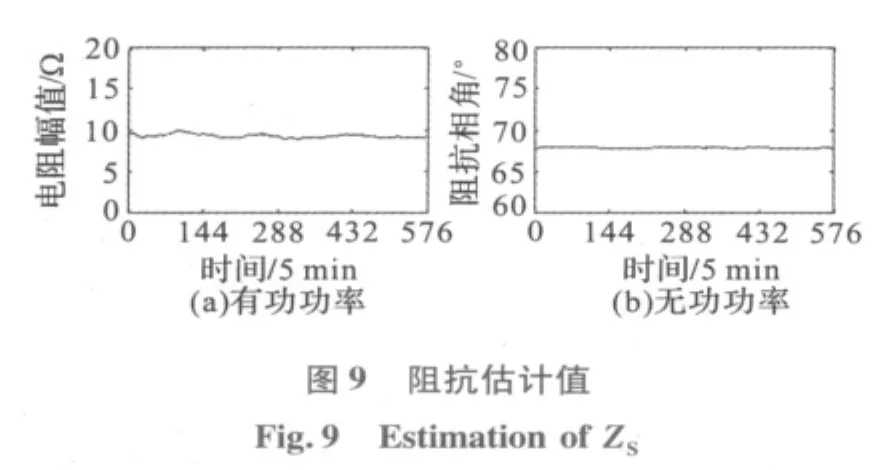
根据图6~图8的数据,利用本文方法计算的等值阻抗如图9所示,根据等值阻抗值计算的短路容量如图10(a)所示。
从图9可以看出,等值阻抗的幅值为9 Ω左右,相角为68°左右,短路容量为3×104MVA左右,与调度提供的值基本一致,满足工程计算要求,因此认为本文估计方法具有一定的正确性。
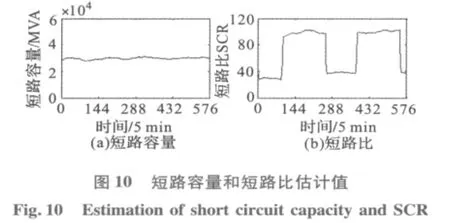
根据SCR计算式 (1),利用图8和图9数据计算得到短路比实时值如图10(b)所示,此时交流系统属于强交流系统[2]。
4 结论
(1)本文对高压直流系统交流侧进行戴维南等值,利用独立随机矢量协方差的特性简化等值阻抗解析式,采用滑动数据窗在线计算得到等值阻抗。根据等值阻抗计算得到短路容量从而得到实时短路比。
(2)本文验证使用的数据由换流站提供,时间间隔是5 min,实际应用中,为了更好地体现实时性,可将时间间隔缩短为30 s。
[1]KUNDER P.Power system stability and control[M]. 北京:中国电力出版社,2002.
[2]李兴源.高压直流输电系统的运行和控制[M].北京:科学出版社,1998.
[3]Gavrilovic A.AC/DC system strength as indicated by short circuit ratios[C].IEEE Conference on AC and DC Power Transmission,London,1991-09.
[4]Bodger P S,Irwin G D,Woddford D A.Controlling harmonic instability of HVDC links connected to weak AC systems[J].IEEE Trans on Power Delivery,1990,5(4):2039-2046.
[5]Thallam R S.Review of the design and performance features of HVDC systems connected to low short circuit ratio AC systems[J].IEEE Trans on Power Delivery,1992,7(4):2065-2073.
[6]魏星.交流系统强度对HVDC故障恢复特性影响的仿真分析[J].电力科学与工程,2007,23(3):24-26.Wei Xing.Simulation analysis of AC system strength on HVDC fault restoration characteristics[J].Electric Power Science and Engineering,2007,23(3):24-26.
[7]许德操,董凌,张晓阳,等.青海电网HVDC辅助频率控制研究[J].电网与清洁能源,2011,27(4):8-10.Xu Decao,Dong Ling,Zhang Xiaoyang,et al.Auxiliary frequency controller of Qinghai Grid's HVDC Link[J].Power System and Clean Energy,2011,27(4):8-10.
[8]穆子龙,李兴源.交、直流输电系统相互影响引起的谐波不稳定问题[J].电力系统自动化,2009,33(2):96-100.Mu Zilong,Li Xingyuan.Harmonic instability caused by interactions between AC and DC transmission systems[J].Automation of Electric Power Systems,2009,33(2):96-100.
[9]黄峰,杨洪耕.基于快速傅里叶变换的谐波和间谐波检测修正算法[J].电网与清洁能源,2010,26(6):28-32.Huang Feng,Yang Honggeng.A modified algorithm based on fast Fourier transform for Harmonics and interharmonics detection[J].Power System and Clean Energy,2010,26(6):28-32.
[10]Krishayya P C S,Adapa R,Holm M,et al.IEEE guide for planning DC links terminating at AC locations having low short-circuit capacities.France:CIGRE,1997.
[11]浙江大学发电教研组直流输电科研组.直流输电[M].北京:电力工业出版社,1982.
[12]杜忠明.贵广第二回直流输电工程换流站无功补偿的研究[J].电网技术,2006,30(10):69-74.Du Zhongming.Study on reactive power compensation for the secondary HVDC project from Guizhou to Guangdong[J].PowerSystem Technology,2006, 30(10):69-74.
[13]邓桂平,孙元章,徐箭.一种考虑母线短路容量的电压稳定解析方法[J].电力系统自动化,2009,33(8):15-19.Deng Guiping,Sun Yuanzhang,Xu Jian.A new voltage stability analysis method by considering short circuit capacity[J].Automation of Electric Power Systems,2009,33(8):15-19.
[14]朱绍碧,姜纯,陈继军,等.基于实时等值阻抗的电压稳定性分析[J].电力科学与工程,2010,26(5):34-37.Zhu Shaobi,Jiang Chun,Chen Jijun,et al.Analysis of power voltage stability based on equivalent impedance in real time[J].Electric Power Science and Engineering,2010,26(5):34-37.
[15]闫常友,刘建飞,杨奇逊,等.基于平方根滤波的网络等值算法[J].继电器,2006,34(3):41-46.Yan Changyou,Liu Jianfei,Yang Qixun,et al.Research on real-time equivalent based on square-root algorithm[J].Relay,2006,34(3):41-46.
[16]李来福,于继来,柳焯.戴维南等值参数的漂移问题研究[J].中国电机工程学报[J],2005,25(20):1-5.Li Laifu,Yu Jilai,Liu Zhuo.Research on parameters drift problem in tracking Thevenin equivalent[J].Proceedings of the CSEE,2005,25(20):1-5.
[17]牟散科,丁涛,顾伟,等.基于偏差校正的戴维南等值参数在线跟踪改进算法[J].电力系统保护与控制,2011,39(2):23-28.Mou Sanke,Ding Tao,Gu Wei,et al.An improved algorithm for on-line tracking thevenin equivalent parameters based on deviation correction[J].Power System Protection and Control,2011,39(2):23-28.
[18]罗鹏飞,张文明.随机信号分析与处理[M].北京:清华大学出版社,2006.
[19]刘晓石,陈鸿建,何腊梅.概率论与数理统计[M].北京:科学出版社,2005.
[20]徐政.联于弱交流系统的直流输电特性研究之二:控制方式与电压稳定性[J].电网技术,1997,21(3):1-4.Xu Zheng.The characteristics of HVDC system to weak AC systems PartII:control modes and voltage stability[J].Power System Technology,1997,21(3):1-4.
