双轴连续旋转的光纤陀螺捷联惯导误差分析

柳 明 ，王海军 ，常国宾

（1山东省高校航空信息与控制技术重点实验室（滨州学院），滨州256603；2滨州学院航空信息技术研发中心，滨州256603；3海军工程大学电气与信息工程学院，武汉430033）

1 引言

在惯性导航领域的相关研究中，捷联惯导的自补偿技术一直是研究的热点。惯导自补偿技术是指为了改变元件的工作方式而人为地引入某种运动，此运动的效果相当于通讯系统中的幅值调制技术，慢变的元件误差被调制后，在导航系统的解算过程中通过积分被减弱，从而使系统精度得到提高[1]。自补偿技术分为两种，一种为元件级自补偿技术，如美国弹道导弹战略核潜艇上装备的静电陀螺导航系统所采用的陀螺壳体翻转技术就属于此类；另一种为系统级旋转自补偿技术，该技术是通过对整个惯性测量组件施加人为的运动来达到对元件误差进行补偿的效果。系统级旋转自补偿技术于上世纪60年代提出，80年代该方法应用于西方的惯导系统中[2，3]。

光纤陀螺基于Sagnac效应通过测量光程差来测量角速度，是一种无运动部件的新型固态惯性元件，具有高可靠性的先天优势。同时光纤陀螺还具有低能耗、启动时间短、测量范围广、成本低等优点。由于光纤陀螺没有力矩器，若要进行元件级自补偿，则需要为陀螺外加旋转壳体，且需要4个陀螺，成本将增加。所以光纤陀螺导航系统一般采用系统级旋转自补偿技术。

美国研制用于战略核潜艇的新一代光纤陀螺导航仪即采用了系统级旋转自补偿技术。该系统采用当地地理坐标系编排，在跟踪地理水平的基础上引入双轴连续旋转技术来抑制元件低频误差的影响，同时在天向轴隔离地球自转和载体运动的影响，从而减小元件刻度系数不稳定性带来的系统误差。该系统设计目的是为了替代现役的静电陀螺导航系统，精度非常高[4，5]。

但上述系统机械结构非常复杂，成本昂贵。为降低成本，适于战术级应用的导航系统，本文将双轴连续旋转思想引入捷联惯导系统，并为安装方便改变了对旋转轴的选择。

2 双轴连续旋转方案

光纤陀螺惯导系统由相互正交的3个光纤陀螺仪和3个石英挠性加速度计组成。为了进行双轴旋转，将光纤陀螺惯导系统装在一个双环框架中。其中，外环轴与垂直于基座，内环轴位于垂直于外环轴的平面内。

下面定义本文中用到的主要坐标系：

（1）惯性坐标系i：用OXiYiZi表示，原点在地球中心且不随地球旋转，Xi、Yi轴在地球赤道平面内相互垂直并指向相应的恒星，Zi轴与地球的自转角速度向量重合。

（2）导航坐标系n：用OXnYnZn表示，它是惯导系统在求解导航参数时所采用的参考坐标系，本文选用地理坐标系作为导航坐标系。

（3）载体坐标系b：用OXbYbZb表示，原点在载体的质心上，Xb轴沿载体横轴向右，Yb沿载体纵轴向前，Zb垂直平面且向上。

（4）外环坐标系w：用OXwYwZw表示，Xw轴为内环轴，Zw轴与载体系的Zb轴重合。

（5）光纤陀螺惯导系统坐标系p：初始时刻p系和外环坐标系w系重合，各轴定义同外环坐标系。

由系统的旋转方式可知，p系相对w系绕Xw轴以角速度ω连续旋转、w系相对b系绕Zb轴以角速度ω/3连续旋转，其坐标旋转图见图1。

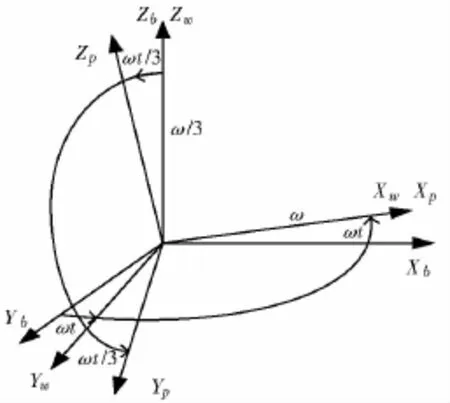
图1 坐标旋转示意图

则w系到p系的方向余弦矩阵）、b系到w系的方向余弦矩阵（t）、b系到p系的方向余弦矩阵（t）可根据方向余弦的定义很容易写出，本文不再赘述。

光纤陀螺惯导系统绕内环轴以角速度ω连续旋转，同时内环框架和光纤陀螺惯导系统一起绕外环轴以角速度ω/3连续旋转，光纤陀螺惯导系统绕内环旋转6周后以相同速度、相反方向继续连续旋转，与此相同，绕外环轴的旋转在旋转2周后改变方向，以此不停地进行下去，为了达到更好的调制效果，两旋转的转向不应同时发生。

内、外环旋转不采取相同转速的原因为：若采用相同的转速，任何一个元件其敏感轴的轨迹在空间中为一个圆周，旋转的结果和单轴旋转相同，而单轴旋转式捷联系统即使对常值误差也不能起到完全调制的作用。

3 双轴连续旋转式惯导误差分析

旋转调制式捷联惯导的误差传播方程为：

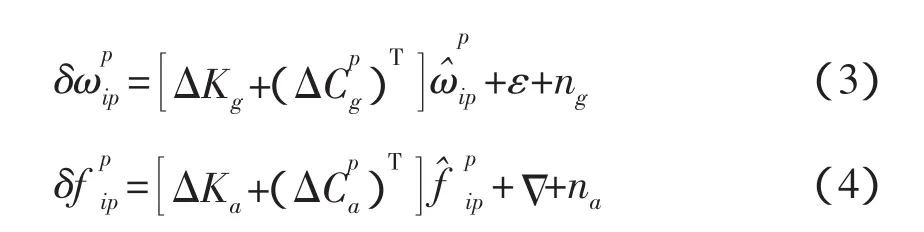
式中，ΔKg、Δ、ε、ng分别为陀螺仪的刻度系数误差、安装误差、常值漂移和随机噪声；ΔKa、Δ、Δ、na分别为加速度计的刻度系数误差、安装误差、常值零偏和随机噪声。

上述各误差均为标定后的剩余误差，如ΔKg应为陀螺仪刻度系数不稳定度引起的误差。

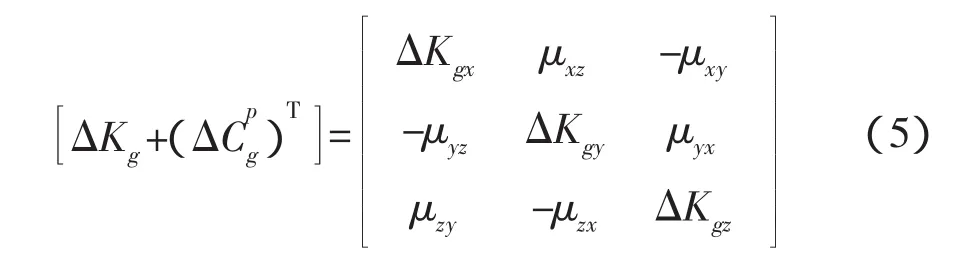
以陀螺仪组件为例，其输出误差在载体坐标系里的等效误差为：

式（6）前两项由安装误差和刻度系数误差引起，并与载体的动态相关，当载体为静态时，对第一项展开，并在时间轴上求平均可得式（7）。

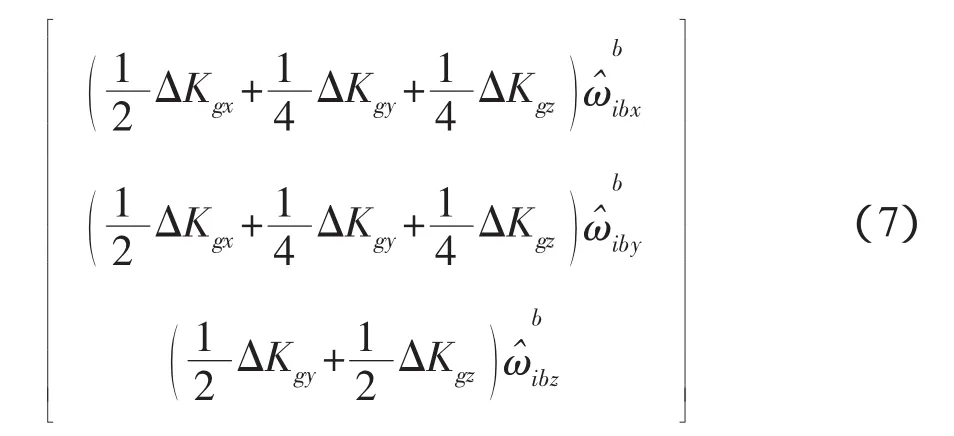
由此式可知，即使在静态（相对当地地理坐标系）条件下，此项误差也不能被完全调制，当载体为动态（即不为常值）时，刻度系数误差、安装误差引起的陀螺等效误差将在载体系各轴之间产生耦合，调制效果将进一步下降。

对式（6）第二项展开并在时间轴上求平均可得式（8）。

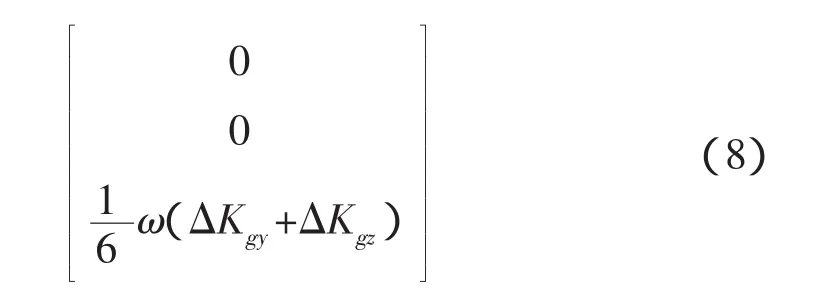
由此式可知，旋转调制角速度会和IMU坐标系y轴和z轴上的陀螺刻度系数误差产生耦合，但由于调制角速度ω的方向周期性地改变，经积分后此项误差可以被消除。若不采用定期反向措施，假如陀螺仪有10ppm的刻度系数误差，调制角速度为每分钟一转，则此项误差可达0.07deg/h的等效陀螺漂移误差，此误差将淹没旋转调制对陀螺仪常值漂移的补偿作用。

对式（6）前两项误差的分析可知，双轴连续旋转对刻度系数不稳定性和安装误差有一定的补偿效果，但不明显，特别是在动态条件下，此误差对系统影响更大。

式（6）第三项为陀螺常值漂移引起的载体系内等效陀螺漂移：

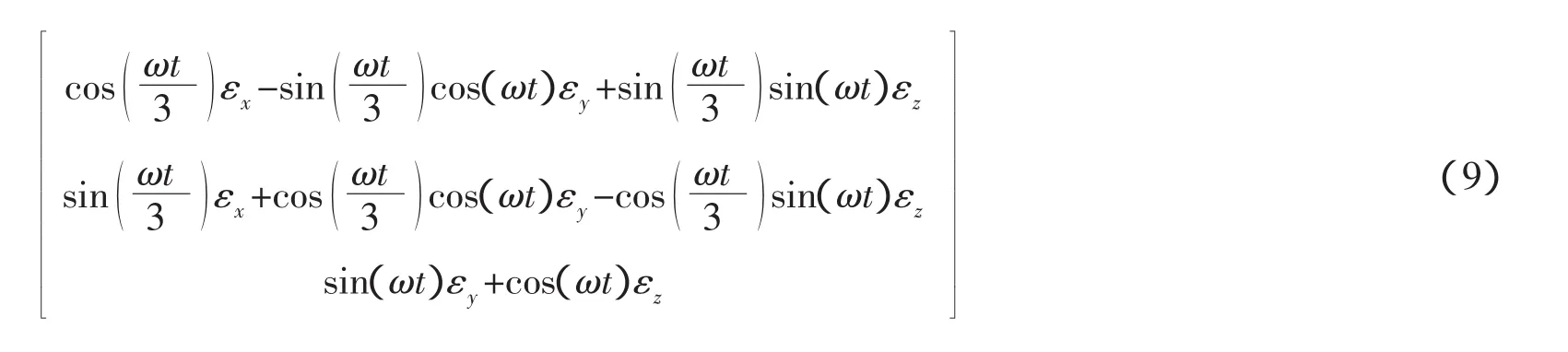
在时间轴上取平均后，此项误差为0，说明双轴连续旋转调制对常值漂移具有完美的调制效果。不难得出，元件的慢变漂移误差具有与常值误差相似的结论。

第四项为陀螺随机漂移角速率引起的载体系等效陀螺漂移，求其方差阵，并在时间轴上求平均可得：

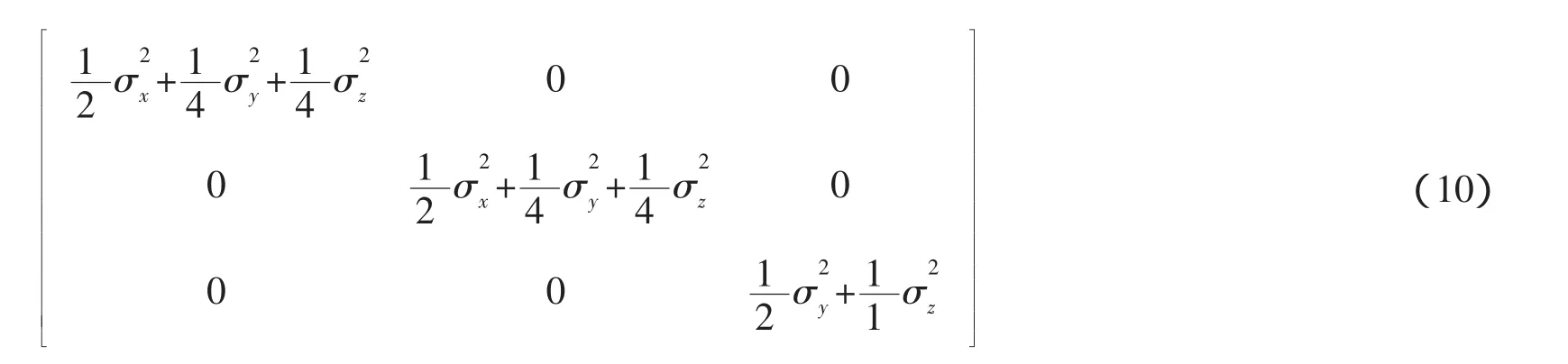
由上式可知，双轴连续旋转调制对陀螺随机漂移引起的误差没有补偿效果。

4 仿真分析

为了验证上述分析结论，对传统无旋转捷联惯性导航系统方案和本文所提出系统方案的误差传播方程进行了数字仿真试验，试验分为四部分，分别为总体试验、仅存在常值误差时的试验、仅存在刻度系数误差和安装误差时的试验、仅存在随机误差时的试验，对于每次试验，分别选取纵摇角误差、航向误差和经度误差三项指标对两个系统的性能进行比较。

4.1 仿真条件

仿真中，真实的横、纵摇角、航向角分别为：θ（t）=3°sin（πt/3）、φ（t）=5°sin（πt/6）、φ（t）=0.5°sin（πt/4）。

三个陀螺的常值漂移为0.01（°）/h，随机白噪声标准差为0.01（°）/h，标度因素误差为，陀螺组件的六个安装误差均为20″；三个加速度计的零漂均为0.5mg，随机白噪声的标准差为0.2mg，标度因数误差为10-4，加速度计组件的六个安装误差均为20″；初始纬度为45°，仿真时间为36h，仿真步长为1s；对于双轴旋转调制系统，旋转速度ω=π/30。

4.2 仿真结果

仿真结果中每幅图的上面一组为传统方案的误差，下面一组为本文方案的误差。

通过图2中的仿真曲线可以看出，双轴连续旋转方案可以有效地提高系统的精度，特别是系统的经度精度，在动态条件下可以提高近一个数量级。由图3、图4和图5中的仿真曲线可以知道，系统旋转自补偿技术主要作用是显著地减弱了元件常值误差对系统的影响，元件刻度系数误差和安装误差引起的系统误差没有减小，元件输出中包含的随机误差（主要是白噪声）引起的系统误差在旋转的作用下没有得到抑制。

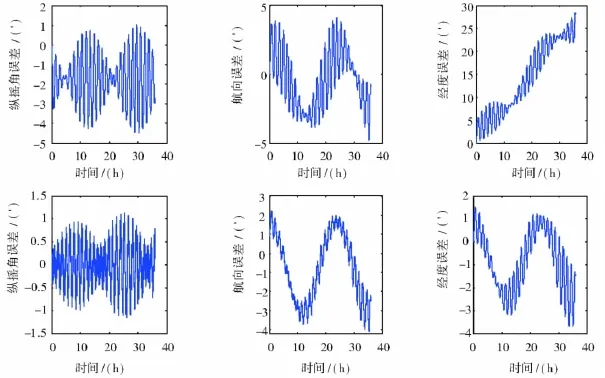
图2 总体误差

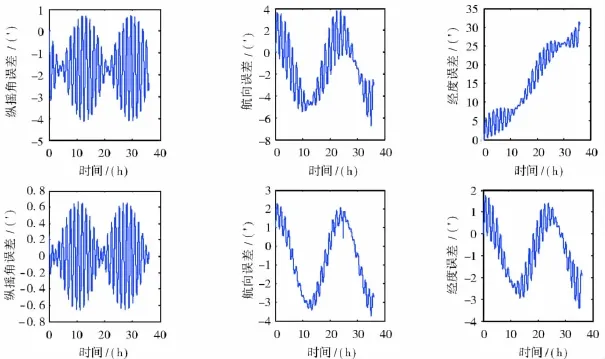
图3 仅存在元件常值误差时误差

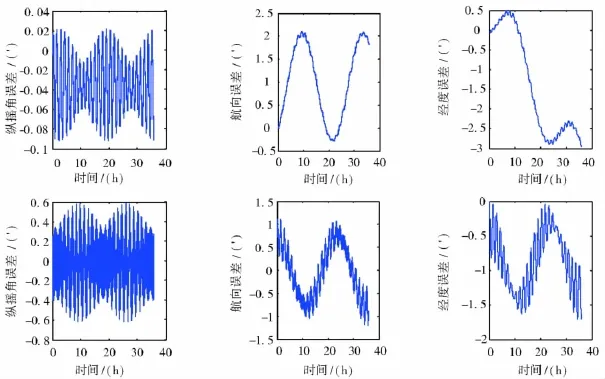
图4 仅存在安装和刻度误差时误差

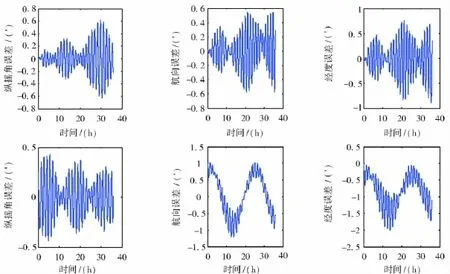
图5 仅存在元件随机误差时误差

5 结论

对双轴连续旋转调制式捷联惯导的旋转方式进行了阐述，通过分析系统误差传播方程，解释了该方案对系统进行误差补偿的机理。并通过数字仿真试验对理论分析进行了验证。

对于元件常值误差，该方案有非常明显的补偿效果，这说明在研制旋转调制式捷联惯导时，可以适当放宽对元件常值误差指标的要求。对于安装误差和刻度系数不稳定性造成的系统误差，该旋转调制方案的补偿效果不明显。光纤陀螺的输出随机噪声对应于陀螺仪的角度随机游走系数，本文的研究发现，这项误差不能被旋转调制补偿掉。◇

［1］Lahham J，Wigent D，Coleman A.Tuned support structure for structure-borne noise reduction of inertial navigator with dithered ring laser gyros［C］.Proceedings of the IEEE Position Location and Navigation Symposium，2000:419-428.

［2］Morrow R，Heckman D.High precision IFOG insertion into the strategic submarine navigation system ［C］.Position Location and Navigation Symposium，IEEE 1998 20-23 April 1998 Page（s）:332-338.

［3］LU Zhi-dong，WANG Xiao-bin.Error analysis and calibration of systematic dual-axis rotation-modulating SINS ［J］.Journal of Chinese Inertial Technology，2009，17（1）:8-14.

［4］王其，徐晓苏.旋转IMU在光纤捷联航姿系统中的应用［J］.中国惯性技术学报，2007，15（3）:265-268.

［5］翁海娜，陆全聪，黄昆，等.旋转式光学陀螺捷联惯导系统的旋转方案设计［J］.中国惯性技术学报，2009，17（1）:8-14.