新型短波信道探测序列研究

刘月亮 蒋宇中 姜 伟

（海军工程大学电子工程学院，湖北 武汉 430033）

引 言

短波通信具有通信距离远、设备简单、造价低廉、机动灵活、使用方便等优点，被广泛应用于远距离通信［1］。短波通信主要是靠电离层反射来实现的，而电离层的随机起伏变化导致回波信号十分微弱，需要有足够的相干积累提高信噪比［2］。在短波信道探测中，性能优越的探测序列，可以以较小的发射功率实现多径时延、多普勒频移等信道重要参数的高精度测量。所以，探测序列的选择与设计是一个非常关键的技术。因此，积极探索新型短波信道探测序列具有十分重要的意义。

在传统脉冲压缩体制中被用于相关检测的伪随机序列有最长线性移位寄存器序列（m序列）、巴克码等，主要依据序列的自相关特性来评估其检测性能［3］。近年来，恒包络零自相关（CAZAC）序列以其优越的周期自相关特性得到广泛重视和应用。CAZAC序列最早在20世纪50年代由Frank提出，并应用于Zadoff和Abotrezk研制的同步系统专利中［4］，但其长度仅限于N2（N 为整数）。1961年，Heimiller在文献［5］提出一种CAZAC序列，其长度也仅限于N2.1962年，Frank和Zadoff在文献［6］中对Frank早期提出的序列重新进行整理。1972年，D.Chu在Frank和Zadoff的基础上给出了一种任意长度的CAZAC序列［7］，即Zadoff-Chu序列。Zadoff-Chu序列的优良特性［8-9］主要有:恒包络特性，保证最佳的发射效率，且便于实现相干检测中的无偏估计；理想的周期自相关特性，自相关峰值尖锐；低峰均比特性，便于功率放大器的实现。

短波信道斜向探测主要利用探测序列良好的自相关特性进行相关检测。Zadoff-Chu序列的周期自相关函数（ACF）在理论上除了零点以外其余点都为零，因此，将该序列应用到短波信道探测中是一种有益的探索。为了更清晰地表明Zadoff-Chu序列性能的优越，将其与m序列和巴克码进行比较，通过仿真与实测进行验证。为简便，将Zadoff-Chu序列、m序列和巴克码统称为探测序列。

1.理论分析

1.1 探测序列的自相关特性

在短波信道探测时，如果一次只发送一个探测序列（a1a2…aN），由于传播存在延时，接收端接收到的信号形式是:噪声，a1a2…aN，噪声，就难以利用Zadoff-Chu序列的周期自相关特性。为充分利用Zadoff-Chu序列的周期自相关特性，将若干个（如L个）周期为N的相同序列连接成一个长度为L×N的新序列（a1a2…aN，a1a2…aN，…，a1a2…aN），则在接收端接收到的信号就为:噪声，a1a2…aN，a1a2…aN，…，a1a2…aN，噪声。在接收端相关检测时，从接收序列的起始位置开始，每移动一位，就依次取出N个值与发端序列的本地复制品做互相关运算，即是Zadoff-Chu序列的周期自相关。在相关运算之后，应该得到L个尖峰。

令L是一个大于零的正整数，k是任意一个与L互质的整数，则第k组周期为L的Zadoff-Chu序列的第n个值［10］为

式中:n=0，1，…，L-1；j表示虚数单位。当L是偶数时，Zadoff-Chu序列的周期ACF为

式中m=0，1，2，…，L-1.由式（2）可以看出，当m=0时，Corru［0］=L；当m=1，2，…，L-1时，因为k与L 互质，所以exp（j2πkm／L）是1的第L个初始根，有定理［5］知，［exp（j2πkm／L）］n=0.

目前最长的巴克码仅有13位，为使ACF的尖峰效果更明显，需要将巴克码进行扩展。以N位巴克码BarkN为例，其扩展算法［11］为:如果第i位的巴克码为x，则将x·BarkN作为新码组的第i个分组，最后组成N×N位扩展巴克码。

k=1，L=128时Zadoff-Chu序列、周期为127的m序列、长度为121的扩展巴克码与其三次重复序列的归一化互相关函数（CCF）的模如图1所示。

1.2 探测序列的调制与解调

Zadoff-Chu序列、m序列和巴克码三种探测序列都是宽带序列，在实际应用中由于受到短波信道探测收发信机带宽的限制，不能直接加以使用。为了能在信道中传输，需先通过插值将其频谱压缩，经成形滤波将插入值变成准确内插值。N倍内插是指在两个原始序列样点之间插入N-1个零值。包含信号90%能量的带宽B90%与比特率Rb的关系［12］为:B90%≈1.7Rb.在短波信道探测中，收发信机的带宽Bdt≈2.4kHz，信号带宽应控制在2.4kHz内，因此有

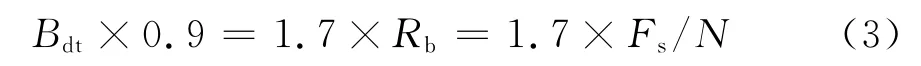
式中:Fs为采样频率；N为内插倍数。

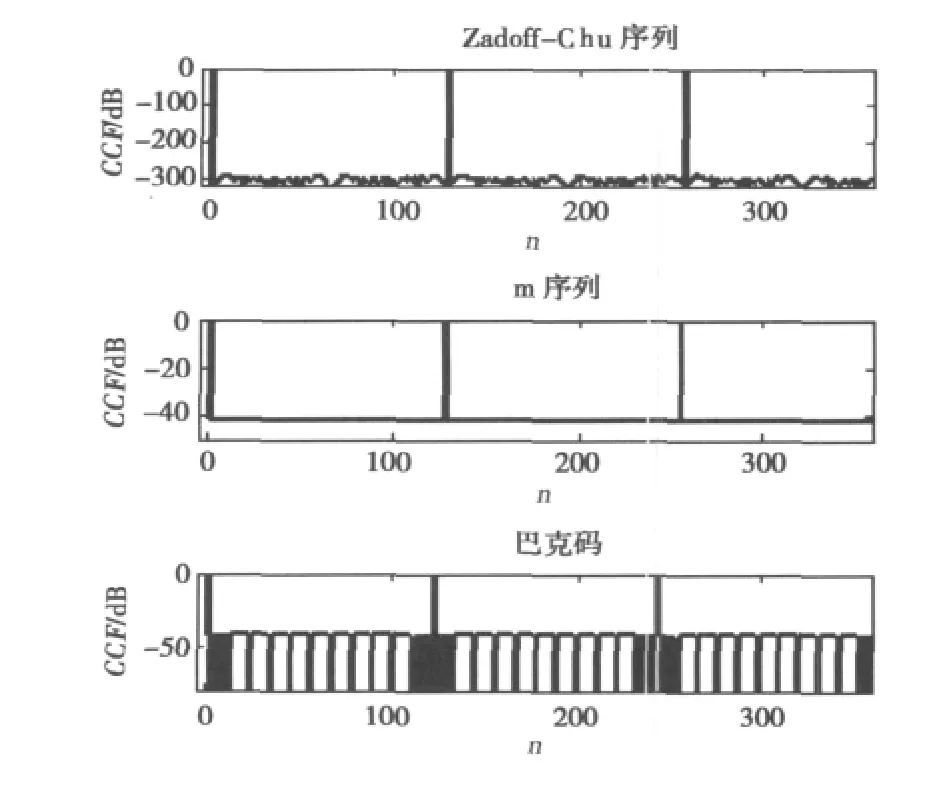
图1 探测序列与其重复序列的归一化CCF

在实际应用中，m序列和巴克码内插的值不是零，而是在两个原始序列样点之间插入N-1个与前一个原始序列样点相同的值。Zadoff-Chu序列的内插是在其生成公式中直接实现的。当L为偶数时Zadoff-Chu序列的N倍内插算式为

当L为奇数时Zadoff-Chu序列的N倍内插算式为

在式（4）和（5）中，n=0，1，…，LN-1，（n+1）／N为整数时保留了原序列的值，（n+1）／N不为整数时才是插入的值。内插的好处是插值后序列的频谱滚降更快，几乎无旁瓣，能量十分集中。

用有限长冲击响应（FIR）低通滤波器对Zadoff-Chu序列、m序列和巴克码内插后的序列进行成形滤波滤除其高频镜像后，其插入值变成准确内插值［13］。

能通过短波信道探测收发信机的信号频率大约在300～2700Hz范围内，为了充分利用这个有限的带宽，需将带宽为1.2kHz基带信号上变频到该频带内。由于Zadoff-Chu序列为复值序列，所以，实部和虚部要分别进行上变频，相加后进行数模变换，然后送入短波信道。设Zci［n］为Zadoff-Chu序列成形滤波之后的序列，zr［n］、zi［n］分别为实部和虚部上变频之后的序列，ZcM［n］为上变频之后实部和虚部的和序列。具体如式（6）所示。由于m序列和巴克码是实序列，上变频时直接与载波（2πfo（n-（L·N-1）／2）／Fs）相乘即可。

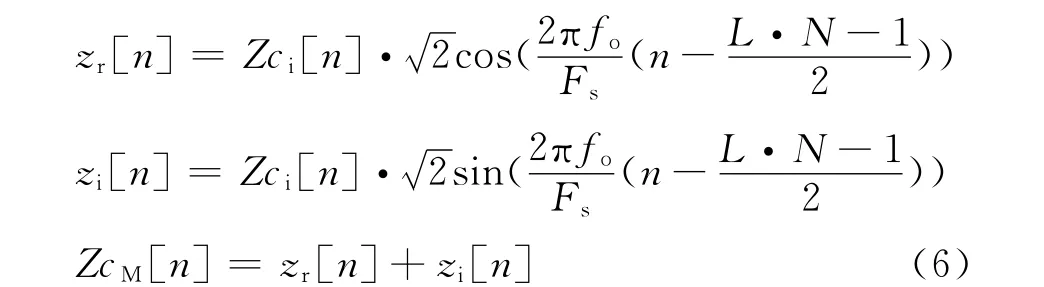
在接收端，为减小带外噪声，需先对接收信号进行带通滤波。序列的下变频是与上变频相反的过程。设Zadoff-Chu序列带通滤波之后的序列为ZcLP［n］，将其与两个相互正交的载波相乘之后的信号分别为uDr［n］、uDi［n］，它们合成的复序列为ZcD［n］，则有

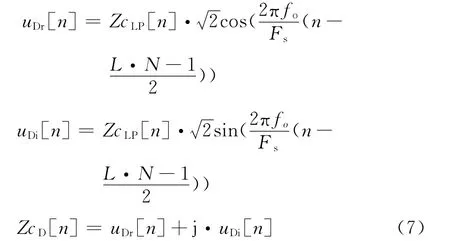
将序列ZcD［n］经与成形滤波器参数相同的FIR低通滤波器滤除二次谐波后即实现下变频。由于m序列和巴克码是实序列，直接将其与载波相乘，经FIR低通滤波器滤除二次谐波后即实现下变频。

离散时间信号的抽取包含信号抽样和尺度变换两个步骤，即先以抽样间隔N对离散时间信号进行抽样，然后再对抽样信号进行1／N的尺度压缩变换。对探测序列进行整数倍抽取后，将抽取得到的序列与其相应的发送序列的本地复制品做互相关，进行相关检测。

2.探测序列的性能仿真与实测分析

2.1 信号的评价指标

主旁瓣峰值比（PCM）［14］，定义为ACF的主瓣峰值与旁瓣最大值之比，即

品质因子（MF）［15］，定义式为

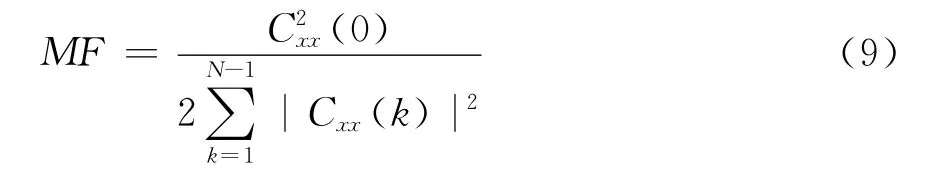
联合旁瓣电平率 （ISLR）［16］是ACF所有旁瓣的平方和与主瓣峰值的平方的比，定义式为

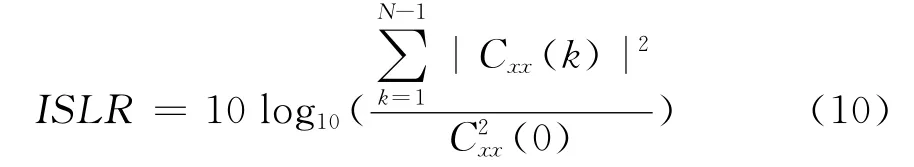
峰均功率比（PAPR）［17］，是信号平方的最大值与信号平方的均值之比，定义式为

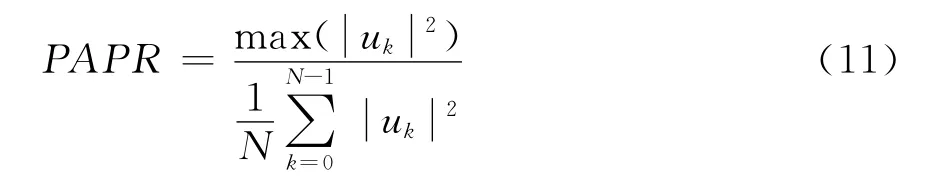
在式（8）、（9）、（10）中，Cxx（k）表示序列的 ACF，Cxx（0）表示序列ACF的主瓣峰值，max｛Cxx（k）｝k≠0表示序列ACF的旁瓣最大值。在式（11）中，uk表示信号，max表示求最大值。PCM、MF值越大越好，ISLR、PAPR值越小越好。

2.2 仿真与分析

仿真采用的数据是长度为3×128比特的Zadoff-Chu序列、长度为3×127比特的m序列和长度为3×121比特的巴克码。内插倍数取N=8，载波频率1.5kHz.FIR低通成形滤波器的参数为:通带带宽1.2kHz、截止频率1.5kHz、阻带衰减-70 dB、采样频率为8kHz，阶数为69.短波电台音频输出口输出的信号已是低频信号，在接收端用FIR低通滤波器代替带通滤波器。低通滤波器的参数为:通带带宽2.7kHz、截止频率3.0kHz、采样频率8 kHz、阻带衰减-80dB、阶数为31.

在接收端，将8倍抽取得到的序列与其相应的发送序列的本地复制品做互相关，其CCF如图2所示。从图中可以看出，三种探测序列的CCF都有较大的旁瓣，但相比之下，Zadoff-Chu序列CCF的旁瓣最小。

在发送端，Zadoff-Chu序列、m序列和巴克码上变频之后的信号的PAPR值分别为2.44、3.26、2.95.在理论上和接收端抽取后，三种探测序列CCF的PCM、MF、ISLR仿真值分别如表1和表2所示（这里所说的理论上的值是指不对探测序列做任何处理时的值）。

图2 抽取后的序列与发端探测序列的归一化CCF

表1 理论上序列ACF的PCM、MF、ISLR值

表2 抽取后序列CCF的PCM、MF、ISLR值

从表1可以看出，在理论上，Zadoff-Chu序列ACF的PCM、MF、ISLR值比m序列和巴克码的相应值优越很多。从表2可以看出，在接收端抽取后，Zadoff-Chu序列的CCF的PCM 值分别比m序列和巴克码的PCM 值提高6.3dB、13.1dB，MF值分别是m序列和巴克码的MF值的11倍和86倍，ISLR值分别比m序列和巴克码的ISLR值低10.4dB、19.3dB.这些表明Zadoff-Chu序列比m序列和巴克码具有更好的自相关特性。

对比表1和表2可以看出，抽取后探测序列CCF的PCM、MF、ISLR仿真值比其理论值有较大减小，这是对探测序列处理过程中的内插、上变频、下变频、抽取引起的数据精度下降所致。此外，三次滤波也是原因之一，因为所设计滤波器虽然是线性相位的，但对序列不同频率分量的相移不同。特别是Zadoff-Chu序列，对相位变化比较敏感，其抽取后的CCF的PCM、MF、ISLR值比其理论值大幅度减小。尽管如此，Zadoff-Chu序列的自相关特性仍然比m序列和巴克码的自相关特性好很多。

2.3 实测与分析

实验在自动扫频短波信道斜向探测系统平台上实现，该系统主要有数字信号处理（DSP）模块、复杂可编程逻辑器件（CPLD）时序控制模块、模数／数模转换（ADC／DAC）模块、电台工作模式和频率控制模块、全球定位系统（GPS）接收机模块、GPS导航电文接收模块、通用串行总线（USB）模块、时钟模块、锁相环（PLL）、计算机（PC）终端和短波电台组成，系统的收发同步由GPS秒脉冲触发实现，同步误差在10-9数量级，系统结构框图如图3所示。实验所用数据与仿真所用数据相同；收发信机为IC-725A型短波电台；短波电台工作频率为25MHz，收发双方载频差低于0.01Hz；调制方式为调幅（AM）；天线为伞形天线。

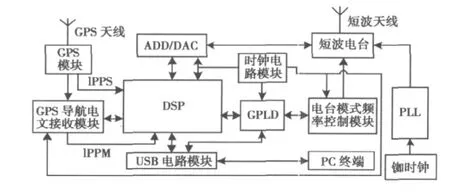
图3 自动扫频短波信道斜向探测系统框图

实测数据在接收端抽取后，Zadoff-Chu序列、m序列和巴克码三种序列与其发端相应序列的本地复制品的CCF如图4所示，CCF的PCM、MF、ISLR值如表3所示。

在图4中，三种探测序列的归一化相关函数的主瓣都有一定宽度。Zadoff-Chu序列的旁瓣几乎都在-30dB以下，幅度上下浮动较小，几乎没有较大的旁瓣凸出出来，这说明该序列具有很好的相关特性。m序列旁瓣也几乎都在-30dB以下，但其幅度上下浮动较大，特别是有个别旁瓣较大，在相关检测时容易造成误判。与Zadoff-Chu序列相比，m序列的相关特性稍差。巴克码旁瓣大概都在-20 dB以下，但其幅度上下浮动很大，而且较大的旁瓣很多，在相关检测时容易造成误判。与前两者相比，巴克码的相关特性较差。

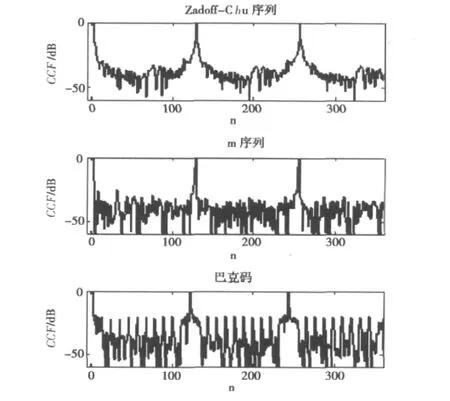
图4 实测抽取后的序列与发端探测序列的归一化CCF

表3 探测序列CCF的PCM、MF、ISLR实测值

从表3可以看出，Zadoff-Chu序列CCF的PCM值分别比m序列和巴克码的PCM值提高4.5dB、10.0dB，MF值分别是m序列和巴克码的MF值的4.9倍和5.4倍，ISLR值分别比m序列和巴克码的ISLR值低6.89dB、7.30dB.这说明Zadoff-Chu序列比m序列和巴克码具有更好的自相关特性。

对比表2和表3可以看出，探测序列CCF的PCM、MF、ISLR实测值与仿真值相比都有不同程度的损失，这是因为探测序列调制后通过短波电台时以及在传播过程中受到乘性干扰和加性干扰的影响，导致信号包络发生起伏变化，影响了相关运算的结果。

3.结 论

脉冲压缩体制短波信道斜向探测要求探测序列有优良的自相关特性。将Zadoff-Chu序列应用到短波信道探测中，设计了能充分利用其周期自相关特性的序列扩展方式，分析了序列的调制解调过程和相关检测，通过仿真和实测对Zadoff-Chu序列、m序列和巴克码的相关函数以及相关函数的PCM、MF、ISLR、PAPR值进行了分析比较。结果表明，与m序列和巴克码相比，Zadoff-Chu序列具有更优越的自相关特性；其相关函数的PCM、MF、ISLR和PAPR四个参数的值也比m序列和巴克码的相应参数的值更优越。所以，Zadoff-Chu序列在短波信道探测中有较高的应用价值。

［1］陈 曦，赵正予，时 雨，等.电离层斜向返回探测系统的主控制器研制［J］.电波科学学报，2005，20（5）:598-603.CHEN Xi，ZHAO Zhengyu，SHI Yu，et al.Design and implement of main-controller in ionospheric oblique backscattering sounding system ［J］.Chinese Journal of Radio Science，2005，20（5）:598-603.（in Chinese）

［2］王 烽，赵正予，李 婷.单站电离层探测系统自动跳频探测模式的设计与实现［J］.电波科学学报，2009，24（4）:604-609.WANG Feng，ZHAO Zhengyu，LI Ting.Design and implementation of auto hopped frequency sound mode in monostatic ionospheric sounding system［J］.Chinese Journal of Radio Science，2009，24（4）:604-609.（in Chinese）

［3］姚永刚，赵正予，谢树果，等 .电离层后向散射探测中m序列和FH序列的应用［J］.电波科学学报，2001，16（4）:522-528.YAO Yonggang，ZHAO Zhengyu，XIE Shuguo，et al.The applications of m sequence and FH sequence to ionospheric backscattering sounding［J］.Chinese Journal of Radio Science，2001，16（4）:522-528.（in Chinese）

［4］ZADOFF S，ABOUREZK W.Signal Identification and Alignment System:USA，3008125［P］.1961-11-07.

［5］HEIMILLER R C.Phase shift pulse codes with good periodic correlation properties［J］.IRE Transactions on Information Theory，1961，7（4）:254-257.

［6］FRANK R L，ZADOFF S.Phase shift pulse codes with good correlation properties［J］.IRE Transactions on Information Theory，1962，8（6）:381-382.

［7］CHU D C.Polyphase codes with good periodic correlation properties［J］.IEEE Transactions on Informa-tion Theory（Corresp.），1972，18（4）:531-532.

［8］KEBO A，KONSTANTINIDIS I，BENEDETTO J J，et al.Ambiguity and sidelobe behavior of CAZAC Coded Waveforms［C］／／IEEE Radar Conference，Boston，MA，USA.Boston:Raytheon Sudbury，2007:99-103.

［9］任 斌.CAZAC序列在LTE中的应用研究［D］.北京邮电大学，2009.REN Bin.Application Research of CAZAC Sequence in LTE［D］.Beijing University of Posts and Telecommunications，2009.（in Chinese）

［10］OGAWA Y，TAKATA T，IWAI T，et al.Pilot Signal generation scheme using frequency dependent cyclic shift sequence for inter-cell interference mitigation［C］／／IEEE Radio and Wireless Symposium，San Diego，CA.San Diego:IEEE Press，2009.

［11］EDMONSON P J，CAMPBELL C K，YUEN S F.Study of SAW Pulse Compression Using 5×5Barker Codes with Quadraphase IDT Geometries［C］／／Proceedings of IEEE Ultrasonics Symposium，Chicago，IL，USA.Chicago:IEEE ComSoc，1988.

［12］XIONG Fuqin.Digital Modulation Techniques［M］.Boston:Artech House，2000.

［13］郑应强，于素芬，张振仁.基于半带滤波器的 倍数字内插及其DSP的实现［J］.机电工程技术，2005，34（2）:35-37.ZHENG Yingqiang，YU Sufen，ZHANG Zhenren.Implement of digital interpolation by TMS320C5402 based on half-band filter［J］.Mechanical ＆ Electrical Engineering Technology，2005，34（2）:35-37.（in Chinese）

［14］JAMIL M，LINDE L P.A comparison of unfiltered and filtered complex spreading sequences based on aperiodic correlation properties［C］／／Proc.IEEE 5th International Symposium on Spread Spectrum Techniques and Applications，Sun City，South Africa.Sun City:IEEE ComSoc，1998.

［15］MIRZAEE A，AGHAEINIA H.Design of a new class of spreading sequence using chaotic dynamical systems for asynchronous DS-CDMA applications［C］／／Proc.IEEE Ninth International Symposium on Computers and Communications，Cairo，Egypt.Cairo:IEEE ComSoc，2004.

［16］EAVES J L，REEDY E K.Principles of Modern Radar［M］.New York:Van Nostrand Reinhold Company，1987.

［17］LIM D W，NOH H S，JEON H B，et al.Multi-stage TR scheme for PAPR reduction in OFDM signals［J］.IEEE Transactions on Broadcasting，2009，55（2）:300-304.