等几何分析法应用于偏心柱面静电场问题

张 勇 林 皋 刘 俊 徐喜荣

（1.大连理工大学建设工程学部，辽宁 大连 116024；2.大连理工大学电子信息与电气工程学部，辽宁 大连 116024）

引 言

由两根圆柱导体所组成的传输线在实际工程中有着极为广泛的应用，由于特殊要求或者制造的误差，常常呈现偏心状态，是柱面或是椭圆形式的，其静电场边值问题成为静电学中的典型问题。

计算电磁学是电磁学分析的一种重要工具，其中对静电场求解是最为基础和重要的环节。计算电磁学主要有解析法、半解析法和数值解法三大类。解析法虽然能够得到精确的解析式，清晰地看出各物理量间的依赖关系，但其只适用于简单的求解域、简单的物理参数，不具有通用性。半解析法有级数法、配置点法、多极理论方法和新型等效源法［1-4］等方法。这些方法在计算电磁学中取得了较好的效果和应用，但该类方法也只适用一些几何形状比较规则的静电场问题。数值解法有有限差分法、有限元法、边界元法、矩量法、无网格法［5-12］等。其中，有限元法是应用最为广泛的数值方法，是分析静电场问题最强大、最通用方法之一，适合于含有复杂媒质问题的数值分析。但该方法在处理含有场值奇异以及不同材料交接点等问题中遇到很大的挑战，通常的处理方法是在这些点周围处增加节点，但这势必需要更多的前处理和计算工作时间，当然也有很多改进的有限元方法，例如提高形函数或者使用超级单元等。各类数值方法都需要对求解域进行离散，而离散之后的计算模型可能与原模型不具有一致性，从而丧失精度。

等几何分析方法（IGA）是2005年由 Hughes［13］率先提出的一种新型数值方法。该方法剔除了传统数值方法的求解域的模型非一致性，从而实现了将问题的分析计算构架于精确模型上，实现较高的计算精度与效率。目前，这种方法已被用于求解固体力学和流体力学问题［14-19］。本文首次将该方法应用于静电场问题的求解。从静电场控制方程—拉普拉斯方程出发，结合加权余量法推导了静电场问题的等几何分析方程。

应用本文方法求解偏心圆柱面静电场问题，通过与传统方法和解析解的比较，等几何分析方法显示出低自由度消耗、高效性和精确性。

1.B样条和NURBS

1.1 B样条和NURBS基函数

B样条是由B样条基函数Ni，p（i=0，1，…，n），控制点Pi（i=0，1，…，n）和节点向量Ξ=｛ξ0，ξ1，…，ξm｝定义的。B样条基函数将节点向量所在的参数空间中的点映射到控制点所在的物理空间，从而B样条参数空间的一个参数区间［ξi，ξi+1）与物理空间中的一个单元Vi相对应。一维节点向量Ξ=｛ξ0，ξ1…，ξm｝是一组参数空间中的非递减的坐标序列，这里ξi是节点，i是节点标号。

一维空间B样条基函数Cox-de Boor公式［20］，递归定义为式（1），p为基函数的次数。

如果节点在参数空间中是等间距的则称为均匀B样条，否则，称为非均匀B样条。节点重数是指节点在节点向量中出现的次数，重数大于1的节点定义为多重节点。如果一个节点向量的第一个和最后一个节点是p+1重的，那么它是开放的。开放节点向量是计算机辅助设计（CAD）标准，本文也采用开放节点向量。B样条通常没有插值性，即控制点并不在B样条曲线上，即使开放节点向量的B样条也仅仅插值于端点。节点向量为｛0，0，0，1，2，3，4，4，4｝的基函数如图1所示。

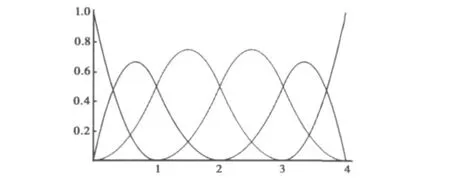
图1 二次NURBS基函数

非均匀有理B样条 （NURBS）是通过B样条有理化实现的，关系式为

式中:ωi是Ni，p（ξ）相应的权值，所以，NURBS具有与B样条一样的性质，如非负性、单位分解性、紧支性、灵活连续性和线性无关性等。与B样条相比，它可以更准确地建立圆锥曲线和曲面。若权值相等，则NURBS基函数退化为B样条基函数。

高维NURBS基函数可用低维NURBS基函数张量积得到，如式（3）所示的二维NURBS基函数形式，p、q分别为两个方向基函数的次数。

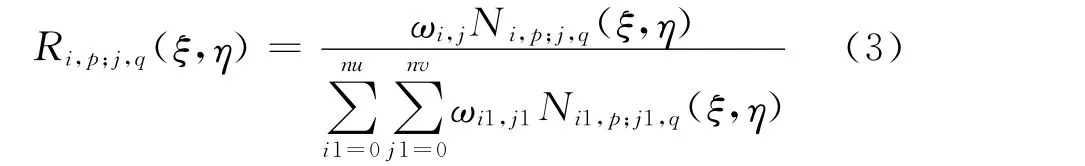
1.2 基于NURBS的几何形体表示方法

NURBS曲线用向量形式表示为

式中:Pi是NURBS曲线控制点。图2、图3给出了一典型的NURBS曲线，采用的基函数如图1所示。

对于NURBS曲面也有相似的形式，且为

2.基于NURBS的静电场等几何分析方法推导

2.1 静电场问题

静电场问题是电磁学分析中的一个典型边值问题（BVP），描述静电场（域内无电荷）特性的控制方程（φ为电势）为

2.2 求解域的等几何离散

求解域采用NURBS离散，节点向量表示为Ξ=｛ξ0，ξ1，…，ξku-1｝，Η=｛η0，η1，…，ηkv-1｝。参数域内的节点区间［ξh，ξh+1）×［ηk，ηk+1）映射成求解域上的一个单元Vh，k，相应的非零NURBS基函数索引为（h1，k1），其中，h1=p-h，p-h+1，…，p，k1=qk，q-k+1，…，q，p、q分别为两个方向基函数次数。根据NURBS基函数的紧支性，单元Vh，k的所有非零基函数个数为（p+1）（q+1），与该单元的控制点数量相同。求解域NURBS单元Vh，k的任一点坐标表示为

式中:X（ξ，η）h，k=｛X（ξ，η）h，k，Y（ξ，η）h，k）｝表示求解域中 NURBS单元Vh，k任一点坐标；=（，）表示相应与该单元的控制点坐标；xh，k表示该单元所有控制点坐标列向量；是等几何分析基函数，可表示B样条基函数或NURBS基函数的张量积形式；NBh，k（ξ，η）是相应的矩阵形式。

为简化，以后的符号中省掉单元上标h，k.图4给出了一典型被NURBS离散的求解域，控制点标记为·，黑色虚线表示控制网，绿色曲线表示NURBS单元的边界，控制点的非插值性如图4所示。

图4 NURBS离散求解域

2.3 求解域的保形细化

求解域的保形细分是等几何分析的重要特征，对于初始的模型，可以通过保形细分得到与原模型相一致的细化模型。保形细分算法有h-细化方法，p-细化方法，k-细化方法等［13］。

2.4 电势场的等参化

等参方法用于近似求解域的电势场，求解域中的任一点的电势具有与式（7）相似的表示形式。

式中:φi表示求解域控制点的电势场变量。

2.5 等几何分析方法离散方程

控制微分方程式（6a）是采用Galerkin加权余量法或者虚功原理［21］求得的。推导过程从略，等几何分析方法离散方程可表示为

关于控制点电势的方程，K=表 示NURBS单元系数矩阵集成的总体系数矩阵为

公式（10）的积分区间是 NURBS单元Vh，k的参数区间［ξh，ξh+1）×［ηk，ηk+1），不是非标准的高斯积分区间，计算积分时需要转化，对于不同的单元这个积分区间是不同的。

Q=是等效控制点激励，包括体电荷分布和第二类边界条件的贡献，表达式为

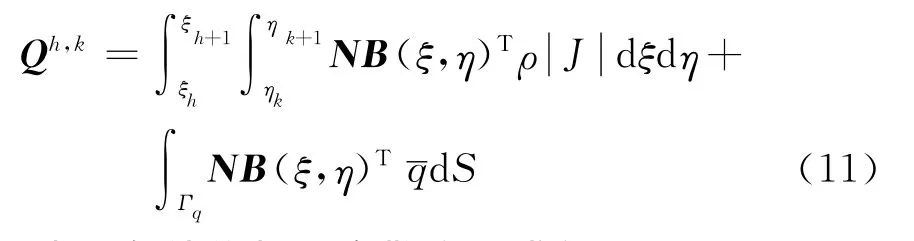
2.6 边界条件施加及离散方程求解

NURBS单元的控制点不具有插值性，边界条件的施加相对与传统的有限元有较大的区别。对于第一类边界条件，利用NURBS基函数的非负性将与边界相关的单元的控制点分成两组，在Γφ上恒为零的和不恒为零的。

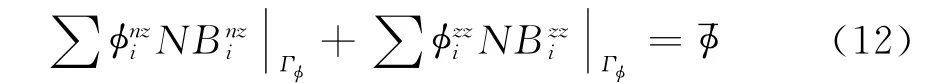
恒为零的基函数对应的控制点对电势没有贡献，即式（12）只剩下非负基函数对应的项，再利用NURBS基函数的单位分解性，可得

从而将求解域上的边界约束条件转化到控制点上。

第二类边界条件贡献，即式（11）的第二项，利用边界积分，将边界微元转化到参数域中进行。

对于不同的边界面，边界微元形式和积分区间也不尽相同，例如，对于U参数ξh边界面，形如式（15）.

3.偏心柱面静电场问题算例分析

3.1 偏心圆柱面

偏心圆柱面静电场问题［22］，即一圆柱面（半径为R2，轴线为L2）位于另一个圆柱面（半径为R1，轴线为L1）的内部，两圆柱面上的电势分别为V2和V1，但两圆柱面的轴线L1与L2不重合，且轴线间距为L，求解两圆柱面夹层之间的电势分布问题。

上述问题简化为平面问题，如图5所示，其电势解析解为

式中:C0、A0、x1、x2为计算系数，与偏心圆柱面的几何尺寸R1、R2、L及电场参数V2和V1有关。

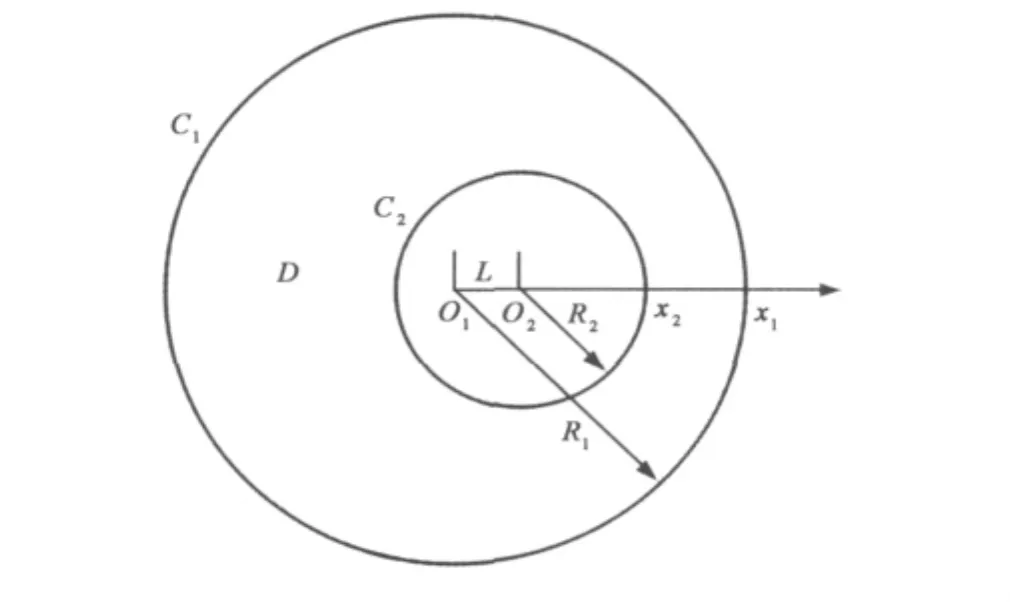
图5 偏心圆柱面示意图

在仿真中，取R1=1.0m，R2=0.5m，L=0.2m，V1=0V，V2=1V.利用求解域与边界条件的对称性，只取上半部分进行分析，如图6所示。

图6 偏心圆柱面计算简图

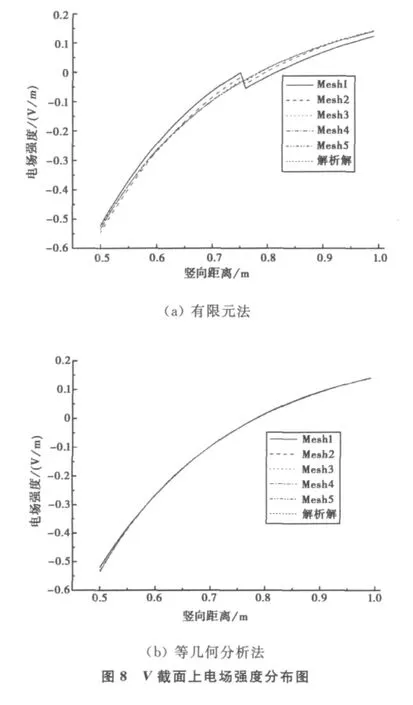
为了比较解的收敛性和收敛速度，采用五种尺寸的单元划分，对于每一种尺寸的网格，分别对应一个等几何单元模型和一个传统的有限元单元模型，计算自由度数量和单元数量在表1中列出，并在图7中显示。随着单元数量的增加，传统有限元单元模型的计算自由度迅速增加，而等几何单元模型的计算自由度增加的速率明显缓慢，这源于等几何分析单元之间可以共享更多的自由度。在图6所示的典型截面上电场强度的分布如图8所示。图8（a）为有限元计算的结果，在单元过度处出现震荡，即使很细的网格也未能幸免，而图8（b）所示的等几何分析计算结果，和解析解的误差甚小，且不出现震荡。

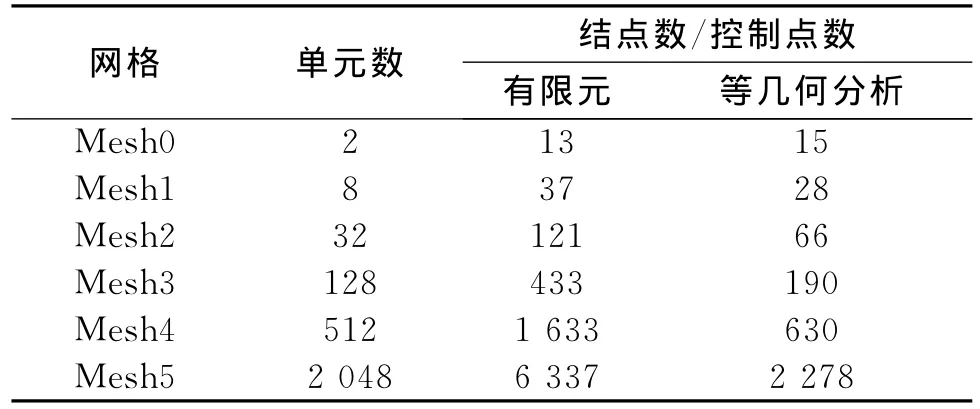
表1 各种网格下的单元数量和自由度数量

图7 计算自由度与单元数量图

整个求解域的相对解析解的误差计算公式为式（17），φi-exact为解析解，φi-calc为数值解。

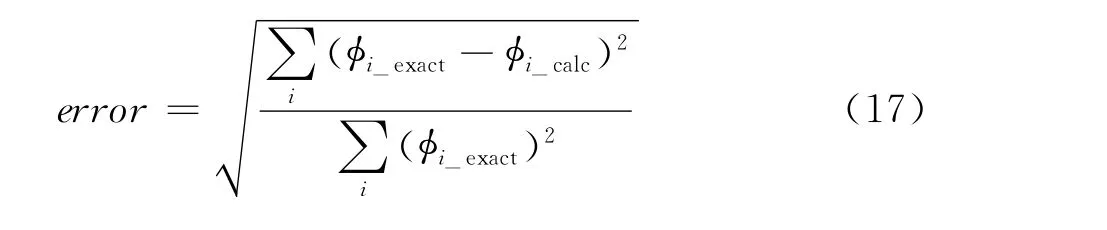
电势的相对误差随网格尺寸变化如图9所示，随着单元尺寸的减少，传统有限元Lagrange单元和NRUBS等几何单元的计算结果的相对误差都减少，而在每个网格尺寸下后者比前者小得多，可见其精度高，收敛速度快。

图9 电势的相对误差随网格尺寸变化图

整个域上的电势（单位:V）分布图如图10（见212页）所示，图10（a）与（b）分别是IGA的数值解及其和解析解的相对误差分布图，误差很小，只有10-7数量级，可见其求解精度高。

从偏心圆柱面静电场问题可以看出，一方面等几何分析方法天然地具有等几何性，即计算模型与设计模型一致，且还拥有细化保形性；另一方面等几何分析方法在计算方面还具有单位单元的计算自由度消耗小，计算精度高，收敛速度快的特点。

3.2 偏心椭圆柱面

偏心椭圆柱面与偏心圆柱面类似，只是带电体是椭圆柱面，如图11所示。

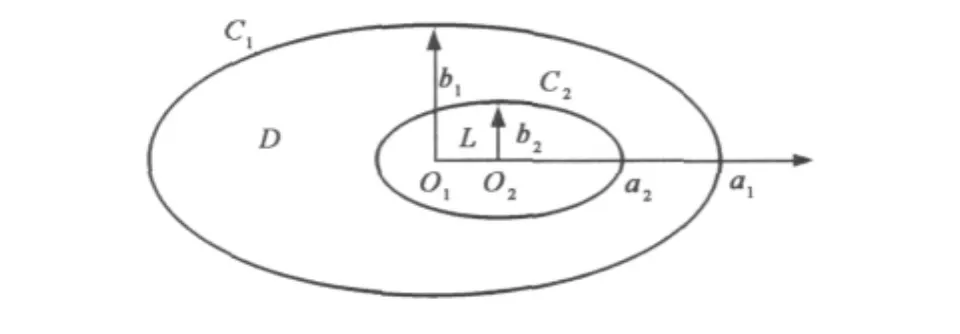
图11 偏心椭圆柱面计算简图

在仿真中，取长半轴a1=1.0m，a2=0.5m，b1／a1=b2／a2=0.5，L=0.2m，V1=0V，V2=1V.

柱面形状的改变使得解析法很难进行。在3.1节中的收敛性分析的基础上，直接给出了等几何分析的求解结果分布图，如图12（见212页）所示。从图中可以看出，电势在偏心方向比较集中，且此处的电场强度较高。

4.结 论

将等几何分析方法扩展到静电场问题，推导了静电场问题的等几何分析方法求解格式。该方法具有细化保形性，计算自由度少，收敛速度快，计算精度和计算效率高的特点。并应用此方法求解了偏心圆柱面和偏心椭圆柱面的静电场问题，结果表明了该方法具有上述的优点，适合进一步在计算电磁学中推广。

［1］李 敬.级数法求解轴对称的静电场［J］.云南师范大学学报，1997，17（3）:43-45.LI Jing.Inprogression resolution statics field with symmetric axis［J］.Journal of Yunnan Normal University:Natural Sciences Edition，1997，17（3）:43-45.（in Chinese）

［2］马西奎.最小二乘边界配点法在电磁场边值问题数值分析中的应用［J］.微波学报，1994，37（2）:17-22.MA Xikui.Application of least square boundary point matching method to the numerical analysis of electromagnetic field problems［J］.Journal of Microwares，1994，37（2）:17-22.（in Chinese）

［3］BALLISTI R，HAFNER C.The multiple multipole method in electro-and magnetostatic problems［J］.IEEE Transactions on Magnetics，1983，19（6）:2367-2370.

［4］盛剑霓.电磁场与波分析中半解析法的理论方法与应用［M］.北京:科学出版社，2006:1-35.

［5］周 勤，茅乃丰.旋转对称静电场的一种新的数值解法［J］.电波科学学报，1990，5（4）:26-34.ZHOU Qin，MAO Naifeng.The electrostatic field problems with representations of spline functions and their quasi-charge density analysis method［J］.Chinese Journal of Radio Science，1990，5（4）:26-34.（in Chinese）

［6］SONG B，FU J.Modified indirect boundary element technique and its application to electromagnetic potential problems［J］.IEE proceeding-h of Microwaves Antennas and Propagation，1992，139（3）:292-296.

［7］金建铭.电磁场有限元方法［M］.西安:西安电子科技大学出版社，1998:51-70.

［8］BAMJI S S，BULINSKI A T.Electric field calculations with the boundary element method ［J］.IEEE Transactions on Electrical Insulation，1993，28（3）:420-424.

［9］甄蜀春，曹 蕾，张继龙.波动方程差分解法对波导螺钉调配器的分析［J］.电波科学学报，2005，20（1）:125-127.ZHEN Shuchun，CAO Lei，ZHANG Jilong.Analysis of screw tuner based on wave equation finite difference method［J］.Chinese Journal of Radio Science，2005，20（1）:125-127.（in Chinese）

［10］汪朝晖，廖振方，陈德淑.有限元法分析尖板电极结构的空间静电场分布［J］.重庆大学学报，2010，33（5）:41-47.WANG Zhaohui，LIAO Zhenfang，CHEN Deshu.A-nalysis of spatial electric field with point-plate electrodes configuration using finite element method［J］.Journal of Chongqing University，2010，33（5）:41-47.（in Chinese）

［11］梁志伟，赵国伟，徐 杰，等.柱形等离子体天线辐射特性的矩量法分析［J］.电波科学学报，2008，23（4）:749-753 LIANG Zhiwei，ZHAO Guowei，XU Jie，et al.A-nalysis of plasma-column antenna using moment method［J］.Chinese Journal of Radio Science，2008，23（4）:749-753.（in Chinese）

［12］张淮清.电磁场计算中的径向基函数无网格法研究［D］.重庆:重庆大学，2008.ZHANG Huaiqing.Research on Radial Basis Function Meshless Method in Numercial Computation of Electromagentic Field［D］.Chongqing:Chongqing U-niversity，2008.（in Chinese）

［13］HUGHES T J R，COTTRELL J A，BAZILEVS Y.Isogeometric analysis CAD， finite elements，NURBS，exact geometry and mesh refinement［J］.Comput.Methods Appl.Mech.Engrg.，2005，194（39／40／41）:4135-4195.

［14］REALI A.An isogeometric analysis approach for the study of structural vibrations［J］.Journal of Earthquake Engineering，2006，10（Special Issue 1）:1-30.

［15］BAZILEVS Y，CALO V M，ZHANG Y，et al.Isogeometric fluid-structure interaction analysis with applications to arterial blood flow［J］.Computational Mechanics，2006，38（4／5）:310-322.

［16］COTTRELL J A，REALI A，BAZILEVS Y，et al.Isogeometric analysis of structural vibrations［J］.Computer Methods in Applied Mechanics and Engineering，2006，195（41／42／43）:5257-5296.

［17］COTTRELL J A，HUGHES T J R，REALI A.Studies of refinement and continuity in isogeometric structural analysis［J］.Computer Methods in Applied Mechanics and Engineering，2007，196（41／42／43／44）:4160-4183.

［18］ZHANG Y，BAZILEVS Y，GOSWAMI S，et al.Patient-specific vascular NURBS modeling for isogeometric analysis of blood flow［J］.Computer Methods in Applied Mechanics and Engineering，2007，196（31／32）:2943-2959.

［19］ZHANG Y，LIN G，HU Z Q.Isogeometric analysis based on scaled boundary finite element method［J］.IOP Conference Series:Materials Science and Engineering，2010，10（1）:012237.

［20］PIEGL L，TILLER W.The NURBS Book［M］.Berlin:Springer Verlag，1997.

［21］HUGHES T J R.The Finite Element Method，Linear Static and Dynamic Finite Element Analysis［M］.New York:Dover，2000.

［22］陈云林，李 旭，兰明建.偏心圆柱面静电场电势分布和电场强度分布的求解［J］.渝西学院学报，2002，1（4）:28-31.CHEN Yunlin，LI Xu，LAN Mingjian.The solution for the electrical potential and electrical field intensity s distribution inside two parallel conductor cylinders whose axes are separated［J］.Journal of Western Chongqing University，2002，1（4）:28-31.（in Chinese）