基于GSVSC理论的STT导弹控制系统设计

董飞垚 ，雷虎民 ，陈伟伟，李 炯

（1.空军工程大学导弹学院，陕西 三原 713800；2.西安工业大学，陕西 西安 710032）

0 引言

随着载体机动性的日益增强及作战环境的变化，对导弹的战术技术指标要求不断提高，导弹制导控制系统的复杂性和战术技术指标间的矛盾越来越突出，传统设计已不能满足未来战争对导弹战术技术指标的要求［1］。近年来，自适应控制、非线性控制和增益调度等方法被用于导弹控制系统设计。增益调度控制概念简单且实际证明有效，但事实上无法保证控制的稳定性。当飞行器的非线性增强时，根据飞行包线的离散点设计的控制器增益需作不断调整以获得最佳性能，否则当系统非线性显著增强或建模误差较大时，控制系统性能将急剧变差。作为一种非线性控制方法，滑模变结构控制对模型不确定性和外部干扰有很强的鲁棒性，具有结构简单、设计步骤清晰、性能评价函数形式易懂、控制过程不受系统外界干扰和参数摄动的影响等特点，在飞行器控制中获得广泛应用。滑模控制系统设计一般分为两步：在状态空间中选择滑模面，当系统状态到达该滑模面后，由滑模面方程限制系统的动态，使系统对外部干扰和不确定性有较强鲁棒性；其后设计系统的控制输入，使滑模面外的系统状态在有限时间内到达滑模面，并让状态运动保持在该滑模面上［2－6］。

传统滑模控制存在能达阶段的鲁棒性和抖振等不足。模型跟踪全局滑模变结构控制作为一种新型滑模变结构控制方案，通过引入全程滑态因子，使系统在开始阶段就处于滑模面上，克服了传统滑模变结构控制不具鲁棒性的问题，在控制项中采用饱和函数代替符号函数，有效解决了抖振［7－10］。本文对模型跟踪全局滑模变结构控制进行了研究。

1 导弹纵向通道的数学模型

在小扰动假设条件下，导弹纵向通道短周期运动数学模型可表示为

式中：Ap＝；Bp＝［Bp1Bp2］Τ；Xp＝；ny为导弹的纵向过载；up＝δz为舵偏角；ΔAp，ΔBp为参数摄动，且‖ΔAp‖≤ψa，‖ΔBp‖≤ψb；f为外界干扰，且‖f‖≤ψf。此处：Ap11＝0；Ap12＝1；Ap21＝a1a4－a2；－a1＋a4；Bp1＝0；Bp2＝（a2a5－a3a4）vm／（57.3g）；ψa，ψb，ψf均为大于零的常数；a1，a′1，a2，a3，a4，a5为时变且摄动的导弹气动参数；vm为导弹速度；g为重力加速度。

由式（1）可知：导弹是参数时变且变化范围很大的被控对象，欲提高其命中精度，需用先进控制理论进行控制系统设计。

2 模型跟踪GSVSC控制算法

模型跟踪GSVSC控制综合了跟踪控制和滑模变结构控制，取参考模型与实际系统输出的误差及其微分量为相应的状态变量，进行滑模面和控制算法的设计。模型跟踪全局滑模变控制系统结构如图1所示。

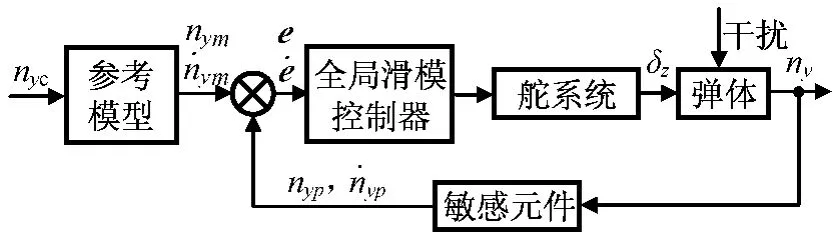
图1 模型跟踪全局滑模变控制系统结构Fig.1 Structure of model tracking GSVSC

2.1 误差模型描述及模型完全跟踪条件

由式（1），取参考模型

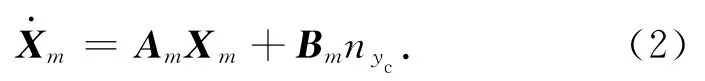
式中：Am＝；Xm＝；Am11＝0；Am12＝1；Am21＝－1／（Tm）2；Am22＝－2ξm／Tm；Bm＝［01］Τ；为过载指令。此处：Tm，ξm分别为时间常数和阻尼比，由控制系统的设计指标确定。

定义误差系统的状态向量

由参考模型式（2）和被控对象式（1）可得模型跟踪系统的误差模型为

式中：δz为导弹俯仰舵偏角。

若欲实现被控对象对参考模型的完全跟踪，则应成立

对式（4），控制量up应满足

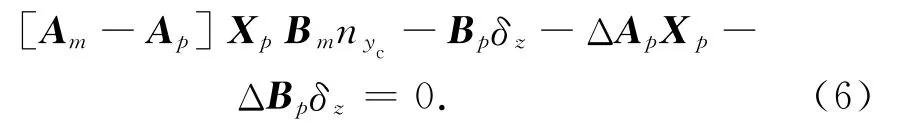
根据线性代数理论可得被控对象对参考模型完全跟踪的充分条件为

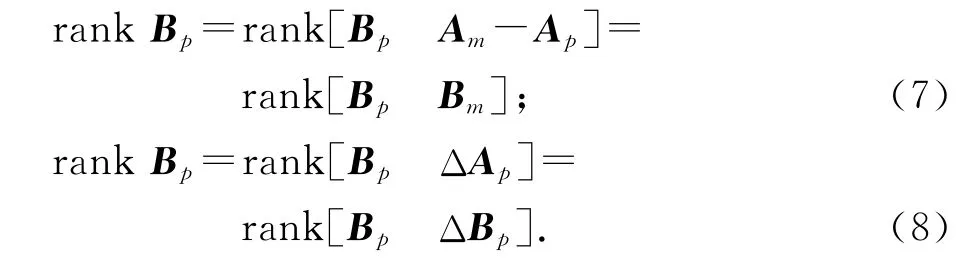
结合模型参数可得，式（1）所描述系统满足式（7）、（8），即满足对参考模型完全跟踪的充分条件，故可进行模型跟踪全局滑模变结构控制算法设计。

2.2 控制算法设计

变结构控制律可表示为

式中：uv为变结构控制律；um为匹配控制律，且

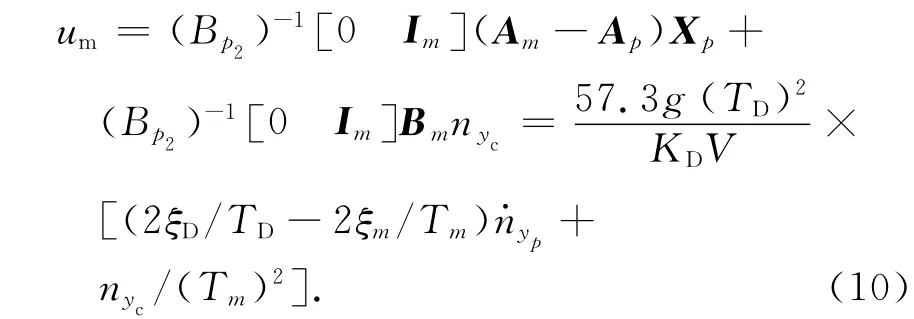
此处：Im为m阶单位阵；KD，TD，ξD分别为弹体传递系数、时间常数和阻尼比。

根据系统设计指标，利用极点配置法得到系统期望极点集为｛p｝，则滑态移动参数

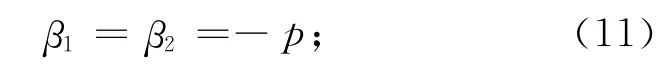
滑态参数阵为

则全程滑态因子

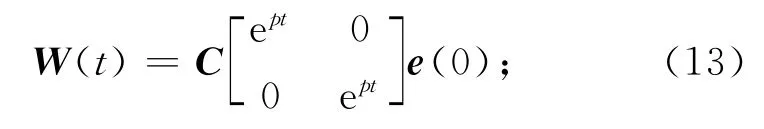
滑动超平面

将式（9）、（10）代入式（4），可得

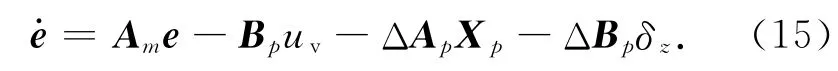
针对式（15），为保证系统可靠地保持在滑模面s上，取

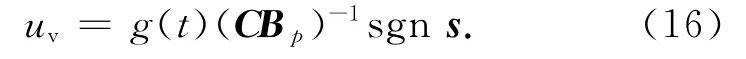
式中：g（t）为待求的标量控制系数，且g（t）＞0。

2.3 稳定性分析

选 取Lyapunov函 数 为V（s）＝，则＝sTs。将式（16）代入；可得

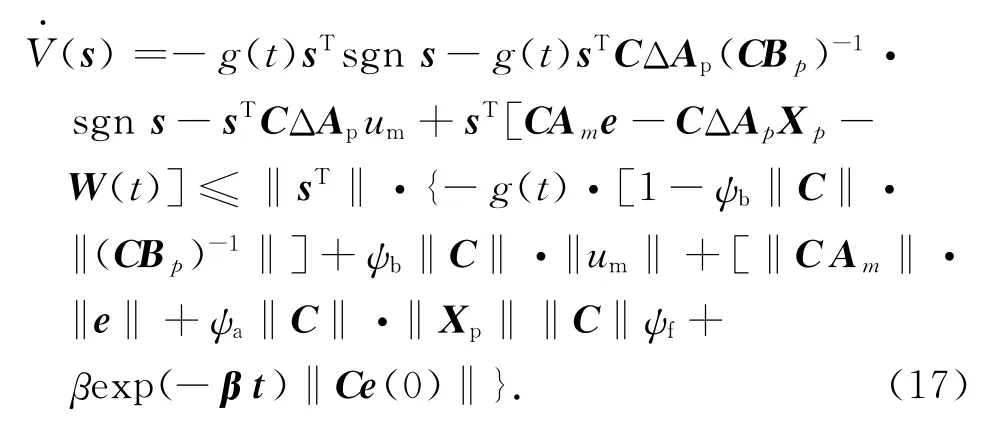
取控制系数

为消除高频抖动，采用饱和函数代替符号函数，可将不连续控制转化为连续控制，削弱抖振，饱和函数可表示为

式中：δ为小正数。则式（16）转化为

式（9）～（16）即为基于模型跟踪全局滑模变结构控制理论设计的控制算法。

3 仿真

针对导弹控制系统进行全空域数字仿真。仿真中，取导弹气动参数摄动范围为±20%，考虑实际舵机转角、转速的限制，饱和函数小正数项δ＝0.005，Tm＝0.7s，ξm＝0.8，仿真结果如图2～7所示。

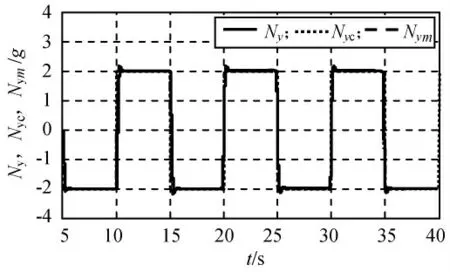
图2 方波过载指令跟踪结果Fig.2 Tracking of over－load under square wave order

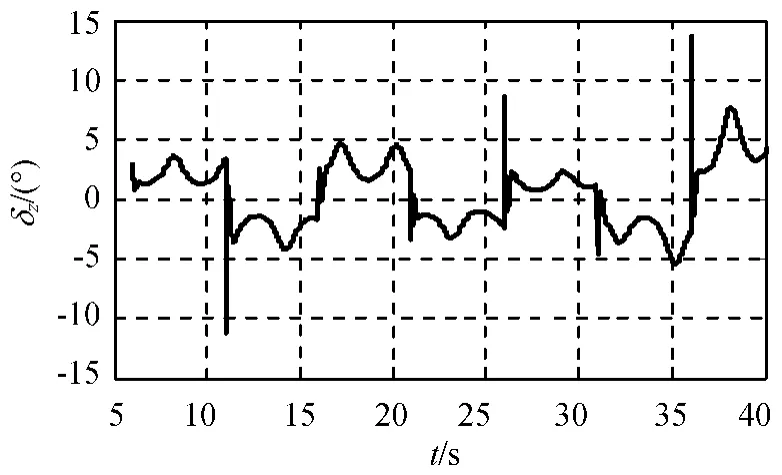
图3 方波过载指令跟踪时的δzFig.3 δzunder square wave order

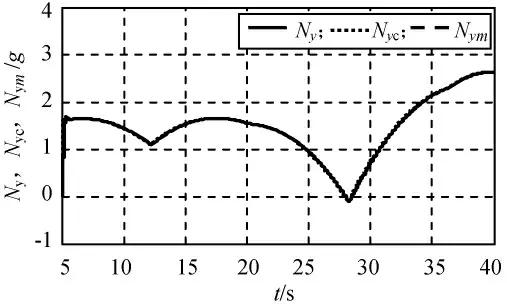
图4 典型弹道过载指令跟踪结果Fig.4 Tracking of overload under typical ballistic order

由图2～7可知：在模型参数摄动状态下，控制系统在低空、中空和高空均有良好的动态性能和模型跟踪性能。动态性能指标为：80%的上升时间不大于0.2s，超调量小于10%，满足导弹控制系统的设计指标要求。同时由于在设计滑模面中引入全程滑态因子，使系统在开始阶段就能保持在滑模面上，克服了传统滑模控制鲁棒性和抗干扰能力差的特点。

图5 跟踪典型弹道过载指令时的δzFig.5 δzunder typical ballistic order

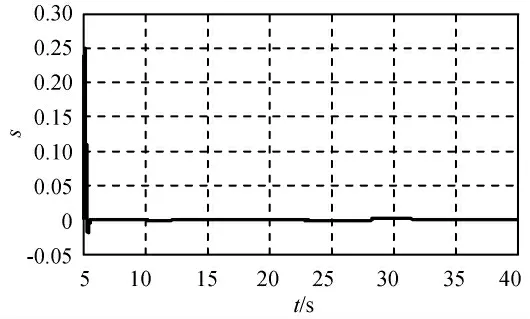
图6 跟踪典型弹道过载指令时滑模面sFig.6 s under typical ballistic order

图7 跟踪典型弹道过载指令时的e，Fig.7 e，under typical ballistic order

4 结束语

本文提出一种导弹纵向通道的数学模型，并对模型跟踪GSVSC控制算法进行了研究，通过误差模型描述对控制算法进行设计，分析其稳定性。仿真结果表明：基于模型跟踪全局滑模控制理论设计的导弹控制系统能准确快速地跟踪制导指令信号，克服了传统设计方法的不足，更能适应未来的战场环境。

［1］刘智平，周凤岐，周 军.战术导弹现代自动驾驶仪设计方法综述［J］.航天控制，2006，24（5）：91－96.

［2］JALILI－KHARAAJOO M，EBRAHIMIRAD H.Improvement of second order sliding－mode controller applied to position control of induction motors using fuzzy logic［R］.IFSA，2003：508－515.

［3］EDWARDS C.A practical method for the design of sliding mode controllers using linear matrix inequalities［J］.Automatica，2004，40（10）：1761－1769.

［4］ERTUGRUL M，KAYNAK O.Neuro sliding mode control of robotic manipulators［J］.Mechatronies，2000，10（1）：239－263.

［5］BHAT M S，BAI D S，POWLY A A.Variable structure controller design with application to missile tracking［J］.Guidance，2000，24（4）：859－862.

［6］HU Q L，MA G F，SHI Z.Integral variable structure／input shaping control of flexible spacecraft［J］.IEEE Transactions on Automatic Control，2003，48（2）：929－934.

［7］陈 洁，顾文锦，周绍磊.基于二阶滑模的导弹控制系统设计［J］.北京航空航天大学学报，2009，35（3）：322－325.

［8］XIAO L F，SU H Y，ZHANG X Y，etal.Discrete variable structure control algorithm for nonlinear systems via sliding mode prediction［C］／／Proceedings of the 2006American Control Conference.Minneapolis，Minnesota：［c.n.］，2006：4712－4717.

［9］吴振辉，董朝阳.直接力／气动力复合控制导弹自适应模糊滑模控制［J］.北京航空航天大学学报，2007，33（9）：1051－1055.

［10］MOON G，KIM Y.Variable structure control with optimized sliding surface for aircraft control system［C］／／AIAA Guidance，Navigation，and Control Conference and Exhibit.Rhode Island：AAAA，2004：1－9.