CAT(0)空间中平均非扩张映射不动点的存在性定理及其半闭原理*

崔云安，周 晶

(哈尔滨理工大学)

1 预备知识

定义1.1 设C是度量空间(M，d)的一个非空子集.映射T:C→C被称为非扩张的是指:对所有x，y∈C，

定义1.2 设C是度量空间(M，d)的一个非空子集.称映射T:C→C是平均非扩张的，是指:对任意a，b≥0，a+b≤ 1，

成立，其中x，y∈C.

很明显，非扩张映射是平均非扩张映射的一种，但是平均非扩张映射不一定是非扩张的，因为平均非扩张并不能保证映射的连续性.

例 假设映射T:［0，1］→［0，1］有如下定义

那么T是满足的平均非扩张映射.但是T在处不连续，因此T并不是非扩张映射.

在众多的关于非扩张映射的研究中，其中一个十分重要的且值得庆祝的结果就是1968年由Browder提出的半闭原理［1］.

定义1.3 如果X是一致凸Banach空间，C是X的一个非空子集，T:C→X是非扩张映射，那么对每个y∈X，称Ⅰ-T是半闭的，是指:若{xn}⊂C满足及(Ⅰ-T)xn→y，则(Ⅰ-T)x=y，此处Ⅰ是X到其自身的恒同算子.

2008 年，Suzuki［2］引入了 Banach 空间中的Suzuki广义非扩张映射.

定义1.4 设C为(M，d)的一个非空子集.称映射T:C→C是Suzuki广义非扩张的，是指:对于所有x，y∈C，如果，那么则有

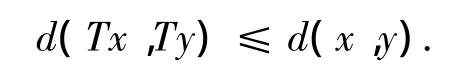
2 主要定理

定义2.1 设Δ是M中的测地三角形，为Δ的比较三角形.称测地空间M为CAT(0)空间，是指:M中任意的测地三角形都满足CAT(0)不等式，即对∀x，y∈Δ，以及比较点∈，都有

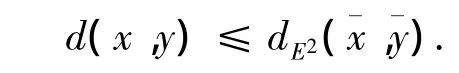
CAT(0)空间是凸的度量空间，是指:对∀x，y∈M及t∈［0，1］，存在唯一的一点z∈［x，y］，满足d(x，z)=td(x，y)，d(y，z)=(1-t)d(x，y).为方便起见，记上式中的z为(1-t)x⊕ty.如果M为CAT(0)空间，则对任意的x，y，z∈M，及t∈［0，1］，都有

同时，CAT(0)不等式蕴含着

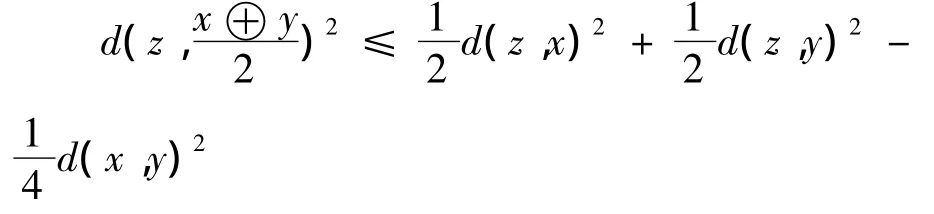
这就是由 Bruhat和 Tits［3］提出的著名的(CN)不等式.事实上，测地空间M为CAT(0)空间的充要条件是M满足(CN)不等式.2005年至2010年，关于CAT(0)空间中的单值和集值映射的不动点问题的新结果不断涌现［4-8］.

定理2.2 设(M，d)是一个完备的CAT(0)空间，C是M的一个非空有界闭凸子集.则满足b＜1的平均非扩张映射T:C→C有不动点.

证明 对任意y∈C，考虑

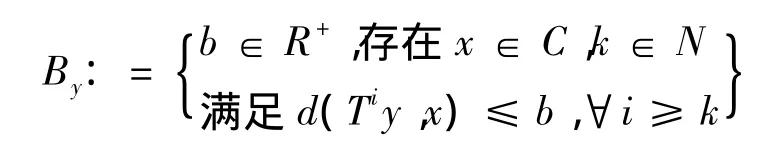
易知，diam(C)∈By，因此By非空.令βy:=infBy，则对任意θ＞0，存在bθ∈By满足

bθ＜βy+θ，从而存在x∈K以及k∈ℕ 满足

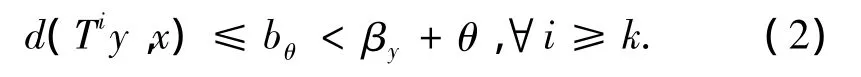
显然，βy≥0.下面分两种情况进行讨论:

情况1βy=0.

令ε＞0.在式(2)中取θ=ε/2，则存在x∈C及k∈ℕ，满足对∀m，n≥k，d(Tn，Tmy)≤

因此，序列{Tny}是基本列，利用C的完备性知，序列{Tny}收敛于某个元z∈C.显然，z是一个不动点.

情况2βy＞0.

对任意n≥1，定义在式(2)中取，那么存在

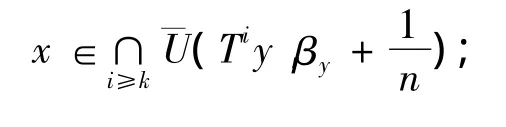
x∈C及k≥1，满足因此Dn非空.进一步，{Dn}是M中非增的非空有界闭凸集.因为CAT(0)空间具有非空交性质，所以.对任意的x∈D，易知

接下来，将证明对任意x∈D，{Tnx}是一个基本列.否则，存在ε0＞0及N0∈ℕ，使得

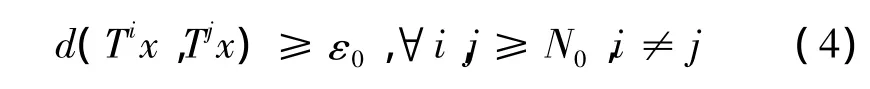
对上述ε0，取θ＞0使得

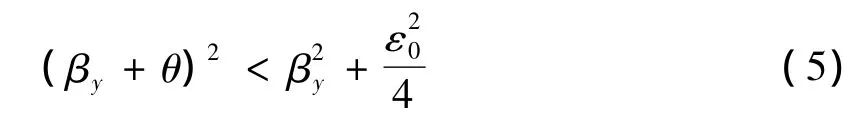
利用式(3)，存在K∈ℕ，使得

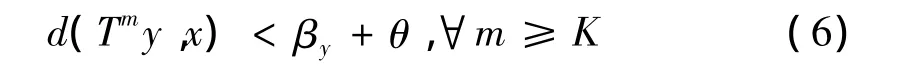
对任意给定的i，j≥N0，i≠j，结合式(6)以及T是平均非扩张的，对m＞i+K，

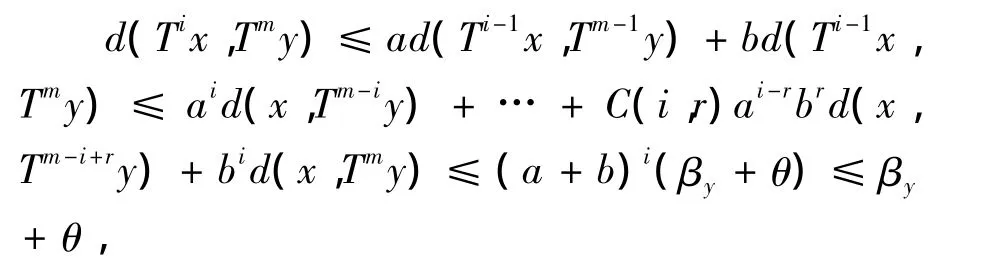
其中，C(i，r)表示从i中取出r个元素的组合数.同理可知，对任意m＞j+K，有d(Tjx，Tmy)≤βy+θ.因此，结合(CN)不等式以及(4)式和(5)式，有

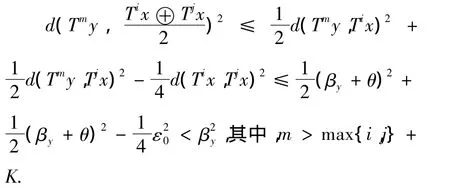
令z:，从而上述不等式对所有足够大的m均成立.由βy的定义βy=infBy，产生矛盾.

因此，对任意元x∈D，{Tnx}是一个基本列.利用M的完备性知，存在v∈C使得.最后，再次利用平均非扩张映射的定义，得到

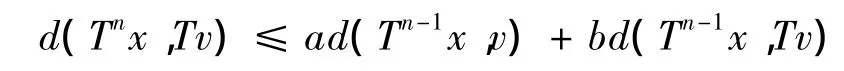
对上式两边同时取极限，有d(v，Tv)≤

bd(v，Tv).因为b＜1，从而有v=Tv，即v是T的一个不动点.

接下来证明CAT(0)空间中平均非扩张映射的半闭原理，在证明前首先需要定义以下符号:

其中，C是包含有界序列{xn}的闭凸集且

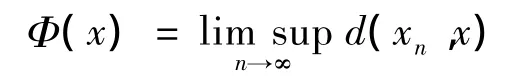
定理2.3 设(M，d)是一个完备的CAT(0)空间，C是M的一个非空有界闭凸子集.映射T:C→C是满足b＜1的平均非扩张映射.{xn}是C中的一列渐近不动点序列，即0并且那么T(w)=w.

证明 因为{xn}是一列渐近不动点序列，所以对∀m＞1，

从而，对∀x∈C，有Φ(Tmx)≤Φ(x)成立.采用数学归纳法.事实上，当m=1时，根据平均非扩张映射的定义以及(6)式，可得Φ(Tx)=

因此，Φ(Tx).可知，a+b≤1蕴含着Φ(Tx)≤Φ(x).假设，对任意的正整数k＜m，Φ(Tnx)≤Φ(x)均成立.那么

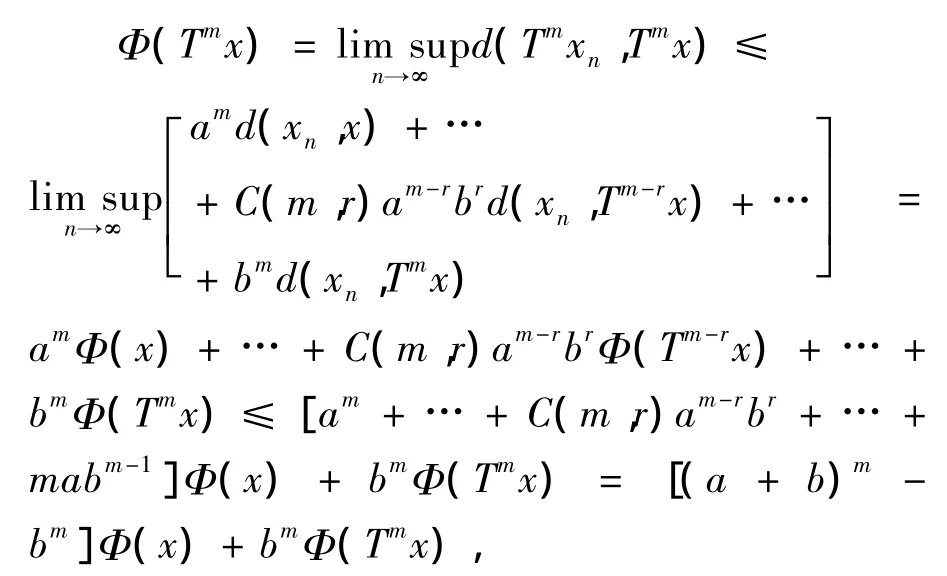
其中，C(m，r)表示从m中取出r个元素的组合数.因此，a+b≤1蕴含着Φ(Tmx)≤Φ(x).特别地，有

如果{Tmw}不含有按模收敛的子列，故能找到ε0＞0，使得

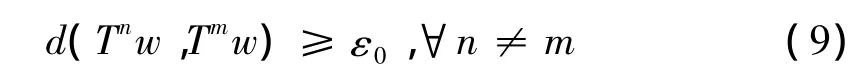
对上述ε0＞0，取θ＞0有

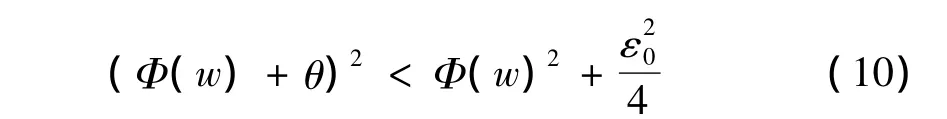
由Φ的定义及(8)式知，存在N，M∈ℕ，使得对∀m≥M，∀n≥N都有

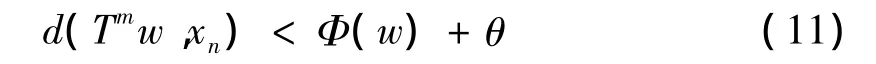
因此，结合(CN)不等式，(9)及(10)式，对任意的m1，m2≥M，可得

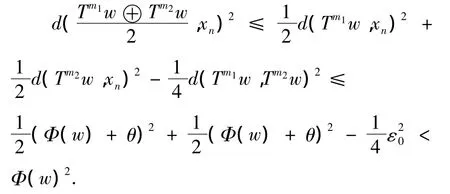
令z，那么z∈C并且z≠w.但是，产生矛盾.从而{Tmw}包含按模收敛子列，记为设那么

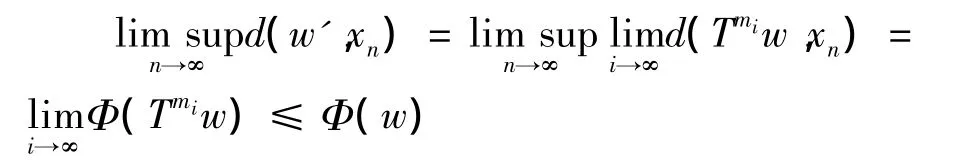
对上式两边同时取极限，有d(w，Tw)≤bd(w，Tw).因为b＜1，可得w=Tw.所以w是T的一个不动点，即

［1］ Browder F E.Semicontractive and semiaccretive nonlinear mappings in Banach spaces.Bull Am Math Soc，1968，74:660-665.

［2］ Suzuki T.Fixed point theorems and convergence theorems for some generalized nonexpansive mappings.J Math Anal Appl，2008，340:1088-1095.

［3］ Bruhat F，Tits J.Groupes R＇eductifs Sur un Corps Local.I.Donn＇ees Radicielles Valu＇ees［J］.1972，41:5 – 251.

［4］ Bridson M，Haeiger A.Metric spaces of non-positive curvature. Grundlehren derMathematischen Wissenschaften.Springer，Berlin，1999.319.

［5］ Dhompongsa S，Kaewkhao A，Panyanak B.Lim’s Theorems for Multivalued Mappings in CAT(0)Spaces［J］.J Math A-nal Appl，2005，312(2):478–487.

［6］ Dhompongsa S，Kirk W A，Sims B.Fixed Points of Uniformly Lipschitzian Mappings［J］.Nonlinear Anal，2006，65(4):762–772.

［7］ Dhompongsa S，Kirk W A，Panyanak B.Nonexpansive Setvalued Mappings in Metric and Banach Spaces［J］.J Nonlinear Convex Anal，2007，8(1):35–45.

［8］ Nanjaras B，Panyanak B.Demiclosed Principle for Asymptotically Nonexpansive Mappings in CAT(0)Spaces［J］.Fixed Point Theory Appl，2010，Article ID 268780:14.