脉冲管制冷机中板弹簧的有限元分析

李建国 闫 涛 蔡京辉

(1中国科学院理化技术研究所空间功热转换技术重点实验室 北京 100190)

(2中国科学院研究生院 北京 100190)

脉冲管制冷机中板弹簧的有限元分析

李建国1，2闫 涛1蔡京辉1

(1中国科学院理化技术研究所空间功热转换技术重点实验室 北京 100190)

(2中国科学院研究生院 北京 100190)

利用ANSYS有限元分析软件对外径为120 mm的板弹簧进行了应力和轴向刚度分析，得出了弹簧的厚度、涡旋角、涡旋槽个数以及涡旋槽宽度这些几何参数与其应力分布特性和轴向刚度性能的关系。首次提出了一个刚度应力比的概念，用刚度应力比值的大小来评价板弹簧性能的好坏，并将其作为板弹簧的设计依据。

脉冲管制冷机 板弹簧 有限元分析

1 引言

现代热成像技术、红外探测、跟踪、搜索系统的发展，对机械制冷技术提出了越来越高的要求，最典型的要求是工作寿命长、可靠性更高、制冷量更大［1］。脉冲管制冷机以其低温部分无机械运动部件、机械振动和电磁干扰小、寿命长的优点，成为一种理想的长寿命高可靠制冷装置。

现代脉冲管制冷机几乎均采用了间隙密封形式的线性压缩机技术，柔性板弹簧用于支撑制冷机压缩机活塞与膨胀活塞，保持运动过程活塞与气缸的密封间隙，为活塞往复振动提供足够刚度并且要有一定的行程［2］。因此，柔性板弹簧对于减少脉冲管制冷机中间隙密封的磨损、提高整体可靠性和工作寿命有着至关重要的作用。板弹簧的性能主要包括抗疲劳性和刚度性能。因此本文利用有限元分析方法对外径尺寸为120 mm的板弹簧进行了应力计算和轴向刚度计算，并首次提出了一个刚度应力比的概念，用刚度应力比值的大小作为评价板弹簧性能好坏的依据，为压缩机板弹簧的设计提供了重要的参考。

2 有限元分析方法及过程

有限元分析方法已经被证明是进行板弹簧性能分析的有效方法［3-6］。本文以外圆直径为120 mm的板弹簧为例，通过改变弹簧厚度、涡旋角、涡旋槽个数以及涡旋槽宽度这4个参数来分析板弹簧的应力分布及刚度大小，其整个计算过程如下:

(1)前处理阶段:建立几何模型、选择求解类型、输入材料特性及划分网格。利用AutoCAD和Inventor绘图软件绘制板弹簧的三维结构，为了提高有限元网格的质量，计算中省去了对分析无影响的安装中心孔及外圆安装孔。随后将其导入ANSYS有限元软件。此分析为静态结构分析，材料选择为普通的结构钢，其弹性模量为200 GPa，泊松比为0.3，模型采用自用网格划分，如图1所示。

图1 板弹簧的有限元网格划分Fig.1 Flexure spring meshing results

(2)求解阶段:设置边界条件、加载及求解。根据弹簧的使用过程中所受到的实际载荷情况对其加载:

1 )在板弹簧外圆与垫片的接触面进行位移约束，该接触面各方向位移为0;

2 )对板弹簧中心垫片施加位移约束，使其X、Y向固定，Z向即垂直于接触面的方向施加1—10 mm的位移载荷，计算板弹簧在不同位移载荷下的应力分布;

3 )在板弹簧中心垫片上不施加位移载荷，而是施加轴向力的载荷，值为1—5 N，计算板弹簧的轴向刚度值。

(3)后处理阶段:在弹簧中心施加位移载荷时，主要求解板弹簧的应力分布，在板弹簧中心垫片上施加轴向力时，主要求解板弹簧的变形结果，以确定其轴向刚度值。

3 计算结果分析

3.1 板弹簧的应力分布结果

本文对8种不同参数组合下的板弹簧进行了有限元分析，每种参数组合的代号用A-B-C-D表示，其中A为板弹簧的涡旋角，B为板弹簧的厚度，C为涡旋槽个数，D为涡旋槽宽度，如440-0.5-3-1表示该板弹簧的涡旋角是440°，厚度为0.5 mm，涡旋槽个数为3，涡旋槽宽度为1 mm。

图2为440-0.5-3-1板弹簧在轴向位移为10 mm时的应力分布图，从图中可以看出最大应力发生在涡旋槽尾部，达到435.35 MPa。图3为8种参数组合下板弹簧的最大应力随轴向位移的变化曲线。从图中可以得出以下结论:

图2 440-0.5-3-1板弹簧在轴向位移为10 mm时的应力分布图Fig.2 Stress distribution of 440-0.5-3-1 springwhen axial displacement is 10 mm

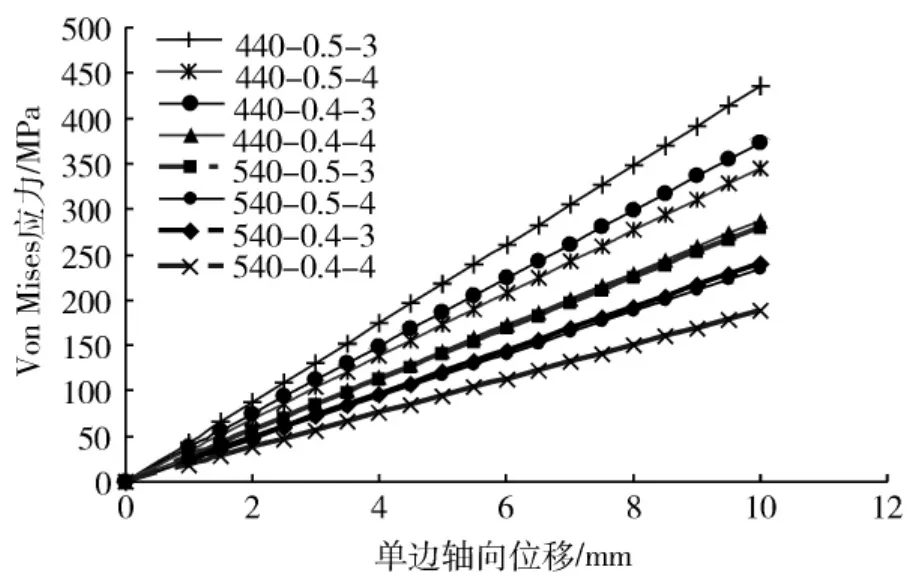
图3 不同参数条件下最大应力随轴向位移的变化曲线Fig.3 Curve of maximum stress versus axial displacement with different parameters

(1)板弹簧的最大应力与其所受的轴向位移载荷成正比;

(2)在其它参数相同的情况下，涡旋角为440°的板弹簧最大应力要远大于涡旋角为540°的板弹簧。结果显示，440-0.5-3-1在轴向位移为10 mm时，最大应力为435.35 MPa，而540-0.5-3-1仅为279.64 MPa;

(3)其它参数相同的情况下，板弹簧最大应力随板弹簧厚度的增大而增大，如440-0.5-3-1板弹簧在轴向位移为10 mm时的最大应力为435.35 MPa，而440-0.4-3-1板弹簧的最大应力为373.15 MPa。

3.2 板弹簧的刚度分析结果

通过在与板弹簧中心接触的垫片平面上加载力的载荷，分析得出该处位移，根据公式(1)计算出板弹簧刚度:

其中:K为板弹簧轴向刚度，F为所受轴向力的载荷，S为板弹簧在轴向载荷处的最大位移。

图4为540-0.5-3-1板弹簧中心圆面上受1 N轴向力时的变形图，从图中可以看出它的中心处变形最大，变形量沿径向向外逐渐减小，变形最大值为6.708 6 mm。图5为8种不同参数组合下板弹簧位移量随轴向力的变化曲线，通过计算得出这8种条件下板弹簧的刚度值，见表1。

图4 540-0.5-3-1板弹簧在受轴向力为1 N的载荷时的变形图Fig.4 Deformation of 540-0.5-3-1 spring when axial displacement is 1 N

从表1的计算结果中可以得出以下结论:

(1)在其它参数不变的情况下，涡旋角增大其刚度减小，如440-0.5-3-1板弹簧的刚度为0.468 8 N/mm，而540-0.5-3-1板弹簧的刚度仅为0.289 1 N/mm。

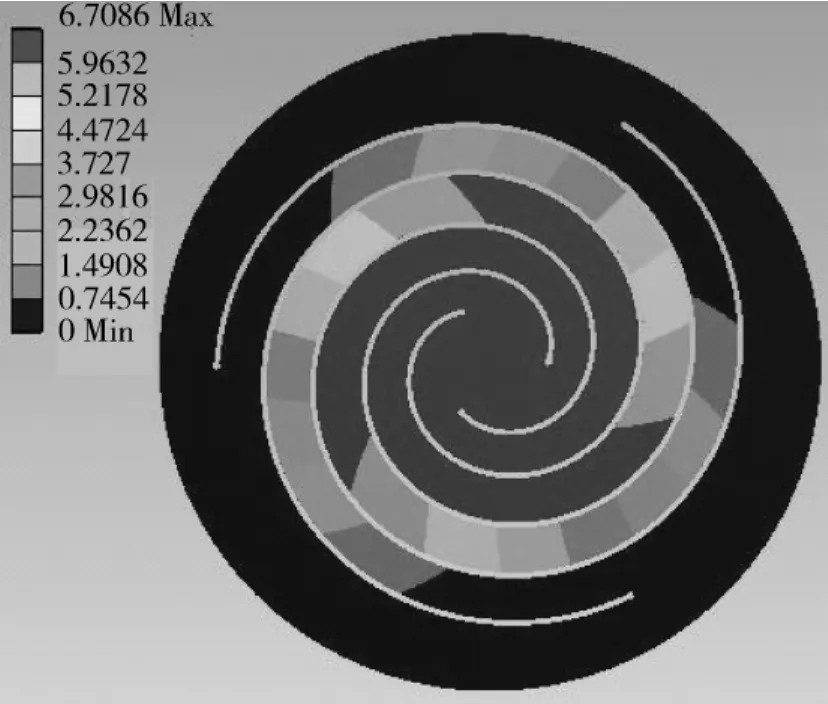
图5 不同参数条件下位移随载荷力的变化曲线Fig.5 Curve of axial displacement versus axialforce with different parameters

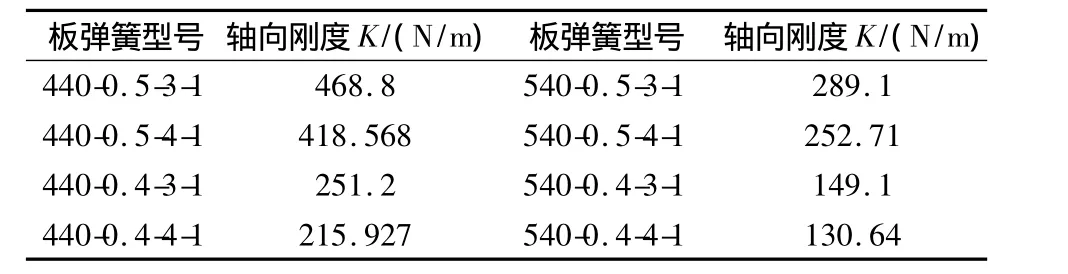
表1 各型号板弹簧轴向刚度值Table 1 Value of axial stiffness of flexure springs

(2)在其它参数不变的情况下，板弹簧刚度随其厚度的增大而增大，本分析中440-0.5-3-1板弹簧的刚度为0.468 8 N/mm，而440-0.4-3-1板弹簧的刚度仅为0.251 2 N/mm。

(3)涡旋槽个数为4的板弹簧刚度值小于个数为3的板弹簧，结果显示，440-0.5-4-1板弹簧刚度为0.418 568 N/mm，而 440-0.5-3-1板弹簧的值为0.468 8 N/mm。

3.3 刚度应力比的结果

在设计板弹簧时，刚度和应力最大值是需要考虑的最重要的两个因素，即板弹簧的刚度越大越好，受相同位移载荷时其应力最大值越小越好。一般情况下，板弹簧的刚度越大，受相同轴向位移载荷时它的应力最大值就越大，也就是说板弹簧刚度的增大是以增大其最大应力值为代价的，而最大应力直接影响板弹簧的使用寿命，因此在同一位移载荷下，同一外径尺寸的板弹簧刚度不能一味的增加。通过以上分析可知，板弹簧的好坏不能单一的通过比较其刚度和最大应力值的大小而定，而是应该用二者的比值来评价，即刚度应力比，该值越大说明该板弹簧的设计就越合理。

本文计算了板弹簧涡旋槽宽度对其刚度应力比的影响。该分析中，板弹簧的涡旋角为440°，厚度为0.5 mm，涡旋槽个数为3。刚度应力比随板弹簧的蜗旋槽宽度的变化曲线如图6所示。

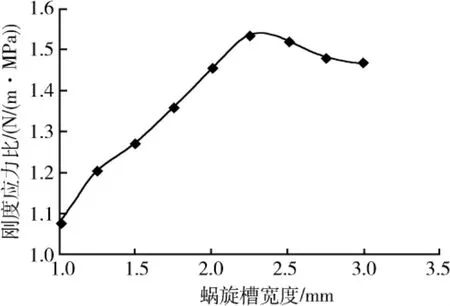
图6 刚度应力比随涡旋槽宽度的变化曲线Fig.6 Curve of stiffness-stress ratio versus spiral slot width

从图中可以看出，随着蜗旋槽宽度的增大刚度应力比的值先增大后减小，在槽宽为2.25 mm时达到峰值1.536 531 N/(m·MPa)。即在刚度和最大应力值满足许用条件的情况下，该尺寸板弹簧的涡旋槽宽设计最为合理。

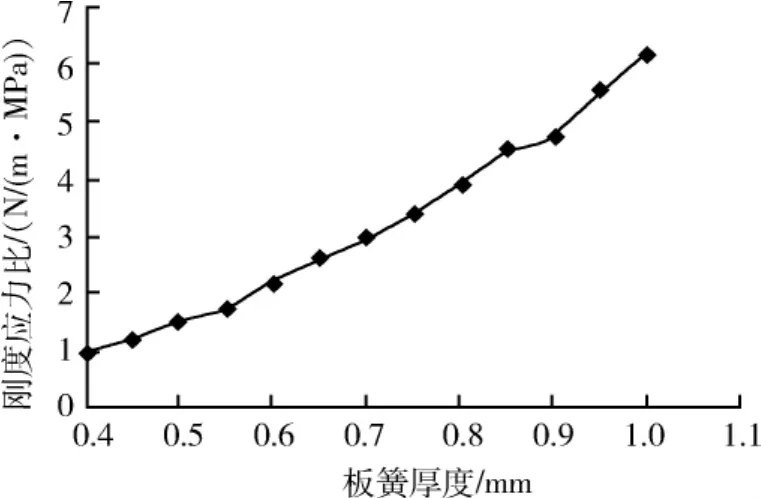
图7 刚度应力比随板弹簧厚度的变化曲线Fig.7 Curve of stiffness-stress ratio versus spring thickness

此外，研究也计算了厚度对其刚度应力比的影响。该分析中板弹簧的涡旋角为440°，涡旋槽个数为3，涡旋槽宽度为2.25 mm。通过计算得出，板弹簧厚度为1 mm的刚度大约是0.4 mm时的15倍，而应力最大值仅提高到原来的2.5倍左右，这一结论也可以通过刚度应力比的值来进行说明。图7为其它条件不变的情况下，刚度应力比随板弹簧厚度的变化曲线。该图表明，随着板弹簧厚度的增大，其刚度应力比也随之增大，厚度为1 mm时板弹簧的刚度应力比为6.145 541 N/(m·MPa)，大约是0.4 mm厚板弹簧的5倍。因此可以认为，提高板弹簧厚度，是提高板弹簧刚度的有效途径。在最大应力满足许用应力的条件下，板弹簧厚度越厚，它的设计就越合理。

4 结论

通过对外径为120 mm的8种不同参数组合的板弹簧进行的有限元计算，得出了每个型号下板弹簧的应力分布情况和轴向刚度值的大小。通过单独对板弹簧涡旋槽宽度和板弹簧厚度进行的有限元分析，得出以下结论:

(1)随着板弹簧涡旋槽宽度的增加，刚度应力比先增大后减小，在宽度为2.25 mm时达到最大值，即在满足板弹簧材料的屈服应力的情况下，该涡旋槽宽度最为合理。

(2)随着板弹簧厚度的增大，其刚度应力比也逐渐增大，当板弹簧厚度达到1 mm时达到最大值，表明在满足板弹簧材料的屈服应力的情况下，板弹簧厚度越大设计越合理。

1 祁影霞，陈 曦，张 华，等.斯特林制冷机中膜片弹簧的有限元可视化分析［J］.低温与超导，2009，37(3):8-11.

2 陈 楠，陈 曦，吴亦农，等.涡旋柔性弹簧型线设计及有限元分析［J］.中国机械工程，2006，17(12):1261-1264.

3 Chen N，Chen X，Wu Y N，et al.Spiral profile design and parameter analysis of flexure spring［J］.Cryogenics，2006，46(6):409-419.

4 Gaunekar A S，Goddenhenrich T，Heiden C.Finite element analysis and testing of flexure bearing elements［J］.Cryogenics，1996，36(5):359-364.

5 Wong T E，Pan R B，Johnson A L.Novel Linear flexure bearing［J］.Cryocoolers，1992(7):675-698.

6 Marquardt E，Radebaugh R，Kittel P.Design equations and scaling laws for linear compressors with flexure springs［J］.Cryocoolers，1992(7):783-804.

Finite element analysis of flexure spring in pulse tube cooler

Li Jianguo1，2Yan Tao1Cai Jinghui1

(1Key Laboratory of Space Energy Conversion Technologies，Technical Institute of Physics and Chemistry，Chinese Academy of Science，Beijing 100190，China)
(2Graduate University of Chinese Academy of Sciences，Beijing 100190，China)

An analysis was carried out on the stress and axial stiffness of flexure springs with 120 mm diameter using the finite element analysis software.A relationship was obtained between the performance of flexure spring and its geometrical parameters including spring thickness，spiral angle，number of spiral slot width.A concept of stiffness-stress ratio was proposed as the evaluation criteria of the performance of flexure spring，which can serve as the foundation of spring design.

pulse tube cooler;flexure spring;finite element analysis

TB651

A

1000-6516(2012)01-0040-04

2011-11-16;

2012-01-20

李建国，男，30岁，博士研究生。