三维纤维过滤介质压力损失数值模拟

徐芳芳，付海明，雷泽明，甘 灵

（1.东华大学 环境科学与工程学院，上海 201620；2.中建三局建设工程股份有限公司，湖北 武汉 430000）

压力损失是纤维过滤介质的重要参数之一.当纤维多孔介质内的流体流速较低或者雷诺数（Re）较小时，一般假设其流场服从经典的达西定律，即压力梯度和平均速度存在线性关系.随着Re增加到一极限值时，其不再服从达西定律，多孔介质内的流体流动由于惯性及黏性等作用呈现非线性趋势[1].VAFAI[2]是较早研究达西定律扩展现象的研究者之一，其使用宏观平均技术来研究达西定律中的摩擦阻力和惯性阻力，认为这些非线性的影响使得压力损失比达西定律得到的要高.基于刚性多孔介质的一维稳态不可压缩层流来求解Navier-Stokes（N-S）方程，文献[3]提出一个包括非达西影响的修正表达式.DEIBER等[4]考虑了黏性和惯性影响，采用涡量流方程，研究了高Re下多孔介质的自然对流.文献[5]通过成堆马铃薯的压力损失－速度关系试验，验证了Forchheimer方程的有效性，并利用有限元素 方 法 对 三 维 的 Darcy-Forchheimer-Brinkman（DFB）模型进行数值求解，结果表明该模型的计算结果与压力损失的试验数据一致.文献[6]基于达西拓展方程，使用有限体积方法，模拟了多孔介质表面存在液滴时的影响.YANG等[7]基于DFB方法，模拟了饱和多孔介质内的流体流动，得出Re与速度一样，都是影响压力损失的重要因素.但有些研究者认为，Forchheimer方程仅在高Re时有效，而在达到完全发展的紊流阶段前，还应该存在过渡流.MEI等[8]通过严密的理论推导，给出了各向同性介质压力损失的三次方表达式.ANDRADE等[9]通过对试验数据的整理，采用速度的三次方对Forchheimer方程进行修正，用以描述非达西现象.CAI等[10]利用波尔兹曼格子法，给出了二维简化多孔介质的三次方及过渡区的表达式.虽然这些研究结果对于非达西现象的研究很有应用价值，但其都是建立在一维或二维的简单多孔介质模型上的，这对真实的纤维多孔介质而言，并不适用.因为纤维多孔介质的流场发生在三维空间，且纤维一般是随机排列的.另外，Forchheimer方程中的系数理论上难以给出，一般需通过试验数据得到，且给出值通常随不同研究者或不同的多孔介质模型而不同[11].随着计算机技术的发展与计算能力的提高，非达西流的数值研究得到较大的发展.本文基于VBA程序语言，创建了一系列三维随机排列纤维的多孔介质模型，采用计算流体动力学（CFD）软件模拟了孔隙尺度下纤维多孔介质模型内部的气相流场，并将模拟数据与一些经验关系式得到的结果进行比较，最后通过数据拟合得到一个可以描述非达西现象的表达式.

1 多孔介质的经验模型

多孔介质的不可压缩流可以通过两种方法来描述：一种是孔隙尺度下求解N-S方程；另一种是直接求解平均方程或已存在的经验方程式[10].由于多孔介质几何的复杂性和不规律性，直接在孔隙尺度下求解N-S方程式，计算量大且很难得到精确的计算结果.通常对多孔介质进行简化，忽略其复杂性，得出相应的经验公式并应用于工程方面.但这些简化模型往往是基于经验假设，并不适合用来研究多孔介质内复杂的流动情况.事实上，这两种方法之间并不是相互独立的.

由于Re与速度都是影响压力损失的重要参数[10].故可将广泛使用的Re作为标准，直观地研究非达西现象中的流动情况，其中，Re为惯性力与黏性力的比值.

其中：ρ为流体密度；为流体平均速度；μ为流体动力学黏度；Df为纤维直径，在本文中作为特征长度.假设纤维多孔介质流动分为线性达西流区以及非线性流区两个不同的区域，分别研究其流动特性.

（1）线性达西流区：在这一区域内，流场流动符合达西定律，其压力梯度－速度表达式如式（2）所示.

其中：Δp为流体的压力损失；K为渗透率；L为过滤介质厚度.为了直观地表述惯性的影响，转变式（2）为式（3）所示.

其中：Ke为有效渗透率；c为常数.在线性达西流区域内，黏性力占主导地位.

（2）非线性流区：在这一区域内，随着Re不断增加，多孔介质的流动可用Forchheimer方程进行描述[3].

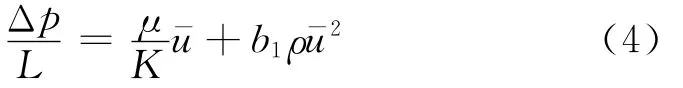
其中：b1为非达西流系数，其值与孔隙尺寸、形状和孔隙率有关；方程右边的第一、二项分别为黏性力和惯性力.对式（4）进行变换得如式（5）所示的Forchheimer方程.

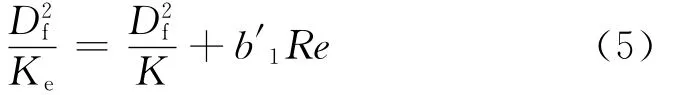
其中：b′1＝b1Df，为一无量纲参数.在非线性流区域内，惯性力影响比黏性力影响大，流体行为主要受惯性力支配.

2 数值模拟计算

2.1 三维随机纤维过滤介质模型的建立

本文中基于VBA语言开发技术和AutoCAD平台，采用随机算法生成三维纤维多孔介质.在模型生成过程中，长方体代表纤维多孔介质材料，细圆柱体代表纤维.通过输入恰当的参数（如纤维的长、宽及纤维的直径、数量），即可得到相应孔隙率的模型.需要注意的是，为了生成高质量的网格，模型中不允许纤维间相互接触.因此，在模型生成过程中，忽略纤维的弯曲、压延及生产过程中造成的变形.

2.2 模型的网格划分及边界条件

图1给出了本文的计算模型及相应的边界条件.假设气体通过速度入口进入计算区域，然后从压力出口流出计算区域.在本文中，为了消除纤维面较强流速或压力梯度的影响，入口边界和出口边界分别位于距离过滤器上游10倍于纤维直径和下游5倍于纤维直径处[12].由于流体流动主要在纤维厚度方向，侧边的边界条件对模拟结果的影响小，因此，计算域的侧边采用对称性边界条件.另外，对于纤维表面的流体，本文假设为无滑移边界.

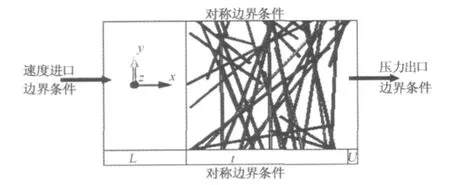
图1 数值模拟区域及边界条件Fig.1 Numerical simulation area and boundary conditions

在给出压力损失的模拟结果前，需确保模拟结果独立于所划分的网格.为此，本文计算了纤维多孔介质的填充率（α）为4.51%的模型在不同的纤维边界网格尺度数及总网格数量下的压力损失.改变纤维周边的网格尺度数，将其由9开始减小至2，得网格尺度数对压力损失的影响结果如图2所示.由图2可以看出，降低网格尺度数开始会导致压力损失增加，至一定程度（纤维网格边界尺度数小于2.5）后，压力损失几乎没有变化.

总网格数对压力损失的影响如图3所示.由图3可以看出，增加总网格数量，开始时压力损失逐步增加，但当总网格数超过2×106时，压力损失几乎

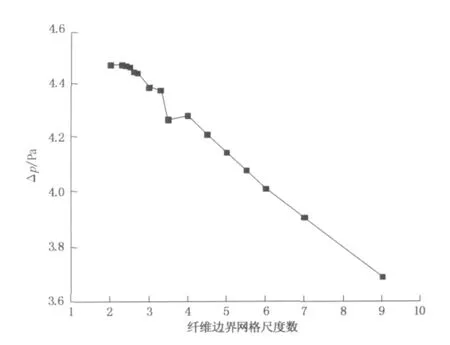
图2 纤维边界网格尺度对压力损失的影响Fig.2 Effect of fiber boundary mesh size on pressure drop

没有变化.因此，在本文的数值模拟计算中，所有模型的计算工况均选择网格尺度数为2.5和总网格数为2×106，以保证计算结果的准确性.另外，本文涉及的所有多孔介质模型中的纤维直径为16μm，过滤介质厚度为5mm；纤维介质尺寸为500μm×500 μm×200μm.

图3 纤维边界网格数量对压力损失的影响Fig.3 Effect of fiber boundary mesh numbers on pressure drop

3 模拟结果与讨论

3.1 流体流动分析

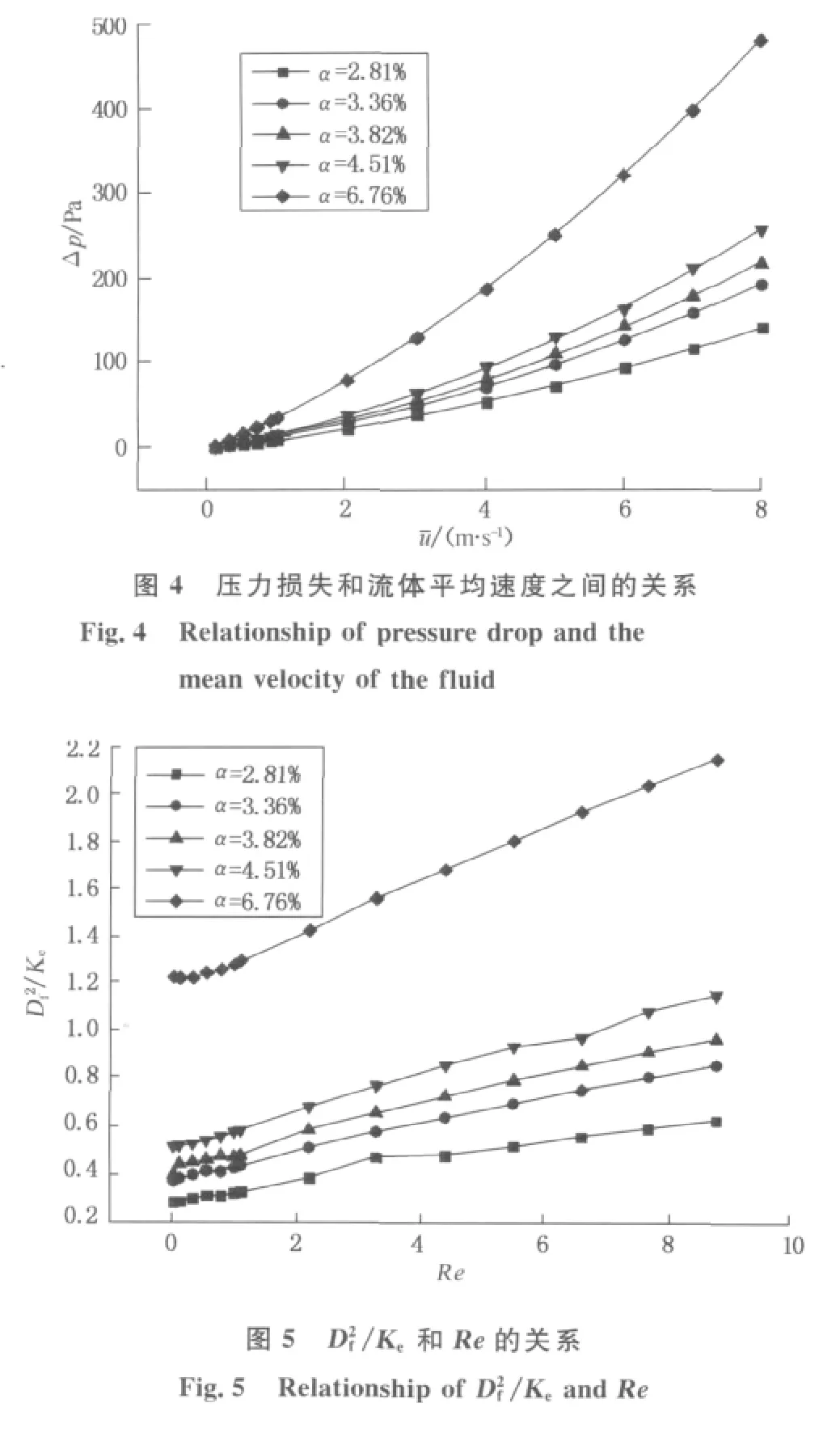
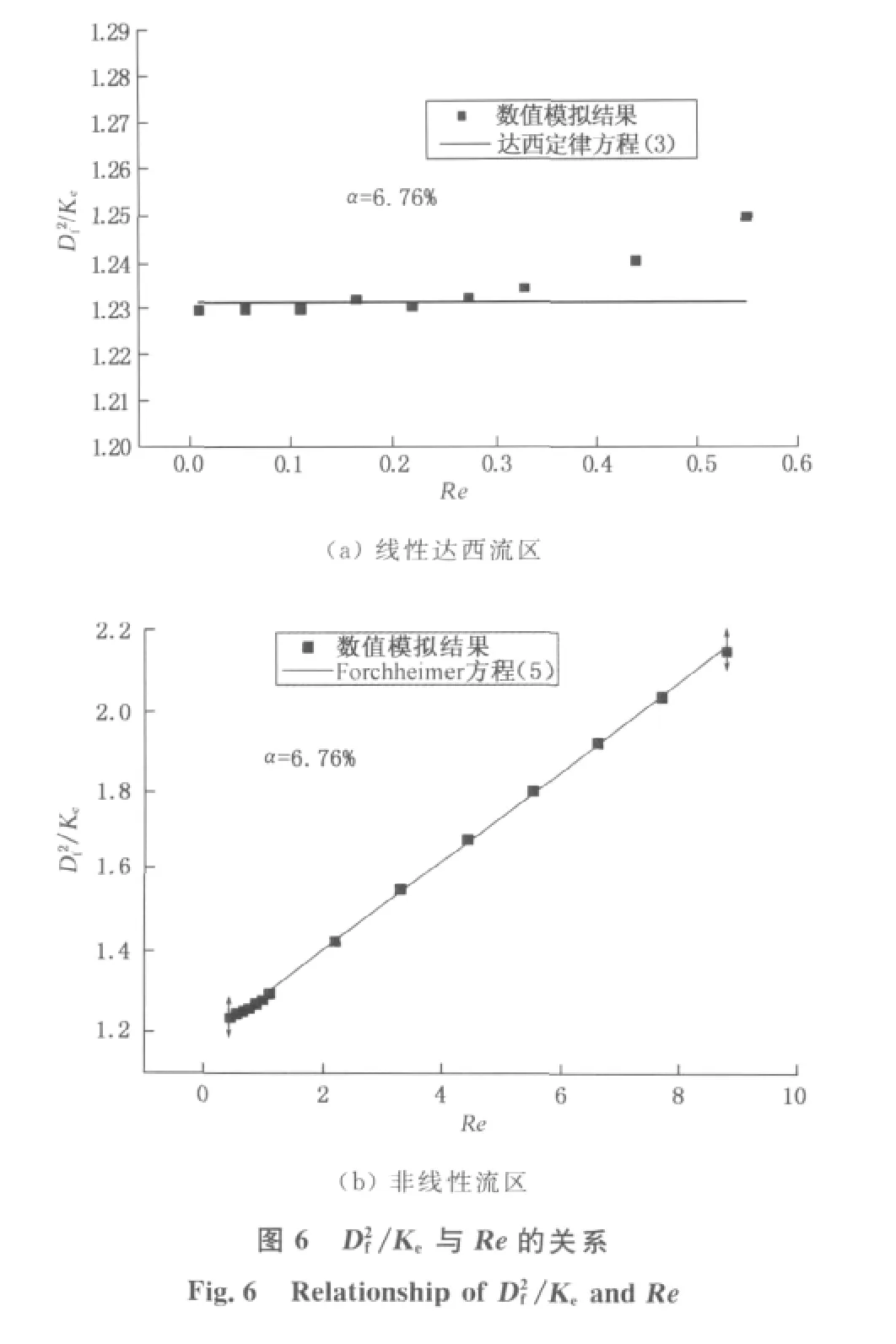
根据模拟计算，得出不同α下随机排列的三维纤维多孔介质的压力损失与流体平均速度的关系如图4所示.同样，为了更好地观察到惯性的影响，将压力梯度－流体平均速度关系转化为有效渗透率与Re的关系（如式（5）），并绘出D2f／Ke与Re的关系曲线如图5所示.从图4和5可以清楚地看出，随着流体平均速度或Re的增加，纤维过滤多孔介质内的压力损失逐渐增加，但这种增加是非线性的，因此，单纯用达西定律来描述该模型下的流场是不合适的.值和由式（5）得出的K的计算值，发现所得值有些不同，但是两者之间的差异非常小，最大相对误差不超过4%.因此，式（5）可以精确地描述非线性流区的流动规律.

选择其中一种模型（α＝6.76%）的模拟结果（如图6所示），具体分析纤维过滤介质有效渗透率与Re的关系.由图6（a）可以看出，当Re≤0.33（对应的流体平均速度为0.3m／s）时，有效渗透率与Re的比值几乎为一常数.数值模拟结果与达西定律表达式非常吻合，该模拟区域为线性达西流区.由图6（b）可以看出，Re足够大时，其与纤维过滤介质有效渗透率之间的比值不再是常数，即数值模拟结果不再符合达西定律.将数值模拟结果与Forchheimer方程对比发现，模拟结果可以用Forchheimer方程来预测，该模拟区域为非线性流区.

分别比较由式（3）推算出的不同α下渗透率K

3.2 压力损失－速度关系式

分别模拟计算5种纤维多孔介质填充率（α分别为2.81%，3.36%，3.82%，4.51%，6.76%）和7种迎面风速下（分别为0.008 3，0.050 0，0.100 0，0.150 0，0.200 0，0.250 0，0.300 0m／s）的流场分布情况，并依据这35组数据结果进行分析，以方程K＝D2f／[aα3／2（1＋bα3）]为基础，a和b为待定系数，可得出任意分布纤维多孔介质渗透率表达式如式（6）所示[13].

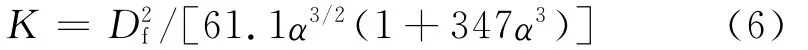
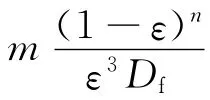
结合数据拟合软件，得出系数b1的表达式如式（7）所示.

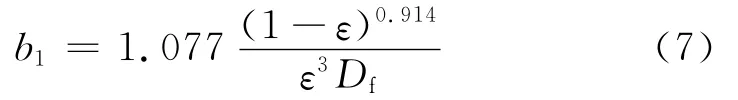
将现有模拟结果与文献[14-15]的结果进行比较，结果如图7所示（本文的Df与文献[14-15]的Df统一为定值）.由图7可以看出，文献[14]提出的表达式往往过高地估计系数b1值，而文献[15]给出的关系式往往低估了系数b1值.

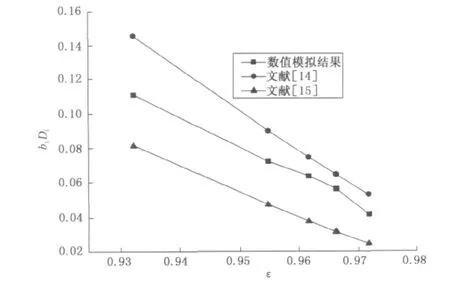
图7 b1Df与ε的关系曲线Fig.7 Relationship between b1Dfandε

综上所述，随着Re的增大，达西定律出现偏差，这主要是由于惯性力的影响，使得随机纤维多孔介质流动出现不同的流动区域.本文最后得到的适合非达西现象的压力损失拓展表达式如下所述.

线性流区（≤0.3m／s）：

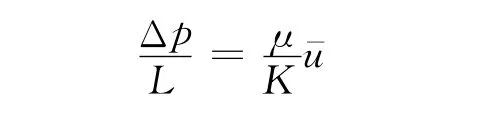
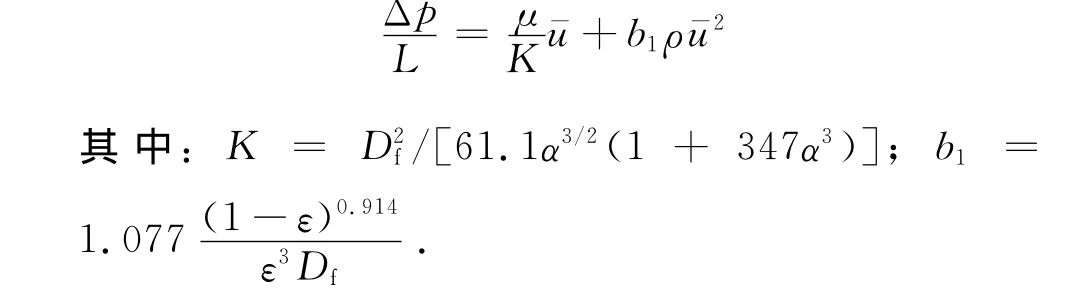
4 结 语

本文通过创建随机排列的三维纤维过滤介质微观结构模型，采用计算流体动力学软件模拟计算不同流体平均速度及多孔介质填充率条件下三维纤维过滤介质内部的气相流场，得出如下主要结论.

（1）在本文建立的模型中，当Re≤0.33或当≤0.3m／s时，达西定律可以精确地描述纤维过滤多孔介质的流场，即压力损失与速度呈线性关系；而随着Re或速度逐渐增大，压力损失随着其增大呈现出非线性增加，则达西定律不适用于描述此时的流体流动.

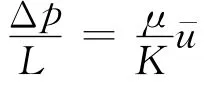
参 考 文 献

[1]HAO Z Y，CHENG N S，TAN S K.Investigation of inertial effect in simplified porous media flow[J].Advances in Water Resources and Hydraulic Engineering，2009，1：160-165.

[2]VAFAI K.Convection flow and heat transfer in variable porous media[J].Journal of Fluid Mechanics，1984，147：233-259.

[3]FORCHHEIMER P.Wasserbewegung durch Boden[J].Zeitschrift Verein Deutscher Ingenieure，1901，45：1782-1788.

[4]DEIBER J，BORTOLOZZI R.A two-field model for natural convection in a porous annulus at high Rayleigh numbers[J].Chemical Engineering Science，1998，53（8）：1505-1516.

[5]VAN DER SMAN R G M.Prediction of airflow through a vented box by the Darcy-Forchheimer equation[J].Journal of Food Engineering，2002，55（1）：49-57.

[6]JR REIS N C，GRIFFITHS R F，SANTORS J M.Numerical simulation of the impact of liquid droplets on porous surfaces[J].Journal of Computational Physics，2004，198（2）：747-770.

[7]YANG D X，YANG Y P，COSTA V A F.Numerical simulation of non-Darcian flow through a porous medium [J].Particuology，2009，7（3）：193-198.

[8]MEI C C，AURIAULT J L.The effect of weak inertia on flow through a porous medium[J].Journal of Fluid Mechanics，1991，222：647-663.

[9]ANDRADE J S，COSTA U M S，ALMEIDA M P，et al.Inertial effects on fluid flow through disordered porous media[J].Physical Review Letters，1999，82（26）：5249-5252.

[10]CAI Z H，SHI B C，LU J H，et al.Non-Darcy flow in disordered porous media：A lattice Boltzmann study[J].Computers ＆ Fluids，2010，39（10）：2069-2077.

[11]TENG H，ZHAO T S.An extension of Darcy＇s law to non-Stokes flow in porous media[J].Chemical Engineering Science，2000，55（14）：2727-2735.

[12]HOSSEINI S A，VAHEDI TAFRESHI H.3-D simulation of particle filtration in electrospun nanofibrous filters[J].Powder Technology，2010，201（2）：153-160.

[13]李艳艳.纤维过滤材料结构参数优化数值模拟[D].上海：东华大学环境科学与工程学院，2011：20-22.

[14]ERGUN S.Fluid flow through packed columns[J].Chemical and Engineering Progress，1952，48（2）：89-94.

[15]LEE S L，YANG J H.Modelling of Darcy-Forchheimer drag for fluid flow across a bank of circular cylinders [J].International Journal of Heat and Mass Transfer，1997，40（13）：3149-3155.