基于Wold模型的织物起球纹理非确定性成分提取

徐增波，周 胜

（1.上海工程技术大学 服装学院，上海 201620；2.扬州市职业大学 纺织服装系，江苏 扬州 225009）

织物表面抗起球等级是纺织品性能评估中的一项主要指标，如何客观准确地把握起球等级是近年来一直研究的课题，比较集中的研究方向是采用计算机视觉评估方式，如应用图像分析[1－6]、切面投影[7－8]或体视重建[9]等途径提取出反 映 起 球 等 级 的特征指标，其中图像分析方法因其设备简易、操作方便而应用最为广泛，但一般织物表面都有规则的周期性纹理，多数情况下该纹理会严重干扰织物表面起球特征指标提取，如何合理滤除织物表面规则或准规则纹理，是提取织物表面毛球信息之前必须要解决的问题.

FRANCOS等[10]通过对自然纹理特征的研究提出了基于Wold分解的纹理模型，即对于任一满足二维同质随机场的纹理图像，其总可以分解为相互正交的确定性成分和非确定性成分.确定性成分又可进一步分解为相互正交的谐波成分和单方向奇异的短暂（evanescent）成分.该模型在纹理数据库检索、纹理分割、纹理恢复等[10－16]中已得到较好应用，并且模型中的确定性和非确定性成分模型可与其他模型结合（如Gabor函数、GMRF模型等），进行纹理检索和分类等[17].对于织物起球纹理图像，其Wold纹理模型中的确定性成分对应于织物纹理中周期性和方向性规则纹理，非确定性成分即为滤除织物纹理底纹后起球纹理图像.

FRANCOS等提出最大似然参数估计法[18]和谱分解法[10]进行谱分解.最大似然估计法的精度虽然较高，但计算量大，且当谱中含有很多峰值结构或这些结构相对于周围区域谱幅值不是很高时尤为突出.谱分解法的计算效率虽然较高，但它的频谱单一阈值方法对多数纹理确定性成分抽取缺乏鲁棒性，因为谱中一些奇异峰结构只是局部极大而非全局最大.此外纹理周期图中一些谐波峰结构通常是一个围绕该点的扩展区域，且不同扩展区域的谐波点傅里叶幅值强度也不同，所以单一阈值法不能满足扩展区域幅值变化的要求.LIU等[11]用5×5邻域局部最大值方法来搜寻频谱对称半平面中的极值点，并利用谐波和基频之间的关系对之进行取舍，但这种方法计算相对繁琐，特别是对很多谐波扩展平坦区域，谐波点确定精度不够.YONG等[16]用高价谱（HOS）抽取 Wold模型中确定性成分，其谐波抽取方法与文献[11]存在同样缺陷.

本文针对起球织物纹理的Wold谱分解特点，采用了适合于傅里叶幅值图中奇异峰结构（点、线及其扩展区域）幅值局部变化的检测算法，自适应提取织物起球纹理图像中的确定性成分，算法流程如图1所示，即先设计一定的算法对频谱中局部极大点状峰结构中心点进行检测，然后再进行线状峰结构中心线检测，之后设计一定标准估计这些中心频率的扩展区域大小，作为最后确定性成分的奇异峰结构区域.

图1 Wold谱分解算法流程Fig.1 Flow of the spectral Wold decomposition algorithm

在奇异峰结构检测中，本文纵观多幅织物纹理图像的傅里叶幅值图发现，织物中规则排列纱线在频谱中的峰结构（即为纹理中的确定性成分）与二维高斯函数分布非常接近，峰结构中心近似于高斯函数顶点（基频或谐波），其扩展区域近似于高斯函数发散部位（准谐波频率）.检测点状峰结构就等同于检测类似二维高斯函数幅值分布的局部区域（简称二维高斯目标），然后以该区域极大值点所对应频率作为点状峰结构中心频率，且不必再计算这些中心点频率间的关系.一般对于二维高斯目标检测，只要设计与该目标匹配滤波器进行相关检测，再根据输出值识别目标即可.然而傅里叶幅值谱中分布的高斯目标强度及大小随着图像中纹理谐波分量的变化而变化，即其中可能含有各种局部强弱及大小的高斯目标，单一尺寸的匹配滤波器不可能满足多形态高斯目标检测要求，所以本文采用多尺度B－样条小波匹配滤波器[1，19]进行奇异峰结构检测.

1 Wold分解理论简介

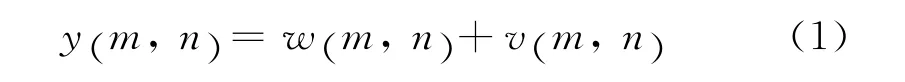
其中：｛w（m，n） ｝为二维纯非确定性和规则随机场；｛v（m，n）｝为二维确定性随机场，可进一步被唯一正交分解为

其中：｛p（m，n）｝为一半板（NHSP）确定性谐波随机场（周期性规则纹理）；｛g（m，n）｝称为广泛短暂随机场（方向性规则纹理），它是由有限数量相互正交短暂场线性组合而成.

在频域中，以F（ω，υ）表示 ｛y（m，n）｝的谱分布函数，并令Fs（ω，υ）表示F（ω，υ）的奇异部分，则F（ω，υ）＝Fw（ω，υ）＋Fv（ω，υ），其中非确定性随机场谱分布函数Fw（ω，υ）为非奇异的；Fv（ω，υ）＝Fp（ω，υ）＋Fg（ω，υ），其中Fp（ω，υ）和Fg（ω，υ）分别为 ｛p（m，n）｝和 ｛g（m，n）｝的谱分布函数，在谱中分别对应为点状和线状奇异支撑域.

3种不同Wold成分的织物纹理图像及其频域示意图如图2所示，其中，上行为含有谐波成分的周期性纹理图像，在傅里叶幅值图中表现为点状区域支撑的谱峰结构；中间行为含有短暂成分的方向性纹理图像，在傅里叶幅值图中表现为线状区域支撑的谱峰结构；下行为不含任何确定性成分的纹理图像，在傅里叶幅值图中表现为相当光滑的谱结构.

图2 3种不同Wold成分的织物纹理图像及其频域分割示意图Fig.2 Examples of fabric pilling textures with different Wold components

2 Wold分解算法设计

2.1 谐波点状峰结构的中心点检测

2.1.1 匹配滤波器设计

首先对二维奇异峰结构高斯目标（式（3））和背景纹理（式（4）和（5）分别为可分离和不可分离马尔科夫噪声模型）进行建模表征.

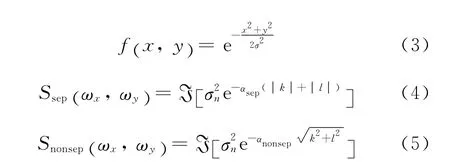
其中：ℑ为傅里叶变换.

假设在背景噪声为n（x，y）、功率谱为Snn（x，）的图像中有一确定性目标f（x，y），位于（x0，y0）处， 按 照 最 大 信 噪 比 准 则，检 测f（x，y）的最优滤波器hMF（x，y）的频域表达式为具有如式（6）所示传输函数的预白化匹配滤波器.

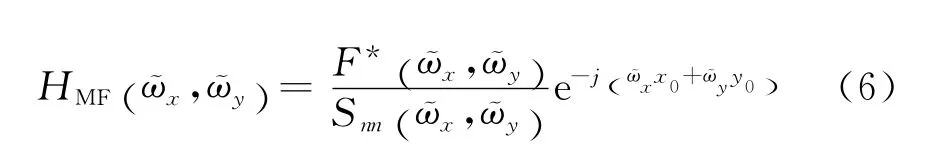
这里F（x，y）为f（x,y）的傅里叶变换.式（6）对应可分离和不可分离匹配滤波器传输函数（α≪1）分别为

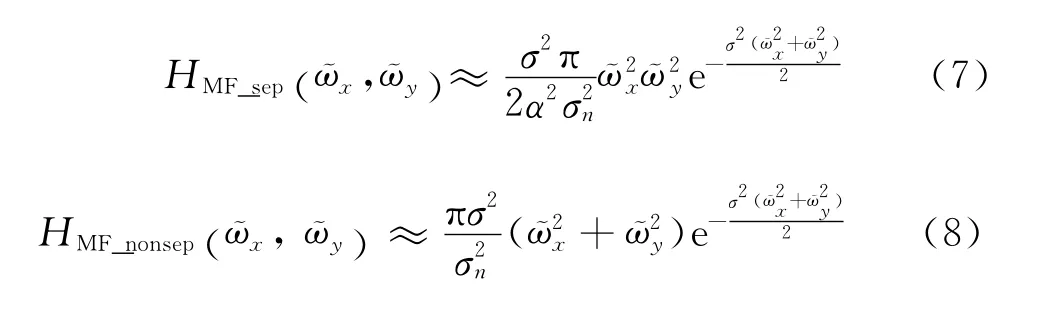
2.1.2 小波多尺度匹配滤波器设计

根据B－样条函数理论，B-样条βn（x）与高斯函数具有很好的近似性：

这里选用具有对称性的B－样条二阶导数作为样条小波（如式（11）所示），并利用二进样条函数与小波之间的两尺度关系得到式（10）～（12）.

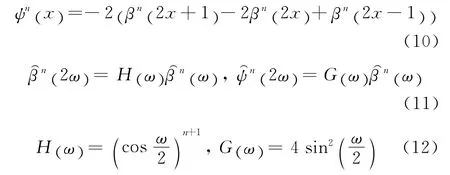
根据二维小波函数的定义及其平滑函数与水平、垂直及对角方向小波函数对应两尺度关系有

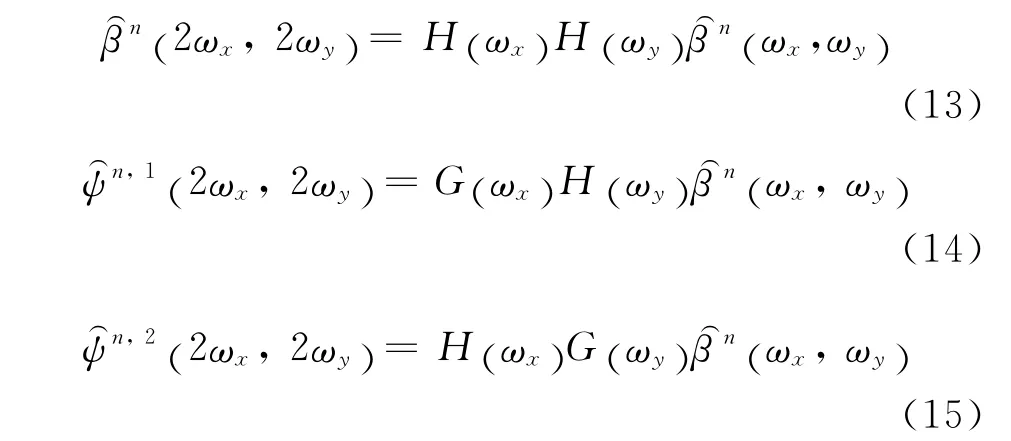
其中：G3（ωx，ωy） 及G1，2（ωx，ωy）与 式 （7）和 （8）非常近似，可以替代之进行高斯目标匹配滤波检测.

根据构造的二维B－样条小波及二维Mallat分解原理[20]，重新构造用于检测高斯目标的二维多尺度匹配滤波器组，通过匹配滤波器组各通道的目标检测分割及融合，最终检测并定位出高斯目标[1，19].

图2（b）中周期性结构纹理傅里叶幅值图的二维高斯目标匹配滤波各通道能量输出图如图3所示，其中上行为不可分离滤波匹配输出图，下行为可分离匹配滤波结果输出图.图4为各通道目标检测结果融合图及其谐波点状峰结构中心频率点图.

图3 周期性结构纹理傅里叶幅值图的多尺度样条小波匹配滤波检测结果Fig.3 Matched filtered results using multiscale B-spline wavelets transform on discrete Fourier transform magnitudes with strong harmonic peak regions

2.2 线状峰结构中心线检测

本文采用基于方向投影的Radon变换[21]来进行傅里叶幅值图线检测.在Radon变换前先抽取出其中的谐波支撑区域，以减少其在投影变换矩阵中对线特征抽取的干扰.Radon变换投影矩阵中的局部奇异区域对应于傅里叶幅值图中某一旋转角投影角度上的线区域，该奇异区域的大小和形状由线区域的形状决定.图5（a）为图2（b）中方向性规则纹理的傅里叶幅值图的Radon变换图.Radon变换图像中线特征点提取也是局部奇异性区域提取问题，其最大点提取采用与频谱谐波点抽取相同的途径，图5（b），5（c）及5（d）分别为图5（a）中局部奇异目标检测、线特征点分布及其Radon逆变换.

2.3 峰结构中扩展区域估计

谐波点状峰结构及线状峰结构扩展区域估计采用区域扩张迭代算法进行.具体过程：（1）扩展区域标记，在迭代的每步开始，先从傅里叶幅值图中抽取出已确定的峰结构扩展区域；（2）曲面模拟，对抽取剩余的傅里叶幅值图用分块插值拟合法进行曲面估计，分块插值为块均值×（0.5×块方差）；（3）扩展区域增长，先计算傅里叶幅值图与拟合曲面之间的差异，然后计算该差异图像中每一频率点5×5局部标准差，如果已有扩展频率区域四周频率点的差异图像值大于相应的局部标准差，则标记为新的支撑域，同时原有傅里叶幅值图中该区域值由拟合曲面处相应值替代；（4）迭代终止，如果估计扩展区域邻近的平均局部标准差与其外界区域标准差相近，这时去除奇异谱峰结构区域后的傅里叶幅值图变得很光滑，则迭代终止.图6（a）和6（b）分别示出了图2（b）谐波点和短暂线支撑域的扩展过程.

上行为点状峰结构区域，下行为对应剩余傅里叶幅值图，从左至右迭代逐次增加

图6 谐波点及线区域支撑扩展示意图Fig.6 Estimation of harmonic peak and evanescent line support regions

2.4 织物起球纹理的非确定性成分提取

令点状及线状峰结构支撑域频率为Dυ，则纹理图像经离散傅里叶变换后分解的确定性成分为V（k，l）＝Y（k，l），（k，l）∈Dυ，相应非确定性谱成分W（k，l）＝Y（k，l），（k，l）∈D，（k，l）∉Dυ，确定性v（m，n）和非确定性w（m，n）分别由V（k，l）和W（k，l）的离散逆傅里叶变换所得.

图7和8分别为图2中含有周期性及方向性规则纹理图像的Wold分解结果图.

3 结果分析

图9为列举的几种典型织物Wold分解过程示意图.从左至右织物纹理分别为牙签条组织、简单色织物、印花及2种复杂色织物组织.从分解结果来看，除了印花组织中的低频纹理难以去除之外，其他织物纹理基本上能得到正确分解，同时还可看出分解的确定性纹理中不含毛球信息，说明非确定性纹理没有分解.

4 结 语

本文讨论了应用图像分析进行织物起球客观评估过程中的织物底纹纹理滤除问题，并对Wold纹理模型在织物起球纹理分解中应用的可行性进行了分析，提出包括谐波峰状点结构、线结构及其支撑区域扩展的Wold分解算法流程，特别是多尺度B-样条小波匹配滤波器在峰结构及线结构变换域中高斯奇异目标匹配检测应用，提高了 Wold纹理分解谐波区域检测的鲁棒性.通过典型起球织物规则及非规则纹理的分解结果得出，应用本文提出的 Wold纹理模型分解算法，能将含有毛球信息的非确定性纹理成分从织物底纹中分解出来，排除了周期性、方向性等确定性纹理成分的干扰，从而较好地解决了复杂织物底纹对毛球目标识别与分割的影响.

[1]徐增波.织物起球等级的计算机视觉评估[D].上海：东华大学纺织学院，2001.

[2]曹飞，汪军，陈霞.织物起球标准样照的图像分析[J].东华大学学报：自然科学版，2007，33（6）：751-755.

[3]周圆圆，潘如如，高卫东，等.基于标准样照与图像分析的织物起毛起球评等方法[J].纺织学报，2010，31（10）：29-33.

[4]ZENG Z，WANG L，WANG X.An integrated method of feature extraction and objective evaluation of fabric pilling[J].Journal of the Textile Institute，2011，102（1）：1-13.

[5]LIU X J，HAN H B，LU Y S，et al.The evaluation system of fabric pilling based on image processing technique[C]／／Proceedings of 2009International Conference on Image Analysis and Signal Processing.2009：44-47.

[6]ZHANG J M，WANG X G，PALMER S.Performance of an objective fabric pilling evaluation method[J].Textile Research Journal，2010，80（16）：1648-1657.

[7]XU Z B，LU K，HUANG X B.Evaluation of fabric pilling using light projection and image analysis techniques[J].Journal of Donghua University：English Edition，2000，17（4）：80-86.

[8]CHEN X，HUANG X B.Evaluating fabric pilling with lightprojected image analysis[J].Textile Research Journal，2004，74（11）：977-981.

[9]XU B G，YU W R，WANG R W.Stereovision for threedimensional measurements of fabric pilling[J].Textile Research Journal，2011，81（20）：2168-2179.

[10]FRANCOS J M，MEIRI A Z，PORAT B.A unified texture model based on a 2 -D wold like decomposition[J].IEEE Transactions on Signal Processing，1993，41（8）：2665-2678.

[11]LIU F，PICARD R W.Periodicity，directionality，and randomness：Wold features for image modeling and retrieval[J].IEEE Transactions on Pattern Recognition and Machine Intelligence，1996，18（7）：722-733.

[12]STOICA R，ZERUBIA J，FRANCOS J M. The twodimensional Wold decomposition for segmentation and indexing in image libraries[C]／／IEEE International Conference on Acousics，Speech and Signal Processing.1998：2977-2980.

[13]CHUN S L，PAU C C.Wold features for unsupervised texture segmentation [C]／／ International Conference on Pattern Recognition.1998：1689-1693.

[14]SIRAM R，FRANCOS J M，PEARLMAN W A.Texture coding using a Wold decomposition model[J].IEEE Transactions on Image Processing，1996，5（9）：1382-1386.

[15]BLANC R，COSTA J P，STITOU Y，et al.Assessment of texture stationarity using the asymptotic behavior of the empirical mean and variance[J].IEEE Transactions on Image Processing，2008，17（9）：1481-1490.

[16]YONG H，KAP L C.Texture decomposition by harmonics extraction from higher order statistics[J].IEEE Transactions on Image Processing，2004，13（1）：1-14.

[17]LOPEZ E，ALTAMIRANO R L.A method based on treestructured Markov random field and a texture energy function for classification of remote sensing images [C]／／ 5th International Conference on Electrical Engineering，Computing Science and Automatic Control.2008：540-544.

[18]FRANCOS J M，NARASIMHAN A，WOODS J W.Maximum likelihood parameter estimation of textures using a wolddecomposition based model[J].IEEE Transactions on Image Processing，1995，4（12）：1655-1666.

[19]WANG Y P，LEE S L.Scale-space derived from B-splines[J].IEEE Transactions on Pattern Recognition and Machine Intelligence，1998，20（10）：1040-1055.

[20]MALLAT S A. Theory for multiresolution signal decomposition： The wavelet representation [J]. IEEE Transactions on Pattern Recognition and Machine Intelligence，1989，11（7）：927-938.

[21]KENNETH R C.Digital image processing[M].New Jersey：Prentice Hall，1998.