缺少地面控制点的多源SAR影像联合定位方法
2012-09-15吴颖丹
吴颖丹,明 洋
(1湖北工业大学理学院,湖北 武汉430068;2中交第二公路勘察设计研究院有限公司,湖北 武汉430056)
合成孔径雷达(SAR)具有全天候、全天时的对地观测能力[1],卫星传感器技术的快速发展,使得获取同一地区不同SAR传感器影像越来越容易,利用多源SAR影像进行精确对地目标定位是一项关键技术.然而,就中低分辨率星载SAR影像而言,由于斑点噪声的影响,控制点的识别比较困难.在困难复杂地区,获取符合要求的地面控制点往往十分困难.因此,研究缺少地面控制点情况下的多源SAR影像联合定位是非常必要的.
对多源SAR影像联合定位而言,主要有如下两种方式:
其一是空间后方交会—前方交会的方法,如加拿大遥感中心Toutin利用ERS-1和SPOT全色影像进行了立体定位试验,获得30m的平面精度和20m的高程精度[2],邢帅等人尝试了将光学与SAR卫星遥感影像联立进行复合式定位,并对理论与方法进行深入研究和试验[3].为了提高定位精度,该方法需要利用地面控制点分别对每景影像定向参数进行精化,对控制点布设要求较高.
其二是区域网平差的方法,目前均采用SAR影像的严格成像几何模型建立误差方程,其理论严密、定位精度高.Lee采用改进的共线条件方程,对Landsat-7、KOMPSAT-1、SPOT-1、IKONOS 等 光学卫星影像进行了联合区域网平差,获得了平面2.76m,高程3.1m 的精度[4].Toutin对 Landsat-7ETM+、SPOT4HRV、ASTER VNIR、RADARSAT、ERS等影像,采用25个控制点进行平差试验,SAR影像可获得像元级的平面和高程精度[5].邢帅对多星多源 传感器 SPOT、IKONOS、ERS及其RADARSAT影像采用严格几何模型进行了联合区域网平差实验研究[6].
该类方法缺点在于:多源SAR影像成像几何模型的多样性,加大了程序实现的难度,并且定向参数间的强相关性也限制了所能获得的实际定位精度.近年来,相关学者研究了有理函数模型(RFM)拟合SAR严格成像几何模型的可行性,并获得可喜成果,但是利用RFM模型进行更深层次的几何处理鲜有文献报道.
有鉴于此,本文提出了一种基于RFM模型区域网平差的方法,以解决缺少地面控制点情况下的多源SAR遥感影像联合定位问题.将对我国某地区实际SAR影像资料进行联合定位试验,并与基于严格成像几何模型的方法进行比较,以验证该方法的有效性及其所能达到的对地目标定位精度.
1 星载SAR影像有理函数模型的建立
目前,星载SAR影像一般不提供RFM模型系数,即RPC参数,为此,本文采用与地形无关的方法解算RPC参数.即首先利用SAR影像的严格成像几何模型生成基于不同高程面的密集、分布均匀的虚拟控制格网,然后利用虚拟控制点按最小二乘原理解算得到RPC参数.其计算流程如图1所示.

图1 星载SAR影像RPC参数计算流程图
对RPC参数计算而言,与光学遥感影像的不同主要在于建立控制格网和检查格网所采用的成像模型.
这里采用SAR影像广泛使用的距离多普勒数学模型,不同类型的传感器,可以根据对应的星历参数文件建立.对于解算中参数的强相关问题,可通过岭估计或者谱修正迭代法加以克服.
2 基于RFM模型的多源SAR影像区域网平差
按照前面所述方法计算得到的RFM模型,只是对SAR影像严格成像几何模型的精确拟合.而SAR影像头文件提供的星历参数,如卫星的位置、速度等信息,不可避免地存在测量误差,为消除此类误差,一般通过在像方定义仿射变换模型来改正[7],即:
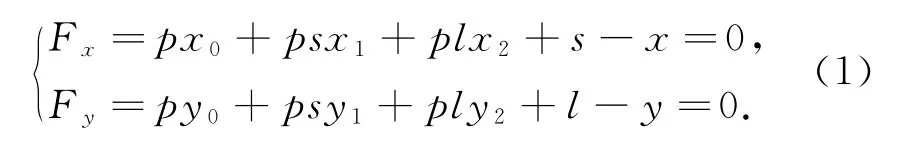
式中,(x,y)为地面控制点在影像上量测坐标的列号和行号,(s,l)为地面控制点利用RPC参数投影到影像上的坐标列号和行号,(pxi,pyi)(i=0,1,2)是仿射变换系数.
对于每个连接点和地面控制点,以其所在像片的仿射变换系数和对应的物方坐标为未知数,对式(1)线性化,可得到误差方程:

(dlat,dlon,dheight)为连接点或地面控制点的物方坐标.式(2)可以记为:

对于地面控制点坐标,将其视为带权观测值进行处理,还需列立如下误差方程:
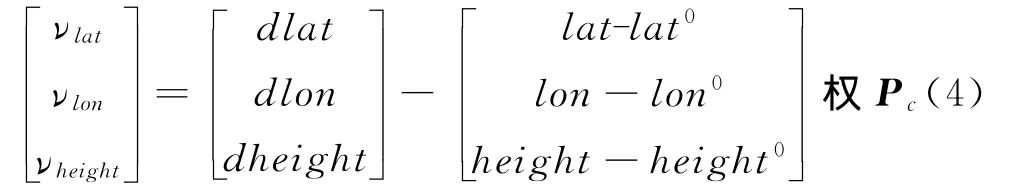
其矩阵形式为:

综合式(3)与式(5),即为基于RFM模型的区域网平差模型.
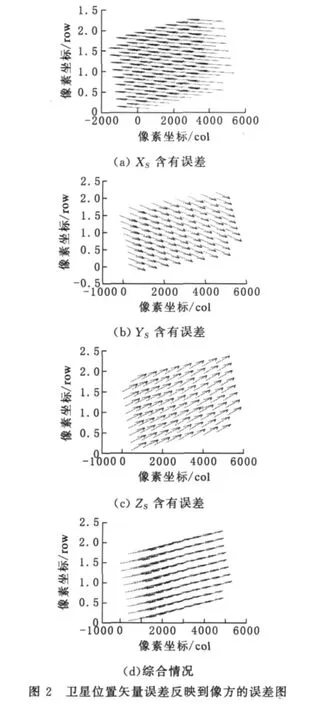
为了对像方仿射变换误差改正模型的有效性进行分析,本文选取了一景ENVISAT ASAR部分系统参数进行了仿真实验.具体步骤如下:1)在给定的区域范围内,均匀选取若干点位,借助全球免费DEM数据,获取其大地坐标;2)对均匀分布点的大地坐标,利用严格几何模型进行间接定位计算对应的像点坐标,这样可以得到一套精确的检查点坐标;3)对精确的定向参数引入系统误差,得到含误差的定向参数;4)最后分析定位结果在像平面的误差特性.第一组实验分别在XS、YS、ZS三个方向引入100m的误差,并考虑其综合作用的影响;第二组实验分别在VSX、VSY、VSZ三个方向引入50m/s的误差,同样考虑其综合作用的影响.图2、图3分别给出了位置、速度矢量误差引起的对地目标定位误差反映在像方的误差图.
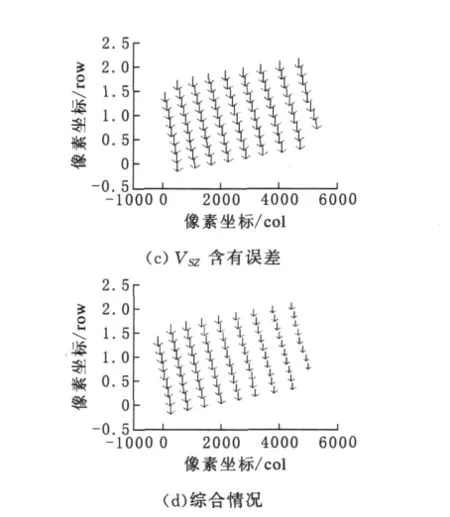
图3 卫星速度矢量误差反映到像方的误差图
从图中可以看出,平台位置误差主要引起像点列方向的系统偏移,平台速度误差主要引起像点行方向上的系统偏移.对于中低分辨率影像而言,如ENVISAT ASAR影像,定向参数误差引起的定位误差在像方仍然表现出比较明显的系统性,利用仿射变换模型可以消除大部分的系统误差.

3 实验及其结果分析
为了验证本文方法的有效性,这里选取了我国四川地区的一景ENVISAT影像和一景Radarsat-1影像进行了多源SAR遥感影像联合定位试验.地面控制点的平面坐标从1∶10 000比例尺的数字正射影像图上读取,高程值从1∶10 000比例尺数字高程模型中通过平面坐标内插得到.影像间的连接点则通过匹配算法和人工量测的方式得到.试验影像的主要参数如表1所示.
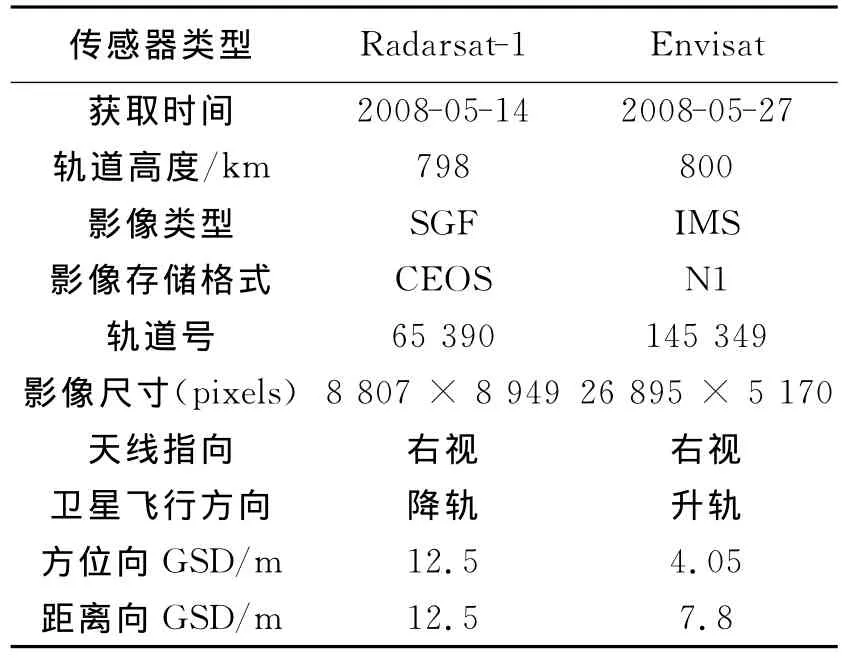
表1 实验影像主要参数
首先,本文采用前面所述方法计算两景影像对应的RPC参数,这里选取控制点格网大小为30×30,检测点的格网大小为60×60,高程分层数设为6,采用分母不相同的三阶RFM模型进行拟合.以ENVISAT影像为例,其平面最大误差为0.0004像素,平面精度为0.00002像素.结果表明,所计算得到的RPC参数可以精确拟合单景SAR严格几何模型.
为了分析基于RFM模型区域网平差的多源SAR影像联合定位结果,本文不仅对不同的地面控制点布设方案下的定位结果进行了比较分析,而且对基于严格几何模型的区域网平差进行了对比分析.其中,周边稀疏布点方案的影像控制点和检查点的布设情况如图4所示,△表示控制点,○表示检查点.表2列出了联合定位平差结果.

表2 两种平差模型不同布点方案的精度比较m

图4 控制点和检查点分布示意图
通过分析表中的数据,可以得出如下结论:
1)基于RFM模型的平差方法受地面控制点影响较小.在仅利用一个地面控制点情况下,基于RFM模型的方法定位精度为平面43.731m,高程22.871m,比较接近于周边稀疏布点时的定位结果.
2)当地面控制点数目较少、分布不太好时,如周边稀疏布点情况,基于RFM模型平差方法可以取得优于基于严格几何模型平差方法的定位精度,其非常适用于缺少地面控制点情况下多源SAR影像联合定位.而基于严格几何模型的平差方法,由于需要解算的定向参数较多、能利用的地面控制点过少,从而解算精度不高甚至无法求解.
3)增加控制点的数量,不能显著提高RFM模型区域网平差的定位精度,而在控制点布设条件良好情况下,基于严格成像几何模型区域网平差方法将优于基于RFM模型区域网平差方法,尤其是高程方向上.因此,研究更合适的误差改正模型是下一步的研究方向.
4 结束语
针对缺少地面控制点情况下的多源SAR遥感影像的联合定位问题,提出了一种基于RFM模型区域网平差的方法.通过我国四川地区实际影像资料的试验研究表明,基于RFM模型的多源SAR影像区域网平差,受地面控制点数目和分布状况影响较小,当地面控制点数量偏少、分布不好时,能获得较稳定且良好的平差方法,可作为多源SAR影像联合定位的一种有益补充方案.所采用的像方仿射变换模型,可以改正大部分的系统误差,研究更合适的SAR影像误差改正模型是下一步研究的重点.
[1]肖国超,朱彩英.雷达摄影测量[M].北京:地震出版社,2001.
[2]Toutin T.Stereo-mapping with SPOT-5and ERS-1 SAR Images [J].International Journal of Remote Sensing,2000,66(8):1 657-1 674.
[3]邢 帅,徐 青,靳国旺,等.光学与SAR卫星遥感影像复合式“立体”定位技术的研究[J].测绘学报,2008,37(2):172-177.
[4]Lee Y.A study on aerial triangulation from multi-sensor imagery[J].Koreon Journal of Remote Sensing,,2003,19(3):255-261.
[5]Toutin T.Spationtriangulation with multisensor hr stereo images[J].IEEE Transactions on Geoscience and Remote Sensing,2006,44(2):456-462.
[6]邢 帅,徐 青,刘 军,等.多源卫星遥感影像的光束法区域网平差[J].测绘学报,2009,38(2):125-130.
[7]Grodecki J,到 Dial G.Block adjustment of high-resolution images described by rational functions[J].Photogrammetric Engineering & Remote Sensing,2003,69(1):59-69.
