双层圆柱壳体水下振动噪声结构传递路径分析
2012-09-15曹跃云杨自春何元安
张 磊,曹跃云,杨自春,何元安
(1.海军工程大学 船舶与动力学院,武汉 430033;2.中国船舶工业集团公司 船舶系统工程部,北京 100036)
有限长双层圆柱壳体结构是潜艇等各种航行器舱段的典型结构形式。这些航行器的结构噪声来源于内部机械激励壳体振动,并带动周围流体介质振动产生声辐射,它严重影响了水下航行器的整体声学性能[1]。为了提高水下航行器的声学性能,进行主要噪声源和噪声传播途径的识别、量化,针对性地控制结构振动与噪声的传递是极其必要的工作。
结构振-声传递路径分析(Transfer Path Analysis TPA)是辨识主要激励源和相应传递路径的重要方法,该方法是一种基于试验的振动噪声分析方法,通过TPA可以确定各路径传递的激励能量在总能量中的贡献,从传递路径的角度找出对辐射噪声起主导作用的环节,通过控制这些环节,如使振源强度,路径声学灵敏度等参数在合理的范围内,以使水下声辐射控制在预定目标值内[2]。TPA方法在国内外的汽车设计领域已有较为成熟的应用[3-4],然而水下结构的振 - 声TPA的报道却非常少见,特别对于水下双层加肋圆柱壳体模型。由于该类水下结构具有较强的流固耦合特性,振-声传递特性十分复杂,试验难度大,使得水下结构TPA实施难度加剧。本文针对水下双层圆柱壳体的特点建立了振-声TPA模型,结合典型激励下双层圆柱壳体舱段模型的水下振动-声辐射试验,实现噪声源和噪声传递路径的识别、量化,进而指导结构的声学优化、预报和采取针对性的减振降噪措施,具有重要的工程意义。
1 传递路径分析的基本原理
1.1 传递路径分析方法
结构振-声传递路径为机械设备产生振动激励,通过基座的衰减或放大作用,传递到艇体联节点上并表现为力激励,此力再通过艇体传递到各处使得壳体振动从而辐射出噪声。对于某一激励源,如果已知某一路径上的传递函数和工作载荷,该路径对目标位置噪声的贡献量可表示为:

式中,Hi'(f)是传递函数,Fi(f)为激励力的频谱。Pi,stru(f)为目标点响应,可以是声压或加速度等,此处选择声压。如果有n条路径,总响应可以是各路径分量的线性叠加:
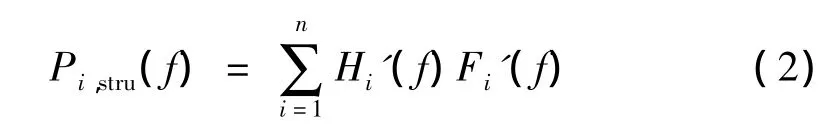
传递路径分析(TPA)必须先获得结构噪声各传递路径的传递函数及其工作载荷,工作力的获取方法主要有:直接测量法,复刚度法,矩阵求逆法和驱动点频响函数法等[2],其中后三个为间接法。而获取传递函数的方法主要有直接测量法和基于互易性原理的测量方法[3],本文采用逆矩阵法来求解激励载荷,传递函数为频率响应函数,由直接测量法获得。
对于一线性时不变系统,当有激励 F1,F2,…,Fn时,存在响应 X1,X2,…,Xm,由系统的运动方程可得:
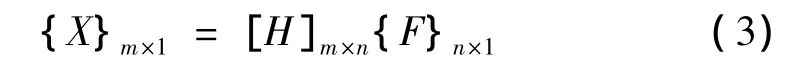
在确定了频响函数矩阵及响应向量的傅氏谱后,便可计算载荷谱。但实际上,常常是欲识别的载荷数与响应测点数不相等,即[H]m×n的逆矩阵不存在,这时可由矩阵理论中的广义逆矩阵法得到载荷识别的公式:

式中,[H]m×n为载荷计算的频响函数矩阵其共轭转置矩阵,元素Hij=Xi/Fj为Xi响应到输入Fj的频响函数;{F}n×1为路径载荷力列向量;{X}m×1为参考点响应信号列向量。
为了准确获得工作力的估计,应合理布置壳内参考测点的数目和位置,而且需要方程(3)中满足m>n,通常取m≥2n[2]。由于结构的模态特性,参考点的响应之间存在较强相关性,使得载荷计算的频响函数矩阵[H]m×n中包含的结构信息存在很大的相似性,这将导致频响函数矩阵的病态。对频响函数矩阵求逆会出现不稳定,又由于观测噪声不可避免,将导致工作载荷与其准确值差异很大,结果不可信。正则化方法是求解此类不适定性问题的有力工具,最著名的为Tikhonov正则化方法[5]。当频响函数矩阵病态时,将式(4)进行Tikhonov正则化可得到:

式中:HT为频响函数矩阵的共轭转置;L为正则化矩阵,本文取为单位矩阵;λ为正则化参数,其选择是求解不适定问题的关键,Hansen[6]针对不适定问题提出的L-曲线法是一种较好的方法,当λ∈(0,∞)且离散Picard条件成立时,曲线形状像字母“L”,L曲线角点处的曲率最大,选择其对应的λ即为所求的正则化参数。
1.2 频响函数估计
激励力到参考点加速度响应的频响函数矩阵H及激励力到壳外目标点声压响应的频响函数矩阵H'的确定是TPA的核心,直接影响到TPA结果的准确性。由于在试验测试过程中不可避免地存在干扰误差,因此频响函数估计精度问题是工程技术人员必须面对的问题之一。系统频响函数估计的误差主要有输入输出测量误差(如加性随机噪声干扰)和信号处理误差(如频率泄露误差)等。工程上减少加性随机噪声干扰影响常用的频响函数估计方法有估计和估计,前者主要考虑响应被污染的情况,后者则考虑了激励信号被污染的情况,两者都是有偏估计。在一般实际测量中,输入输出加性噪声是同时存在的。为此,本文引入能同时考虑输入输出噪声的估计模型来识别频响函数,是在总体最小二乘观点上求得的,其估计公式为[7]:

式中,SXi,Xi(f)为响应信号的自谱;SFj,Fj(f)为激励力的自谱;SFjSFjXi(f)为激励信号与响应信号的互谱。
在系统频响函数估计中,时域截断引起的频谱泄露也是影响频响函数估计精度的主要原因之一,本文将通过选择恰当的窗函数和相邻数据块重迭比例来减小泄露误差。为了进一步提高频响函数的估计精度,对频响函数估计采用多次平均。
2 双层圆柱壳体水下振动-声辐射试验
为了研究双层加肋圆柱壳体在水下的振-声传递特性,本文进行了某双层加肋圆柱壳体模型的水下振动-声辐射试验,试验模型如图1。在内壳体上选择三个激励源,位置分布如图2所示,试验只考虑垂向激励的响应。在内壳体上布置振动加速度计共29个,振动加速度计的布置位置对模型振-声传递路径分析有很大的影响,此处在各激励点附近布置4个加速度计,这些部位的响应包含工作载荷的信息较丰富,其他加速度计布置遵循同方向的测点不要布置太近以及尽量不要将加速度计布置在反映激励点作用效应雷同的部位等原则。在壳体外布放5枚水听器,加速度计和水听器布放位置与编号见图3。

图1 双层圆柱壳体模型Fig.1 The cylindrical double-shell model

图2 激励源布放位置Fig.2 The location of excitation source
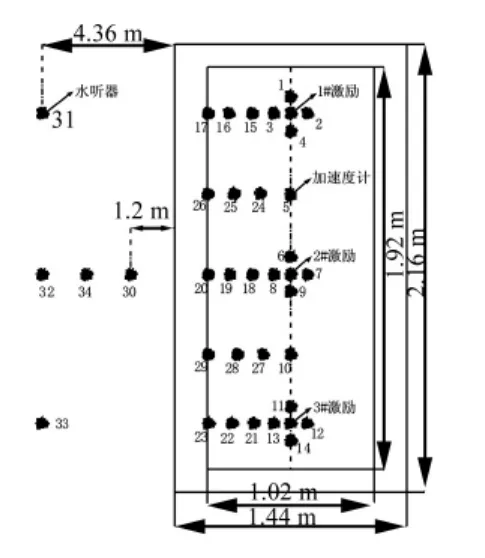
图3 传感器布置示意图Fig.3 The location of the sensor
试验在北京某消声水池内进行,模型吃水3.75 m,水听器布放深度均为4 m。主要测量设备有:PFI28000信号调理器;NI1042q机箱+4498板卡的数据采集器;ACP-4320工控机;复合棒激振器;安捷伦33220信号源;BK2692电荷放大器;L6和JYH1000A功放;RHSA-20水听器;PCB加速度计。试验中壳外的辐射噪声与壳体的结构振动数据实现了同时基采集,获得的数据不仅可以分析其自功率谱,还可进行涉及它们之间相互关系的互谱分析以及其他的综合处理。采样频率为16 384 Hz,采样时间10 s,加速度、声压的参考值分别为 10-6m/s2与10-6Pa。
首先进行单源激励试验,同时测得水下双层圆柱壳体内的振动加速度信号和壳外的声压信号,并利用1.2节中的)Hv估计对激励力到参考点加速度响应的传递函数H及激励力到壳外目标点声压响应的传递函数H'进行估计。在进行频响函数估计时,在每个激励点分别单独进行激励,采用多次激励,用平均的方法(作了6次平均)来获取频响函数以进一步减少噪声信号的影响。同时选取 kaiser窗函数[8],该窗函数全面反映了主瓣和旁瓣衰减之间的交换关系,它定义了一组可调的由零阶贝塞尔Bessel函数构成的窗函数,通过调整参数β可以在主瓣和旁瓣衰减之间自由选择它们的比重,此处取窗长度N=9 182,参数β=2,相邻数据块重迭比例取为1/2。最后进行3个激励源同时激励下的试验,此处选一种信噪比较高的工况进行分析,具体为:1#激振器发射连续宽频信号sinc,频率取为500 Hz,2#激振器发射连续宽频信号sinc,频率取为1 000 Hz,3#激振器发射连续正弦信号,频率取为3 000 Hz,功率输出均为92 vpp。对应的3个激励源分别单独开启,利用分布运转法来进一步验证振-声传递路径的分析结果。
3 试验数据处理与分析
3.1 病态频响函数矩阵的诊断与正则化
为了准确求得工作载荷,本文将参考点选为m=2n,模型共有3个路径点即参考点数为6个,且需要选取恰当的参考点组成较为良态的频响函数矩阵。为了避免构造出病态的矩阵,需首先引入病态矩阵有效的诊断方法。矩阵的条件数是诊断矩阵是否病态的有效方法,根据矩阵条件数的定义,将其推广到长方体矩阵有:

其中,σ1是频响函数矩阵H的最大奇异值,σr是H的最小奇异值。由于每一个频率处的频响函数矩阵都对应着一个condition值,此处根据condition曲线对载荷计算矩阵的病态程度进行判断。当condition曲线在整个频率范围内都较小时,表示构造的矩阵质量较好,得出的计算结果比较好。图4 给出了最佳参考点(1,5,7,11,12,14)构造的频响函数矩阵的condition(f)曲线,将condition(f)>100对应的矩阵定义为病态矩阵[9]。尽管图4的条件数总体较小,但在个别频率点处的条件数仍然较大,则相应的频响函数矩阵是病态的。利用1.1节的正则化方法对病态矩阵进行修正,通过分析可知共有20个频点对应的频响函数矩阵为病态。此处以条件数大于200时的频响函数矩阵为例,频点为(500 Hz,3 008 Hz,6 499 Hz,7 499 Hz),由 L曲线法求得对应的正则化参数为(0.003 4,2.335 9,1.590 1,6.261 1)。
3.2 壳外噪声合成与验证
本文在不同激励幅值下求得激励点到目标点的传递函数,结果表明传递函数基本不随激励幅值和激励先后顺序的变化而变化,可认为圆柱壳体结构满足线性的不变性。求得所有频响函数和工作载荷后,结合所选工况作用下测得的参考点加速度信号和目标声压信号,通过MATLAB编制TPA程序对三个激励源到壳外目标点声压贡献量进行合成,并与实测结果相比较,见图5(考虑到水池消声频率下限的限制和试验场工频干扰等不利因素,分析频段从200 Hz开始)。比较图5中壳外目标点的合成声和实测噪声发现,合成的频谱频域分布与实测结构基本一致,主要的峰值频率均能一一对应,其频率处的幅值与实测噪声幅值吻合很好,除了个别异常波动的点,其余相差均在3 dB左右,满足水下噪声源识别的基本要求。并与用Hij=Xi/Fj进行频响函数估计即传统TPA合成结果进行比较,从目标点噪声的1/3倍频谱图比较(图6、图7)可以看出,30#水听器主要峰值频率处的声压级均大于32#水听器,即满足辐射噪声随测量距离的增加而衰减。本文基于)Hv估计建立的TPA模型应用了互谱技术和平均技术减少输入输出加性随机噪声的干扰,并且通过加窗等方法减少了频率泄露的影响,得到的结果要大大优于传统TPA。这些都验证了建立的水下双层圆柱壳体振-声TPA模型及试验的正确性。
误差产生的主要原因可能有:
(1)试验中只考虑了激励点垂向的振-声传递路径,忽略了轴向和周向的传递路径,从而产生了误差。
(2)系统中存在的非线性失真,不确定边界等问题造成的频响函数估计误差。单源激励由于工况不多变不能激起详细的频率信息,多次激励平均次数不够多等也是造成频响函数估计误差的原因。
(3)参考点之间的振动响应的相关性造成工作载荷估计误差。
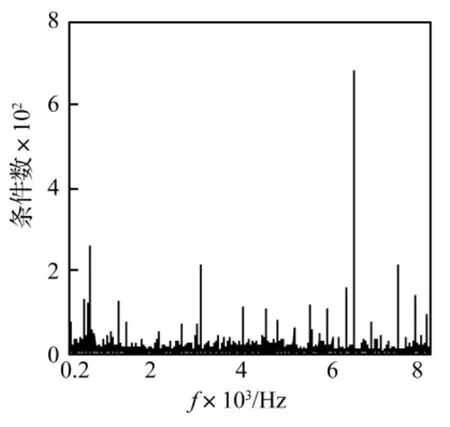
图4 条件数变化曲线Fig.4 The curve of condition number
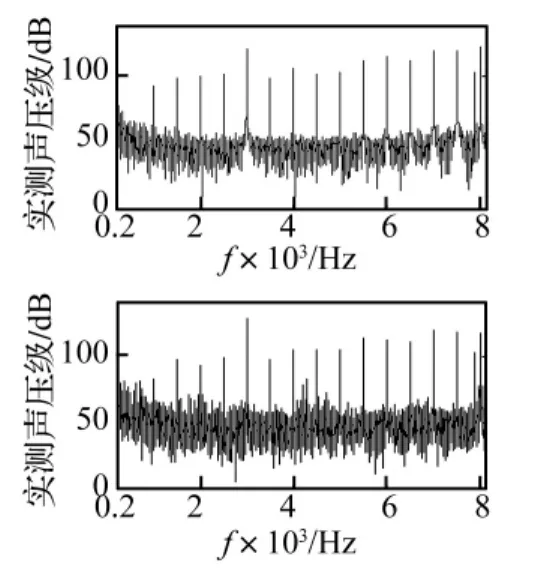
图5 32#目标点实测值与合成值比较Fig.5 Contrast of synthesized noise and compute result at 32#

图6 30#目标点实测值与合成值1/3倍频谱图比较Fig.6 Contrast of 1/3 octave spectrum at 30#

图7 32#目标点实测值与合成值1/3倍频谱图比较Fig.7 Contrast of 1/3 octave spectrum at 32#

图8 1#激励传递路径贡献比较图Fig.8 Comparison of contribution of transfer path 1#

图9 2#激励传递路径贡献比较图Fig.9 Comparison of contribution of transfer path 2#
3.3 壳外噪声贡献量分析
图8 和图9为1#和2#振源单独激励时32#目标点的响应与TPA计算得到的1#和2#传递路径的贡献比较图。可以看出,两者的变化趋势相同,在主要峰值频率处TPA得到的路径贡献量与分布运转得到的结果基本一致。以主要峰值频率处的贡献和为基本量,通过TPA得到3个振源在目标点30#和32#的贡献排序均为1#>2#>3#,与分布运转法得到的结果一致,进一步说明了本文建立的TPA模型具有相当的可靠性。
图10和图11为各路径对壳外30#和32#目标点的噪声贡献谱图,可以看出,2个目标点的噪声在频率3 kHz、4 kHz、4.5 kHz左右均有峰值。在 3 kHz 左右 3个振源对30#目标点贡献量排序为2#>1#>3#,对32#目标点的贡献量排序为2#>3#>1#,30#、32#目标点在4.5 kHz时振源的贡献量排序均为1#>3#>2#。即频率相同时各振源在不同目标点的贡献可能不同,而相同目标点处各振源在不同频率下贡献量也可能不同,这些都可以通过TPA方法进行定性和定量的分析。可见,TPA可以有效地实现振源的贡献量排序。

图10 30#目标点各传递路径噪声贡献谱图Fig.10 Contribution of each transfer path at 30#

图11 32#目标点各传递路径噪声贡献谱图Fig.11 Contribution of each transfer path at 32#

图12 对数坐标中频响函数与工作力对比分析图Fig.12 Comparison of FRF and excitation force in logarithmic coordinate
3.4 频响函数与工作力分析
通过对双层圆柱壳外噪声贡献量分析以后,可以对壳外噪声主要贡献量的路径进行频响函数与工作力的分析,由此可以判断是壳体结构的问题还是噪声源的问题。图12为1#振源到32#目标点主要峰值频率处的频响函数与1#振源工作载荷的对数图,结合图8可知,频响函数在1 kHz~2 kHz之间出现了3处峰值,而工作力均未出现峰值,但图8中对应频率处却出现了峰值,说明壳体结构起到了主要的传递作用。在3 kHz左右频响函数峰值较小,图8中对应频率处的峰值反而较大,这是由于工作力出现了较大峰值,导致最终响应出现较大峰值。识别出了影响壳外噪声的是壳体结构的问题还是噪声源的问题,便可以针对性地控制结构振动与噪声的传递。
4 结论
(1)阐述了TPA的基本概念及试验方法和步骤,建立了水下双层圆柱壳体的振-声TPA模型。模型中用)Hv估计求得频响函数,通过互谱技术和平均技术减少了输入输出随机噪声的干扰,并且通过加kaiser窗减少了频率泄露的影响。在逆矩阵法求解耦合激励力时,选取了参考点数m=6且condition曲线为最佳时的组合,从而构造出较为良态的频响函数矩阵,出现的病态矩阵用Tikhonov正则化方法进行了修正。
(2)利用matlab软件编制TPA程序,在噪声与结构振动数据同时基采集的基础上,计算得到合成的频谱频域分布与实测结构基本一致,并且分析了误差产生的主要原因。以32#目标点为例,进行了各条路径总的贡献量排序并与分布运转的结果相比较,两种结果一致,证明TPA可以有效地实现振源的贡献量排序。利用频谱贡献云图以及频响函数与工作力的对比分析,得到各条结构传递路径对壳外噪声的贡献并且识别出了影响壳外噪声的是壳体结构的问题还是噪声源的问题。可见,本文建立的TPA模型能有效地进行水下双层圆柱壳体结构噪声源的识别、量化和噪声传播途径的识别,同样可以指导进行水下噪声实时预报和采取针对性的减振降噪措施。
[1]何元安,杨德森.水下结构辐射噪声估算方法实验研究[J].船舶力学,1999,3(2):58 -62.
[2]Knapen P L.Transfer path analysis related to booming,performed on a car[D].The Netherlands:Eindhoven University of Technology,2006.
[3]Kim S J,Lee S K.Prediction of interior noise by excitation force of the powertrain based on hybrid transfer path analysis[J]. InternationalJournal ofAutomotive Technology,2008(9):577-583.
[4]王万英,靳晓雄,彭 为,等.轮胎振动噪声结构传递路径分析[J].振动与冲击,2010,29(6):88-92.
[5]Choi1 H G,Thite A N,Thompson D J.Comparison of methods for parameter selection in Tikhonov regularization with application to inverse force determination[J].Journal of Sound and Vibration,2007(304):894-917.
[6]Iain J D.On the inversion of diffusion NMR data:Tikhonov regularization and optimal choice of the regularization parameter[J].Journal of Magnetic Resonance,2011(211):178-185.
[7]White P R,Tan M H,Hammond J K.Analysis of the maximum likelihood,total leastsquares and principal component approaches for frequency response function estimation[J].Journal of Sound and Vibration,2006(290):676-689.
[8]Datar A.Jain A.Sharma P C.Design of Kaiser window based optimized prototype filter for cosine modulated filter banks[J].Signal Processing,2010,90(5):1742 -1749.
[9]张永军,吴 磊,林立文,等.摄影测量中病态问题的条件数指标分析[J].武汉大学学报(信息科学版),2010,35(3):308-312.
