基于GIS、Delaunay三角形的复杂地形区经济重心获取新方法

郭 兵，陶和平，刘斌涛，姜 琳

（1.中国科学院·水利部成都山地灾害与环境研究所，四川成都610041；2.中国科学院研究生院，北京100049；3.成都信息工程学院，四川成都610225）

基于GIS、Delaunay三角形的复杂地形区经济重心获取新方法

郭 兵1，2，陶和平1，刘斌涛1，姜 琳3

（1.中国科学院·水利部成都山地灾害与环境研究所，四川成都610041；2.中国科学院研究生院，北京100049；3.成都信息工程学院，四川成都610225）

传统的经济重心求算方法中忽略了经济发展的辐射效应及城市化过程产生的聚集效应和邻近效应，特别是地形对经济发展的影响。该文提出了基于GIS和Delaunay三角形的新的研究方法，通过空间插值Cokriging算法以及对空间点集的平面剖分并结合GIS进行多重迭代运算，在一定程度上解决了传统算法中存在的不足。以2005年四川省各县市的国民生产总值为例，简要阐述了研究方法的技术流程，为以后人口重心、耕地重心等其他社会评价指标重心的研究提供了新方法。

经济重心；Delaunay三角形；空间插值；Kriging

0 引言

经济重心是指区域经济空间中的某一点，在该点各个方向上的经济力量能够维持均衡；它类似国民生产总值、物价指数，可作为宏观分析的经济指标之一，研究国家或区域发展的方向、平衡等问题，以及用来评估空间发展政策的效果［1］。美国从1970s就开始了对空间上多种社会、经济和自然资源重心问题的研究。我国起步较晚，樊杰等［2］用重心方法率先研究了改革开放以来我国农村工业重心的变动；李义俊［3］研究了我国的人口重心及其移动轨迹（1912－1978年），揭示了我国现代人口的变化概况；包玉海等［4］对内蒙古耕地重心的驱动因子做了分析，认为其包括社会历史、自然、政策及经济利益驱动。此外，周民良［5］分析了我国经济重心、区域差距之间的关系；徐建华等［6］对人口重心与经济重心的演变进行了对比分析；陈希华［7］对山东省产业重心转移与可持续发展进行了研究；乔家君等［8］分析了近50年来中国经济重心移动路径。总体看，经济重心的研究主要体现在两方面：一是通过GIS将常规经济重心公式计算的结果以地图的形式展示出来，其中GIS只起到可视化的效果；二是通过对多年经济重心的经纬度迁移及其移动轨迹的角度变化的对比分析得出最终结论。

目前，关于经济重心的研究多在传统的获取经济中心的算法基础上对于某个省或全国进行纵向时间序列的叠置分析，而对于经济重心的获取方法上没有很大改进，从而造成研究中重心迁移轨迹产生较大的误差，进而对最终研究成果的精确度产生很大影响。本研究提出基于GIS和Delaunay三角形的新方法，改进了传统的经济重心计算中存在的不足。

1 传统的经济重心算法及其不足

重心的概念起源于力学，是指在区域空间上存在某一点，在该点前后左右各个方向上的力量对比保持均衡。在物理学中其计算公式［1，8］如下：

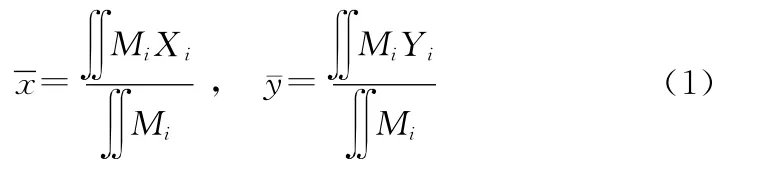
其中：（xi，yi）为i处的地理坐标，因此上式可改为：

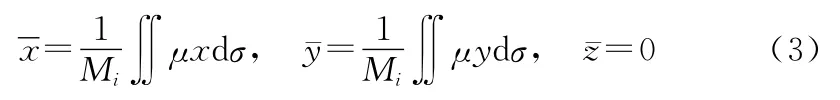
在经济研究中，对一个拥有若干个次一级别的行政单元的国家或省而言，计算其经济重心通常是借助各次级行政区的经济属性和地理坐标来表达。若某一个区域由n个次一级别的行政单元构成，第i个次区域的行政中心的地理坐标是（xi，yi），Mi为第i次区域的经济量值，则该区域的经济重心的地理坐标表示为：

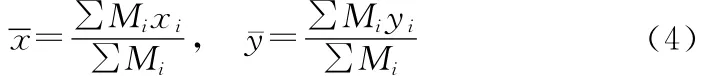
由以上公式可以看出，经济重心的数值由经济指标的大小及其地理坐标共同决定。

鉴于近几十年来中国城市化发展突飞猛进，造成了区域经济发展过程的相互影响、相互制衡［2，4］。传统的经济中心求算过程是将所获取的中心城市的经济指标进行整体一次性求算，所以造成了以下不足：1）没有考虑到经济发展的区域不均衡性及其各地区间的内在联系，研究经济发展规律时只考虑时间效应，而不考虑空间的相互作用是片面的。2）传统的计算公式是一次性综合计算，所以次级行政单元较少且分布不均匀时计算结果往往产生很大的偏差。3）没有充分考虑到经济发展的辐射效应，特别是大城市对周边地区的带动作用。4）仅利用了GIS的可视化功能，而没有充分利用GIS的分析及数据处理功能，未充分发挥GIS的优势。5）传统的经济重心计算公式适用于小范围区域的研究，当研究区域特别大（如计算全国经济重心）时，计算结果的误差会很大。6）在研究地形复杂的西部山区时，不考虑地形因子对经济发展的影响，往往会产生很大的误差。

2 本研究方法的基本原理及流程

2.1 空间插值

空间数据的插值即对一组已知空间数据（可以是离散点的形式，也可以是分区数据的形式），要从这些数据中找到一个函数关系式，使该关系式最好地逼近已知的空间数据，并能根据该函数关系式推求出区域范围内其它任意点或任意分区的值［9］。空间位置上越靠近的点，越可能具有相似的特征值；而距离越远的点，其特征值相似的可能性越小。这是空间插值技术最基本的理论假设，这一基本理论恰好符合经济的辐射效应和近邻效应。

本研究采用Kriging插值法，即利用区域化变量的原始数据和变异函数的结构特点，对未采样点的区域化变量的值进行最优、线性、无偏估计。这种方法是在分析已测样点的形状、大小、空间位置相互关系，已测样点与待估样点的相互空间关系以及变异函数提供的结构信息的基础上，对待估点进行的一种无偏最优估计。它最大限度地利用了空间取样所提供的各种信息，不仅考虑了该样点的数据，还考虑了邻近样点的数据，不仅考虑了待估样点与邻近已知样点的空间位置，而且考虑了各邻近样点彼此间的位置关系，同时利用了已有观测值空间分布的结构特征，从而使这种插值方法比其它方法更精确，并且能够给出估计误差。设在某一区域内采样点位置处的观测值为z（xi），i＝1，2，3，…，n，则预测点x0的估计值xi可以通过周围n个采样点的观测值z（xi）的线性组合来求取，即：

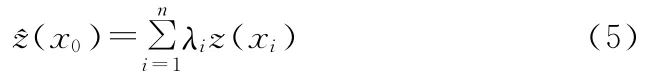
式中：λi为采样点xi的权重。与距离反比插值法的权重不同的是，此处xi为所赋的权重值不仅考虑了预测点与采样点之间的距离，而且考虑了预测点与采样点之间、采样点彼此之间空间分布关系。

要得到无偏最优估计值，须满足两个条件：第一，无偏估计，即E［＾z（x）－z（x）］＝0；第二，估计方差最小，Var［＾z（x）－z（x）］→min。

则要求权重λi满足下列方程：

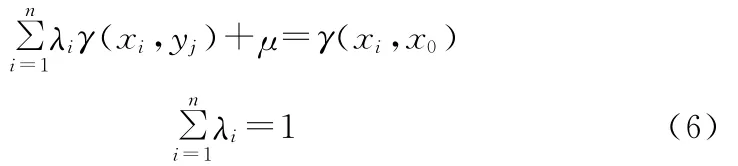
式中：γ（xi，yj）为采样点xi与yj间的半变异值，γ（xi，x0）是采样点xi与内插点x0间的半变异值，μ是与方差最小化有关的拉格朗日乘数。由此方程计算出权重λi的值，即可求出待估点x0处的内插值＾z（x0）。

Kriging方法的估值是根据已有资料加权线性结合而获得，是无偏的（Unbiased），此方法使平均残差或误差接近于0是最好的。

2.2 Delaunay三角形

Delaunay三角剖分具有最小内角及平均形态比最大的性质，因此它是给定区域的点集的最佳三角剖分［10］。Delaunay三角剖分能够尽可能地避免病态三角形的出现，使获得的所有三角形的最小内角之和最大。构建Delaunay三角网就是一个与其最近两个相邻点连接以尽可能形成等角三角形的反复过程。

本文采用横向扩张算法进行Delaunay三角剖分［11－13］，其具体步骤为：1）先将待构网的离散点集按横坐标（或纵坐标）升序排列，这时各点在点集中的顺序即是空间上从左到右排列（图1a）。2）由最左侧的3个点连成三角形，并确保它的顶点为逆时针排列，这个三角形实际上构成了这3个点的初始凸包（图1b）。3）将凸包边（为有向边，其指向与三角形顶点的排列顺序一致）存储在一个集合中。4）取出点集中的下一个点P，遍历凸包边集合，找出符合条件的边，这里的条件为P位于边的右侧（图1c～图1g）。5）将第4步找出的所有边与点P构成新三角形，从凸包边集合中删去这些边，因为它们已不再是凸包边界上的边。每条边的两顶点与P的连线形成了两条新边，通过判断边集合中是否有新边的反向边即可知新边是否为凸包边。若有，则新边即为非凸包边（图10），这时不仅新边不加入集合，还要从集合中删去其反向边；如果是凸包边则加入到凸包边集合中。6）重复步骤4、5，直至点集为空。7）用LOP法则优化所有三角形（图1h）。另外，在第5步及第7步都要处理好三角形之间的邻接关系。

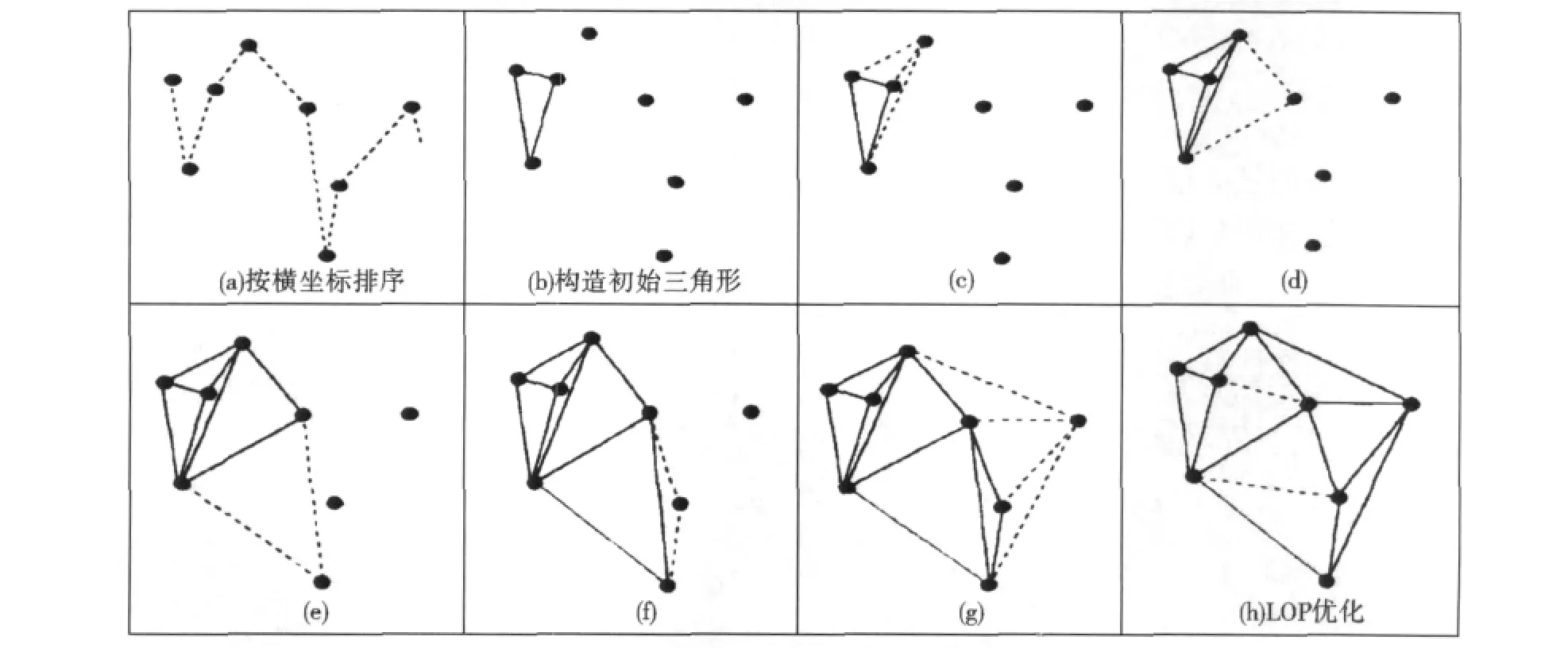
图1 横向扩张法的构网过程Fig.1 Process of generating triangulation by horizontal expanding method

2.3 研究流程

研究流程包括：1）将获取的各次级行政单元中心的经济指标所形成的点数据利用ArcGIS进行反距离加权法插值，获取研究区域的经济指标栅格图。2）以研究区域的各次级行政区划中心（经纬度坐标）为点集，进行Delaunay三角形剖分。3）利用传统经济重心计算公式计算每个Delaunay三角形的重心。4）将第3步获取的重心点数据（经纬度坐标）以及第1步获取的栅格图进行叠置和属性链接，从而获取每一个Delaunay三角形经济重心的数值。5）以第3步中获取的Delaunay三角形的经济重心为点集，重复2、3、4步进行递归运算，直至所有的点汇于一密集的点群。其中2、3、4步可以通过编程语言C＃或C■等进行循环递归运算。

3 实证研究

3.1 数据处理

本文以四川省为例进行实证研究。使用的四川省各个地市的国内生产总值数据来源于《2006年四川统计年鉴》、《2006年西藏统计年鉴》、《2006年青海统计年鉴》、《2006年重庆统计年鉴》等7省的统计年鉴。鉴于四川省21个县市的行政中心分布于四川中东部，而单纯使用21个地市的国内生产总值数据进行空间插值得到的栅格数据不够准确，故本研究使用甘孜藏族自治州的18个县、凉山彝族自治州的17个县、阿坝藏族自治州的13个县代替以上3个州的行政中心，再加上周边7省40个点，共106个点数据，从而对原始数据进行了加密，提高了最终的插值精度。此外由于研究区域地处西部山区，地形错综复杂，经济发展势必受地形影响很大，因此在插值过程中将地形数据作为辅助影响因子对以上106个点数据进行Cokriging插值，并在ArcGIS 9.3软件的支持下制作了西南地区的国内生产总值插值图。图2是经过裁剪后的四川国内生产总值插值图。

图2 四川省的国内生产总值插值Fig.2 The GDP interpolation of Sichuan Province

3.2 Delaunay三角形剖分

利用C＃或C■等编程语言并结合ArcGIS，使用横向扩张算法对四川省21个次级行政中心形成的点集进行Delaunay三角形剖分。存储结构可采用三角形表和点表构成的双表结构［14，15］。三角形与点的数据结构用C＃语言表达为：

Class Point

｛

public float x；／／顶点的横坐标

public float y；／／顶点的纵坐标

｝

Class Triangle

｛

public int［］points＝new int［3］；public int［］link Tri＝new int［3］；｝

Triangle类中的points是指向3个顶点的索引数组，其元素值为在点集数组中的位置；link Tri为指向3个邻接三角形的索引数组，其元素值为三角形数组中的位置。为了生成三角形之间的邻接关系，也要规定所有三角形的顶点为逆时针排列顺序。这样，只有三角形边的右侧才能有邻接三角形。设3顶点序号为1、2、3，则该三角形的邻接三角形索引的序号等于按逆时针方向第1个共享顶点的序号（图3）。

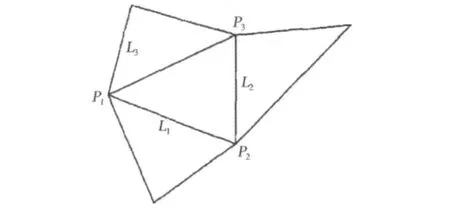
图3 三角形顶点顺序与邻接三角形索引顺序Fig.3 Order of triangle vertices and order of the adjacent triangles

采用以上方法，将四川省21个地市的国民生产总值构成的点集，在C＃中编写代码进行n次迭代并结合ArcGIS的空间分析获取Delaunay三角形的剖分图序列（图4）。

图4 Delaunay三角形的剖分结果Fig.4 The result of Delaunay triangulation of Sichuan

4 结论与讨论

（1）通过GIS的空间插值功能获取研究区域连续的数值曲面，其中采用的克里格插值算法很好地与经济发展与分布的特性相吻合，相关研究表明城市经济对乡村经济辐射和吸引作用的大小与城市聚集程度呈正比，从而更好地解决了传统算法中只考虑时间效应而没有考虑空间效应的弊端。

（2）本研究通过对范围较大的研究区域进行Delaunay三角形的剖分，Delaunay三角形的最小内角及平均形态比最大的性质以及空间插值的算法在一定程度上更符合研究区城市化过程中的经济发展辐射效应这一特点，从而克服了传统的经济重心获取方法在研究大范围区域中因没有考虑城市化过程中的聚集效应和辐射效应而存在很大的误差。而且基于GIS、Delaunay三角形算法在整个求算过程中采用递归方法，每次递归都用不同插值后的数据点集，整个求算过程使用的点数据远远大于初始的点集数量，也克服了当大范围区域次级行政单元较少且分布不均匀时传统的经济重心求算方法所得结果产生的很大误差。

（3）运用基于克吕格插值和Delaunay三角形算法获取经济重心在区域发展差异大、经济发展不均衡的大范围区域要取得相对精确的结果，研究人员对插值过程中模型参数（如偏基台值、块金效应等）的设置很关键，这势必要求研究者对研究区域有比较好的了解，而小范围研究区域则考虑到计算复杂度问题可以直接采用传统的经济重心公式获取。

总之，与传统的方法相比较，新方法无论是在人口重心、产业重心还是其社会指标的重心求算中都有很好的应用。在数据处理方面，由于技术问题，还没有实现整个求算过程的自动化，因此在实现C＃开发的程序与ArcGIS接口这一问题上有待进一步完善。

［1］ 黄建山，冯宗宪.我国产业经济重心演变路径及其影响因素分析［J］.地理与地理信息科学，2005，21（5）：50－54.

［2］ 樊杰，W·陶普曼.中国农村工业化的经济分析及省际发展水平差异［J］.地理学报，1996，51（5）：398－407.

［3］ 李仪俊.我国人口重心及其移动轨迹［J］.人口研究，1983（1）：28－32.

［4］ 包玉海，乌兰图雅，香宝，等.内蒙古耕地重心移动及其驱动因子分析［J］.地理科学进展，1998，17（4）：48－53.

［5］ 周民良.经济重心、区域差距与协调发展［J］.中国社会科学，2000（2）：42－53.

［6］ 徐建华，岳文泽.近20年来中国人口重心与经济重心的演变及其对比分析［J］.地理科学，2001，21（5）：385－389.

［7］ 陈希华.山东省产业重心转移与可持续发展研究［J］.地球信息科学，2001，3（4）：28－29.

［8］ 乔家君，李小建.近50年来中国经济重心移动路径分析［J］.地域研究与开发，2005，24（1）：12－16.

［9］ 朱求安，张万昌，余钧辉.基于GIS的空间插值方法研究［J］.江西师范大学学报（自然科学版），2004（2）：183－188.

［10］ 曾薇，孟祥旭，杨承磊.平面多边形域的快速约束Delaunay三角化［J］.计算机辅助设计与图形学学报，2005（9）：1933－1940.

［11］ 刘永和，王燕平，齐永安.一种快速生成平面Delaunay三角网的横向扩张法［J］.地球信息科学，2008，11（1）：21－25.

［12］ LEE D T，SCHACHTER B J.Two algorithms for constructing a Delaunay triangulation［J］.International Jounal of Computer and Information Science，1980，9（3）：219－242.

［13］ DWYER R A.A fast Divide and Conquer algorithm for constructing Delaunay triangulations［J］.Algorithmica，1987（2）：137－151.

［14］ 袁翰，李伟波，陈婷婷.对构建Delaunay三角网中凸壳算法的研究与改进［J］.计算机工程，2007（7）：70－72.

［15］ ALTMAN E R，KAELI D，SHEFFER Y.Welcome to the opportunities of binary translation［J］.Computer，2000，33（3）：40－45.

Abstract：Deficiency of traditional economy gravity center research and a new method based on GIS and Delaunay triangle are presented in this paper.The calculating methods for traditional economic gravity center have ignored the radiation effects of economic development，aggregation effects and proximity effects resulting from the urbanization process，especially the effects of complicated terrain on economic development.The spatial interpolation algorithm：Cokriging and the multiple iterative operations of the planar triangulation of a set of spatial points combined with GIS can solve the deficiency.The paper elucidates technical process of the new method and receives better effect by taking the GNP of Sichuan Province，which can provide an excellent method for analysis of the gravity center of population and cultivated land as well as other social indexes.

Key words：economic gravity center；Delaunay triangle；spatial interpolation；Kriging

Research on Acquisition Method of Economic Gravity Centre Based on GIS and Delaunay in Complicated Terrain Area

GUO Bing1，2，TAO He－ping1，LIU Bin－tao1，JIANG Lin3
（1.Institute of Mountain Hazards and Environment，CAS，Chengdu 610041；2.Graduate University of the Chinese Academy of Sciences，Beijing 100049；3.Chengdu University of Information Technology，Chengdu 610225，China）

P208

A

1672－0504（2012）02－0055－05

2011－09－16；

2011－11－03

中国科学院知识创新工程重要方向项目“西南山区情势与资源环境安全战略研究”（KZCX2－YW－333）；中国科学院知识创新工程重要方向项目“西南典型山区聚落宜居性与聚落重构研究”（KZCXZ－EW－317）

郭兵（1987－），男，硕士研究生，从事山地生态环境演变、GIS开发及应用与数字山地等研究。E－mail：guobingjl＠163.com