空间目标方向关系的图谱分析方法

魏孔鹏，陈晓勇

（东华理工大学测绘工程学院，江西抚州344000）

空间目标方向关系的图谱分析方法

魏孔鹏，陈晓勇

（东华理工大学测绘工程学院，江西抚州344000）

在地学信息图谱理论的基础上，应用数学形态学原理和方法建立了能够兼顾目标形状、尺寸和距离的方向关系模型，生成方向关系图谱并进行图谱分析。首先将源目标进行形态变换；然后选择方向关系的粒度，用变换后的源目标和参考目标相交区域面积的比值生成图谱，再根据设定的特征值 （如均值、方差、熵等）进行方向关系图谱的分析；最后通过实例验证了该方法的正确性和可行性。

地学信息图谱；方向关系；图谱；空间分析；数学形态学

0 引言

地学空间分析（Geo－spatial Analysis）是基于地学对象的位置和形态特征分析空间数据、研究空间信息分布的特征以及相互关联规律的科学［1］。空间方向关系在空间分析、空间推理、制图综合等过程中起着重要作用，与空间距离、空间拓扑关系同为GIS的重要理论问题［2］。

近年来，国内外学者对空间目标方向关系及其空间定性推理进行了深入研究，提出的主要方向关系模型有：锥形模型［3］、最小约束矩阵（MBR）模型［4］、最小外接矩阵（MER）模型［5］、方向关系矩阵模型［6］和方向Voronoi模型［7］。现有的模型主要是将参考目标划分成若干份，再附加参考框架，忽略了源目标的尺寸、形状、距离等空间特征。按照传统的方向概念，目标之间的方向关系与目标间的距离无关，但当顾及目标的大小和形状后，目标之间的方向关系则与其间的距离相关。图1a描述了距离对方向关系的影响：当目标B逐渐远离A时，方向关系的分布发生明显变化；当A、B无限远时，可视A、B的方向关系为两点之间的方向关系。图1b描述了形状对方向关系的影响：当源目标B比参考目标A的可视域［8］小或者相同时，容易推理出目标A、B的方向关系；但若源目标比参考目标的可视域大，推理则比较困难。图1c描述的是相同形状但不同尺寸的源目标：当源目标比参考目标的尺寸大时，方向关系推理较困难。因此，有必要建立一种新的空间方向关系描述模型，能够全面考虑形状、尺寸、距离等空间目标的特征。

本文用数学形态学原理和方法建立了新的方向关系模型。首先对源目标进行形态变换，选择方向关系的粒度；然后用变换后的源目标和参考目标相交区域面积的比值生成图谱，根据设定的特征值（最小值、最大值、均值、方差、熵）论述图谱的分析方法；最后用实例验证本文所述方法的正确性和可行性。

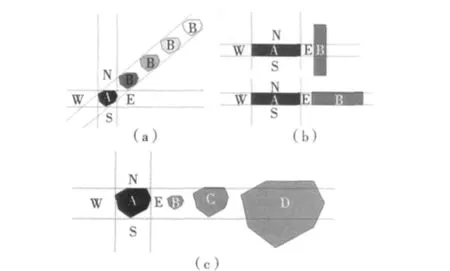
图1 距离、形状、尺寸对方向关系的影响Fig.1 The influence of distance，shape and size on direction relationship

1 图谱的数学描述

地学信息图谱具有图形与谱系的双重特性，是由大量地学数字信息经过图形思维与抽象概括，并以计算机多维与动态可视化技术，显示和揭示地球系统及各要素和现象空间形态结构与时空变化规律的一种手段与方法［9］。近十几年来，许多学者对地学信息图谱的概念、理论和应用做了广泛研究，取得了很多成果［10］。本文将探索方向关系图谱的数学描述方法，并以此为基础进行空间目标方向关系图谱的研究。

数学中将给定的一组元素称为集合（Set）。如果在其元素中，按照指定的规则定义某种结构，则构成相应空间（Space），空间形式和完整性取决于选择的结构。空间中所有线性独立的元素（基元）的集合构成该空间的完备正交基（Basis），空间中任何子集在完备正交基上的特征值分布称为谱（Spectrum），其中单个的特征值称为谱密度。

方向的集合＝｛上、下、前、后、左、右、东、南、西、北、东南、西北、1°、π、…｝；方向的结构可以是二方向、四方向、八方向、十六方向、十二方向（时钟方向）等；方向关系的完备正交基可以是｛前、后、左、右｝，也可以是｛东、南、西、北、东南、东北、西南、西北｝等；方向关系的谱是指在某个粒度下，空间目标方向关系子集在完备正交基上的特征值分布，单个的特征值称为方向关系的谱密度。

2 空间目标方向关系的图谱分析

2.1 方向关系模型的建立

首先，根据实际问题的需求选取α角度值（如1°、3°、5°等）作为方向关系的基元。根据数学形态学原理［11］，目标A以正北方向为起始，沿α角度无限膨胀地进行形态变换，记为A⊕Iαn∞；目标A经过形态变换后若与目标B有交集，则记为：

MBN是指目标A形态变换后与目标B的交集，MBN的值是该区域的像素值；若与目标B无交集，则MBN＝0。

若按顺时针方向，将目标A每隔α角度依次膨胀一周，则目标A共有N次形态变换，其中N＝360°／α。式（1）可推广成：

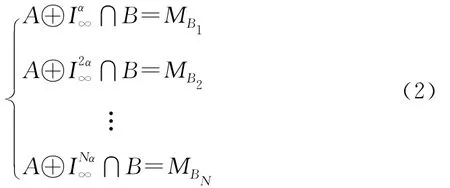
｛MB1，MB2，…，MBN｝为目标A每隔α角度形态变换后与目标B相交区域的集合，MBN的数值为相交区域的像素值。

2.2 方向关系图谱的生成

针对复杂图形，构建方向关系图谱的基本过程如下：

（1）根据方向关系模型，目标A共有N次形态变换，且形态变换后与目标B的交集为｛MB1，MB2，…，MBN｝，其中MBN的非0值集合就构成了方向关系的完备正交基，记为｛M′B1，M′B2，…，M′BN｝。对完备正交基进行归一化处理，并生成谱密度分布，即：

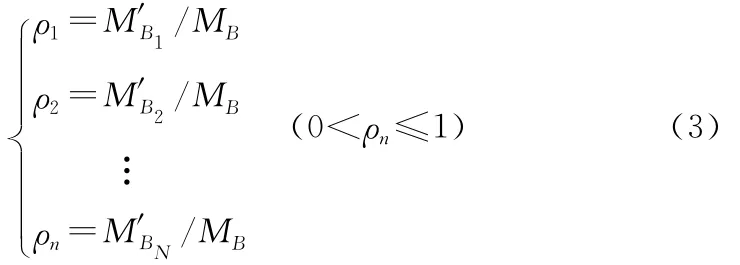
其中：ρ1，ρ2，…，ρn是某一方向的谱密度，则｛ρ1，ρ2，…，ρn｝就是目标A与B方向关系的完备正交基上的谱密度分布，也称为目标A与B方向关系的谱。同理，可生成以B为参考目标的A的方向关系图谱的谱密度分布。

（2）根据谱密度分布，进行谱分析和提取相应的图谱特征（如均值、方差、熵等）。按式（4）分别计算图谱特征：

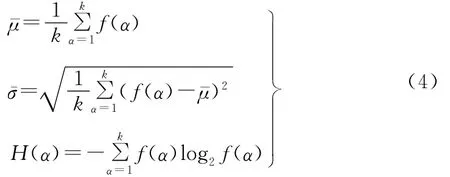
2.3 方向关系图谱的分析

如图2，目标A、B的方向关系图谱生成方式如下：

（1）从正北方向顺时针每隔5°对目标A进行形态变换，与目标B形成的交集为MB，按顺时针方向依次形态变换一周，则共有72次形态变换。

｛MB1，MB2，…，MB72｝的非0值集合构成方向关系图谱的完备正交基，根据式（3）计算该方向关系的谱密度分布（表1）。

图2 空间目标A与B的方向关系模型Fig.2 The direction relationship of target A and B

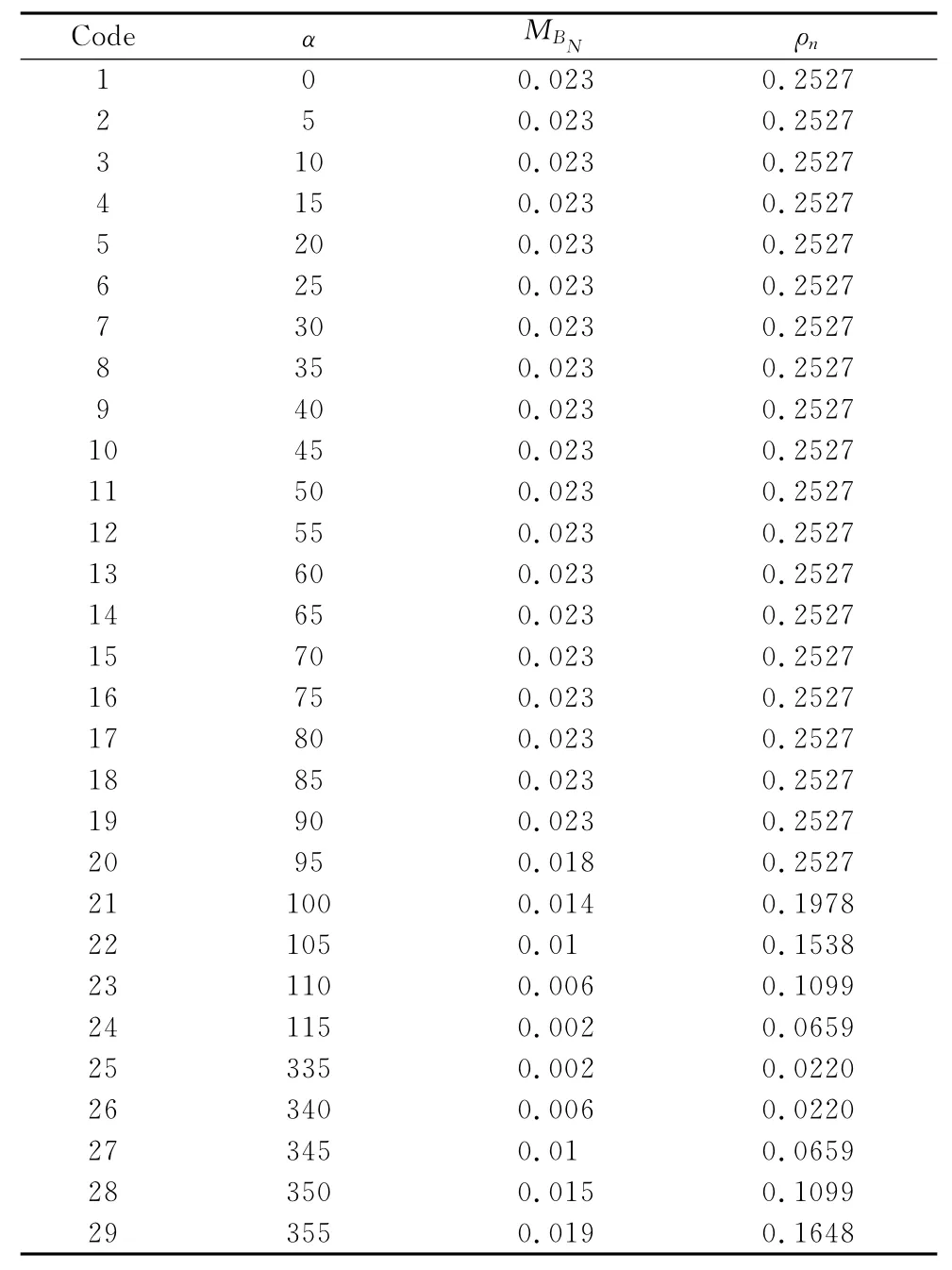
表1 谱密度数据计算处理（A为参考目标）Table 1 Spectrum density computation of experimental data（target A is reference target）

（2）结合已计算出的谱密度，根据式（4）提取相应的图谱特征（表2）。

表2 空间目标A与B的方向关系图谱特征Table 2 The spectrum feature of target A and B

（3）生成目标A与目标B方向关系图谱的谱向量分布，如图3所示。

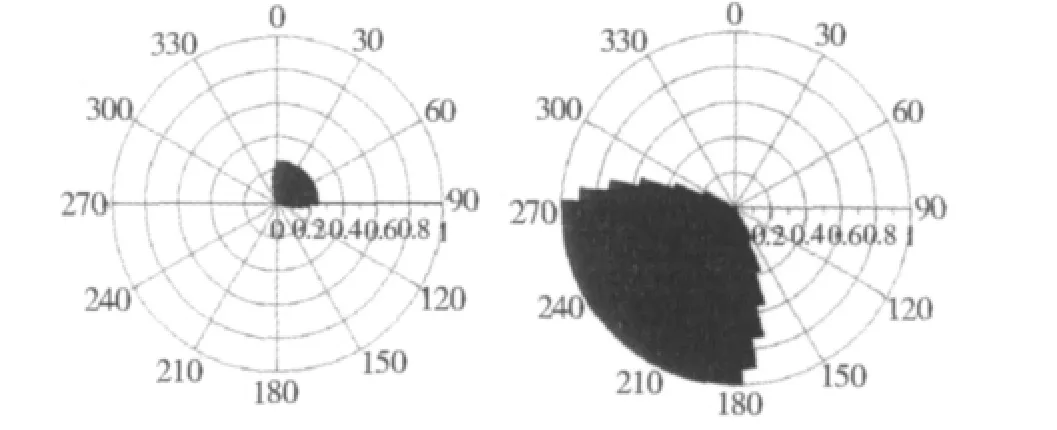
图3 空间目标A与B的谱向量分布Fig.3 A generated sequence of spectrum density distribution for target A and B

3 实例分析

随着大城市中建筑物高度和密度的快速增加，高层建筑物所造成的太阳阴影遮挡及其变化规律是一个迫切需要解决的问题。作为方向关系图谱的一个实际应用，笔者开发了相应的软件系统：根据给定的三维地图和相关参数（如地区的经纬度、日期、时间、建筑物高度和形状等）可生成某一时刻的太阳阴影图；将太阳阴影图与指定的地物集合相交，用阴影面积（或体积）的比率计算此时的图谱密度；根据实际需要选择某一时间间隔，作为方向关系图谱的基元，并以此将一天24小时划分成一个完整序列，生成相应的方向关系图谱，即可实现全天候高层建筑物太阳阴影遮挡的定量解析（图4）。

图4 基于方向图谱的高层建筑物太阳阴影遮挡的全天候分析Fig.4 The analysis of the shadow of the sun－rise buildings around the clock by the direction relationship spectrum

在注册新的商标时，需要审查待注册商标图像与已注册商标图像的相似性，从而决定其是否具有注册资格。由于注册商标的数目不断增加，基于人工商标查询方式难以满足检索的实时性和准确性要求，因此需要建立一种准确、高效的商标图像自动检索系统。具体方法如下：1）初始化二值商标图像，提取图像边缘，计算最小外接圆；2）根据实际需要选取角度平分外接圆，计算每个分块内图像的像素值；3）用各分块内图像的面积比率生成商标图像的方向关系图谱；4）根据谱密度分布和图谱特征检索分类商标，如图5所示。

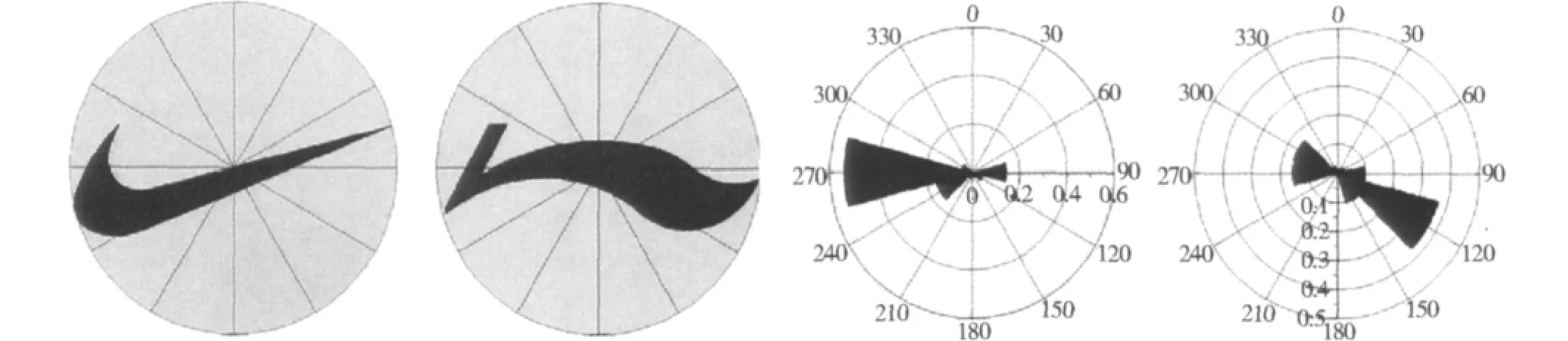
图5 商标图像的方向图谱方法检索分类Fig.5 The analysis of the trademark image classification and retrieval by the direction relationship spectrum

4 结语

陈述彭院士倡导的地学信息图谱，从宏观的“图”关联到微观的“谱”解析，为解决地球信息科学中复杂分析问题提供了新的理论与方法。基于数学形态学原理和方法构建的方向关系模型、图谱及相应图谱分析方法，全面考虑了形状、尺寸、距离等空间目标的特征，实现了复杂空间目标之间的方向关系的完整解析，能够满足实际GIS空间分析应用中的方向关系分析要求。实例验证了本文方法的正确性和可行性。

［1］ 郭仁忠.空间分析［M］.北京：高等教育出版社，2001.1－8.

［2］ FRANK A.Qualitative spatial reasoning cardinal directions as an example［J］.International Journal of Geographic Information System，1996，10（3）：269－290.

［3］ HAAR R.Computational Models of Spatial Relations［R］.Technical Report：TR－478，MSC－72－03610，Computer Science，University of Maryland，College Park，MD，1976.

［4］ PAPADIAS D.Relation－Based Representation of Spatial Knowledge［D］.National Technical University of Athens，1994.

［5］ MUKERJEE A，JOE G A.qualitative model for space［A］.Proceedings of the 8th National Conference on Artificial Intelligence［C］.Boston，MA，1990.721－727.

［6］ GOYAL R.Similarity Assessment for Cardinal Directions between Extended Spatial Objects［D］.University of Maine，Orono，ME，2000.

［7］ YAN H，CHU Y，LI Z，et al.A quantitative description model for direction relations based on direction groups［J］.Geoinformatica，2006，10（2）：177－195.

［8］ 闫浩文，郭仁忠.基于Voronoi图的空间方向关系形式化描述研究（一）［J］.测绘科学，2001，27（1）：24－29.

［9］ 陈述彭，岳天祥，励惠国.地学信息图谱研究及其应用［J］.地理研究，2000，19（4）：337－343.

［10］ 陈燕，齐清文，杨桂山.地学信息图谱的基础理论探讨［J］.地理科学，2006，26（3）：306－307.

［11］ 陈晓勇.数学形态学与影像分析［M］.武汉：测绘出版社，1991.

Abstract：This paper presents a new method for describing directional relations based on their graph－spectrums by using the theory of the Mathematical Morphology.Directional relation graph－spectrums are generated based on the ratio of intersection area by original target and reference target which has been morphological transformation.Graph－spectrum analysis of directional relations is described according to a set of selected features，such as minimum，maximum，mean，standard deviation and entropy.Finally these new measures are experimentally evaluated.

Key words：Geo－information graph－spectrum；directional relations；graph－spectrum；spatial analysis；mathematical morphology

Graph－Spectrum Analysis on Directional Relations of Spatial Targets

WEI Kong－peng，CHEN Xiao－yong
（College of Surveying and Mapping Engineering，East China Institute of Technology，Fuzhou 344000，China）

P208

A

1672－0504（2012）04－0029－04

2011－12－28；

2012－02－28

国家自然科学基金项目（40940011、41161069）

魏孔鹏（1982－），男，硕士研究生，主要从事地学空间分析的理论与应用研究。E－mail：kpwei＠ecit.edu.cn