基于感知无线电非合作博弈功率控制算法的研究★
2012-09-12陈媛媛王晶晶
陈媛媛, 王晶晶
(海南工商职业学院,海口 570203)
0 引言
感知无线电作为未来无线通信的发展方向之一,能充分利用现有频谱资源实现频谱共享,提高频谱利用率,可以实现外部环境认知,信道状态及容量预测,功率控制和动态频谱接入等。它能够使非授权用户与授权用户共享频谱, 且保证不会干扰授权用户的正常通信。每个感知用户(非授权用户)的发射功率是造成其他用户干扰的主要原因, 因此功率控制是感知无线电系统的关键技术之一。
David Goodman等人[2]提出一种非合作博弈功率控制( non-cooperative power control game )的模型,并证明其存在纳什均衡。但均衡解并不一定最优,进而研究了基于代价函数和非线性代价函数的博弈功率控制算法[3]。博弈论[4]是一种用于分析决策过程中参与者交互作用的数学工具,并为参与者制定利益最大化决策。早期主要应用在经济学领域当中,近年来在各个学科中都有广泛的使用。
本文将非合作博弈的思想应用于感知无线电系统的功率控制中,在考虑主用户和感知用户的通信要求前提下,主要研究感知无线电环境下感知用户功率控制问题,以实现系统资源分配最优,借鉴文献[2-3,5-6]的研究,提出一种改进的基于非线性代价函数的算法,并对算法进行了仿真分析,实现了对不同用户发射功率的有效控制,以达到最佳频谱利用率。
1 系统模型
本文拟设计在一个单基站的小区内,有若干个感知用户共享一段频谱。这里不考虑感知用户对主用户的干扰,因为感知无线电最重要的前提是要保证主用户的通信质量,假设主用户一旦需要重新占用自己的授权频段,感知用户就必须退出网络把频段还给主用户,因此感知用户就不会对主用户造成干扰。所以本文认为只考虑感知用户之间的功率控制问题是今后研究的主方向。各感知用户的接入选择为CDMA制式,因为目前主要的接入方式有3种:CDMA、FDMA和TDMA。而在后2种接入方式中,TDMA方式是在不同的时隙进行信号的传输,每个时隙内都只有一个用户在进行信息传输,即各用户之间的干扰是不存在的,更谈不上功率控制问题,而FDMA方式的相邻信道干扰又比较小,考虑功率控制并无太大实际意义,故选用CDMA系统接入方式。
2 算法设计
2.1 非合作功率控制博弈算法(NPG算法)
David Goodman提出了一种无线数据网络中的非合作功率控制博弈算法。其效用函数如式(1)。
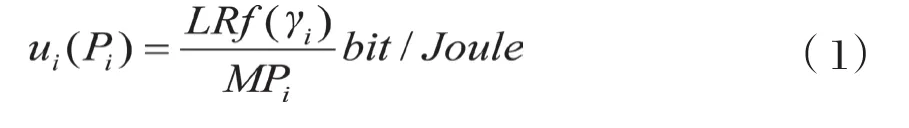
效用函数即为消耗每单位焦耳的能量所能接收到的信息比特数。式(1)中: M为每个数据帧中传输的总比特数;L为每个数据帧中的信息比特数;R为信息传输速率; pi为第i个用户的发射功率;γi为第i个用户的SIR;而第i个用户的SIR又可定义为式(2):

假设CDMA系统中采用Non-FSK调制方式,那么效率函数f(γi)即接收机接收到的有用信息的效率可表示为式(3),式(4)中 Pe为误码率 (BER)。


在非合作功率控制博弈模型中,每个用户都试图最大化自己的效用函数,可以表示为式(5),通常pi是用户i的策略空间集合,p-i表示除了用户i以外的所有其他用户功率的策略空间集合。用户的收益最大化,不仅由用户自身的发射功率水平所决定,同时也受到其他用户发射功率的影响,因此所有用户最大化各自收益的过程就是由一个非合作的博弈过程。研究表明[2],此算法在博弈过程中纳什均衡存在的条件下,最终收敛于纳什均衡点。
2.2 基于代价函数的NPGP算法
采用NPG方法所获得的均衡解并不是最优的,因为非合作关系导致每个用户都致力于通过调整发送功率以实现自身效用的最大化,却忽视了对系统中其他用户产生的干扰。于是Goodman等人又提出了一种基于代价函数的NPGP (Noncooperative Power control Game with Pricing)算法。用户的效用函数可以表示为:

其中,随线性增长的代价函数ci( pi, p-i) =cpi,c为常数,称为代价因子。即效用函数可表示为:
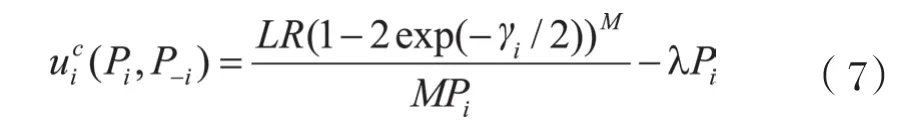
那么NPGP的博弈过程就可以表示为:
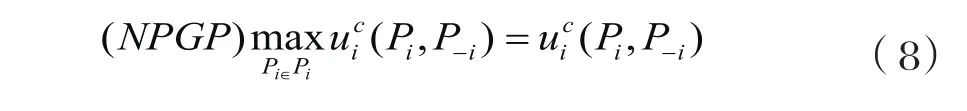
仿真表明,在引入代价函数以后各用户稳定工作在相对更低的发送功率下,具有更好的使用性能。
2.3 基于非线性代价函数的NPGP-NL算法
在NPGP模型中, 代价函数只考虑到感知用户的发射功率。而在感知用户的接收方,信号质量的好坏还与噪声、干扰、路径增益等参数相关。因而线性的发射功率代价函数并不能充分公平地惩罚各感知用户[7-8]。从式(8)的结构可以看到,代价函数的选用是线性的,而本文则考虑设计一个既能适当体现公平性, 又相对简单便于数学分析的非线性代价函数(Non-cooperative Power control Game with Non-liner Pricing)算法。用户在NPGP-NL算法下的效用函数表示为:
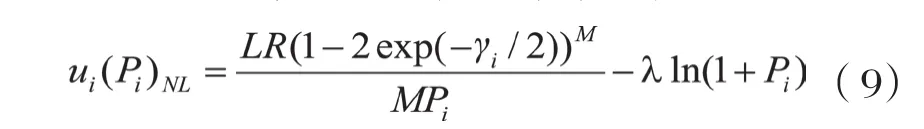
从式(9)中可以看出,用户i的效用函数会随着自身的发射功率pi的增大而减小,这样就避免了单个用户为了提高自身的效用而不断增大自己的发射功率的目的,从而更好地利用了频谱资源。研究证明NPGP-NL算法满足超模博弈中的条件,存在纳什均衡点。具体算法步骤如下:
2)令 L=L+1,根据已知条件 pi(L-1),i∈N,计算在给定其他用户发射功率条件下,所有用户i∈N使自己效用函数达到最大值时所对应的最优发射功率,表达式为:
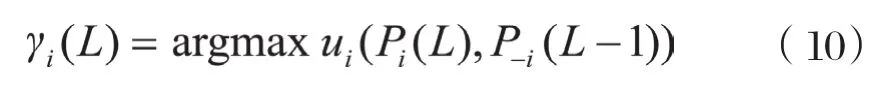
3)最后,令pi(L)=min(ri(L)),即为用户i的最优发射功率。
3 数据仿真及分析
系统环境为单基站的CDMA小区网络,假设小区内有6个感知用户,利用如下的参数进行仿真,结果如图1、图2所示。实验系统参数:每帧总比特数M=40,每帧信息数据比特数L=32,系统扩频增益G=100,R=10 Kb/s,调制方式为Non-FSK,噪声功率σ2=5×10-14W,用户的最大发射功率为2 W,用户i的链路增益hi=9.7×10-3/d-4,仿真工具采用MATLAB。

图1 各算法的发射功率比较
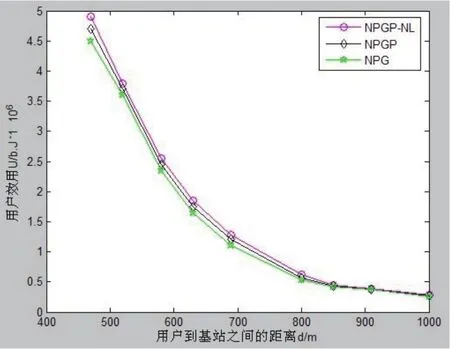
图2 各算法的效用比较
从图1、图2中可以看出,新的NPGP-NL算法在整体的用户效用和发射功率控制方面都比NPG和NPGP算法有一定的提高,既降低了感知用户的发射功率,又相应提高了效用函数的性能,最终实现系统各用户效益最大化的要求,进而实现系统资源的最优分配。
图3比较了3种博弈的信干噪比(SINR)。NPG各用户信干噪比基本相同,保证了接收端的绝对公正。NPGP由于其代价函数的统一性,对距离相对较远,发射功率较大的用户惩罚过大,以至其信干噪比呈明显下降趋势。而NPGP-NL通过合理的选择惩罚因子和其他参数以及纳什均衡点的唯一性,对各个距离上的感知用户相对公平,使其性能相近,实现最优功率分配。

图3 各算法信干噪比的比较
4 结论
本文主要讨论感知无线电系统中基于非合作博弈理论的分布式功率控制算法,在Goodman等人提出的NPG和NPGP模型的基础上,综合考虑主要用户对次要用户的干扰和次要用户之间的干扰,提出了一种改进的非线性代价函数的算法。通过仿真分析可以看出本文提出的NPGP-NL算法在提高感知用户效用的基础上,还一定程度上兼顾了系统的公平性,提升了感知用户的性能,实现了对不同用户发射功率的有效控制,使系统性能明显提高,达到了预期设计目标。
[1]FCC Spectrum Policy Task Force, Report of the spectrum efficiency working group [EB /OL][2009.09.11].http: // www.fcc.gov /s ptf/reports.html
[2]GOODMAN D, MANDAYAM N.Power Control for w ireless data [J].IEEE Personal CommunMag,2000,7: 48-54.
[3]SARAYDAR C, MANDAYAM N, GOODMAN D.Efficient power control via pricing in w ireless data networks[J].IEEE Trans Commun,2002,50 (2):291-303.
[4]DAMME,ER IC V.Game Theory:The Next Stage[M].Tilburg:Tilburg University,995.
[5]SETOODEN P, HAYK IN S.Robust transmit power control for cognitive radio[J].Proceedings of the IEEE,2009,97(5):915-939.
[6]ZHOU Pan,YUAN Wei.Joint power and rate control in cognitive radio networks: A game theoretical app roach[C].IEEE International Conference on Communications,Piscataway:IEEE,2008:3296-3301.
[7]M ITOLA J.Cognitive radio:An integrated agent architecture for software defined radio [D].The Dissertation for Doctor of Technology,Royal Institute of Technology (KTH),2000.
[8]HAYKIN S.Cognitive radio: Brain-empowered wireless communications[J].IEEE Journal on Selected Areas in Communications,2005,23(2):201-220.
