TC11钛合金整体叶盘锻件组织均匀性评价方法
2012-09-12杨艳慧罗子健
杨艳慧, 刘 东, 罗子健
(西北工业大学材料学院,西安 710072)
盘件是涡轮机械的关键部件,航空、航天发动机用盘件一般采用高温合金、钛合金等难变形材料进行制造,其组织均匀性对盘件的使用性能具有重要影响[1]。因此,科学地进行盘锻件组织均匀性评价和控制一直是难变形材料盘锻件制造技术的重要研究方向。由于难变形材料锻件的组织状态与变形均匀性关系密切,国内外许多学者致力于盘锻件变形均匀性的评价和控制研究工作。赵国群[2,3]等提出了描述锻件变形均匀性的指标,并对H型截面盘锻件进行预成形设计。作者也曾就GH4169合金涡轮盘锻件变形均匀性表征方法进行了研究,并提出了提高锻件变形均匀性的预成形优化方法[4,5]。在锻件组织均匀性方面,赵国群[6]等人应用Yada模型,进行了面向微观组织优化的预成形设计。然而,对于高温合金和钛合金等难变形材料,热加工过程中会同时发生或相继发生多个物理冶金过程,例如,相变、动态再结晶、亚动态再结晶以及静态再结晶等。简单地运用现有的组织演化模型[7~10]并不能获得理想的组织均匀性评价效果。
本工作基于Taguchi方法,提出了以锻件内部热力参数为基本变量的损失函数,从而探索盘类锻件组织均匀性的评价方法。以TC11钛合金整体叶盘为例,应用所建立的损失函数对整体叶盘锻造过程进行有限元数值模拟和锻件组织均匀性评价,并将数值模拟结果与试验结果进行了对比。
1 损失函数LF的定义
质量控制理论中,加工工艺的设计过程可分为三个阶段:系统设计,参数设计和容差设计。根据Taguchi方法[11],在容差设计阶段,为保证产品质量,可通过定义质量损失函数(LF)来确定可控参数的容许变动范围。本文建立评价组织均匀性的损失函数过程如下:
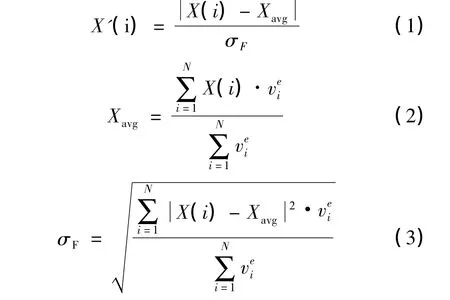
第一步,借助有限元网格系统,定义以下公式确定单元i的热力参数X(i)的分布均匀程度:式中Xavg为热力参数的体积平均值;N为工件内的单元总数;vei为单元i的体积;X'(i)表征单元i内的热力参数分布均匀程度。
第二步,按下式定义单元i的质量损失贡献因子λi:
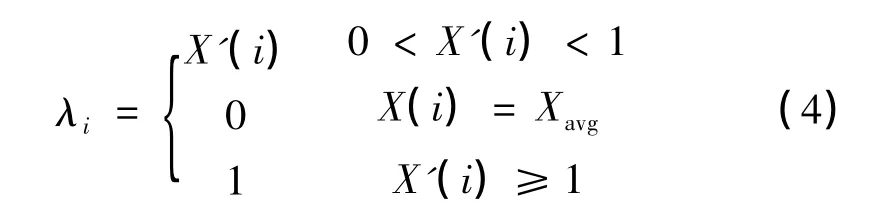
在有限元计算的某一加载步,如单元i的热力参数值X()i与Xavg相等时,X'(i)=0。此时,质量损失贡献因子λi=0,即对质量损失贡献为0;否则,0<λi≤1,其大小表示单元i对质量损失的贡献。
第三步,按下式确定单元i的质量损失函数LF()i:
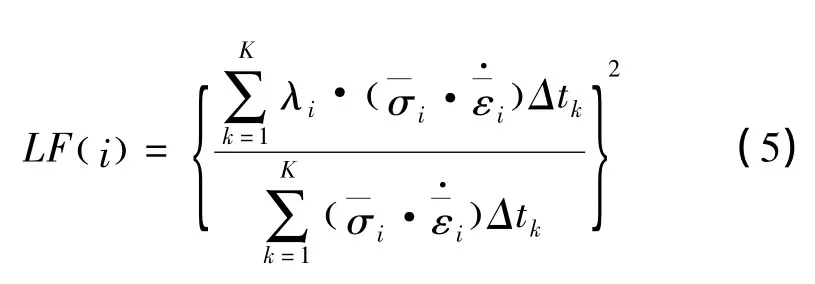
式中K为数值模拟过程中总的加载步数;Δtk为第k加载步的时间步长;分别为单元i的等效应力(MPa)和等效应变速率(s-1)。
第四步定义整个工件的损失函数:

式(6)定义的质量损失函数的取值区间为[0,1]。从式(1)~(5)可以看出,质量损失函数值越小,锻件的热力参数分布均匀性越好,相应的组织状态分布越均匀。
2 TC11钛合金整体叶盘锻造过程数值模拟
整体叶盘是现代航空发动机特有的一种先进整体构件,一般由叶片和盘体两大部分构成,锻件型面复杂,各部位的组织均匀性不易保证。因此,本文以发动机用TC11钛合金整体叶盘为典型对象,探索采用质量损失函数方法进行锻件组织均匀性评价和控制的科学方法。图1所示为TC11钛合金整体叶盘锻件的外形和截面图。整体叶盘的锻造过程在SPKA11200型高能螺旋压力机上完成,主要锻造工艺参数为:始锻温度为β转变温度以下30°C,模具温度260°C,转运时间20s,共锻造3火次,每火次打击5 锤,打击能级分别为 0.45,0.75,0.75,0.85,0.9。锻造过程数值模拟用相关参数如下:摩擦因子为0.25,工件与模具之间的换热系数为20W·m-2·K-1(锤击过程)和 2W·m-2·K-1(锤击间隙),工件与环境的换热系数为0.018 W·m-2·K-1。

图1 整体叶盘锻件结构图Fig.1 Sketch map of the blisk forging
3 数值模拟结果分析
图3所示为质量损失函数LF值在锻件内的分布情况。从图3可以看出,锻件毛边、盘体轮毂部位的LF值较大,图3b中叶片边缘以及锻件与下模接触部位的LF值也较大。整体叶盘锻件大部分体积内的质量损失函数LF值较小(低于0.3)。
据式(5)和式(6),LF值不仅取决于锻件内所有质点的λ值,还与热加工历史有关。因此,图4给出了四种情况下锻造过程中LF值随加载步数的变化曲线。从图可以看出,对于情况1和情况3,质量损失函数LF的值随着锻造过程进行逐渐增大,并且第一火中LF值增加幅度大。其原因是,变形前工件内的等效应变和等效应变速率分布是均匀一致的(均为0),随着变形过程进行,工件不同部位发生不同程度的变形,加之随着锻造过程的进行,材料流动愈来愈剧烈,使得其等效应变和等效应变速率的分布均匀性越来越差。对于情况2,在工件变形开始前经历了转运过程,温度分布均匀性变差,在变形过程中由于变形热效应以及摩擦产生热量引起某些部位温度上升,通过热传导使锻件内温度分布均匀性得到一定改善,因而,LF曲线略有下降。而情况4中LF随加载步数的变化情况是情况1、情况2和情况3的LF变化的综合反映。
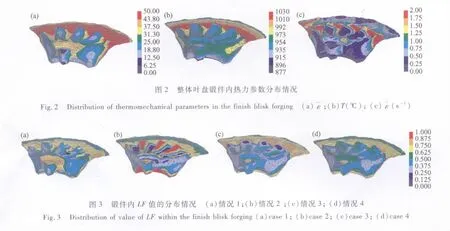
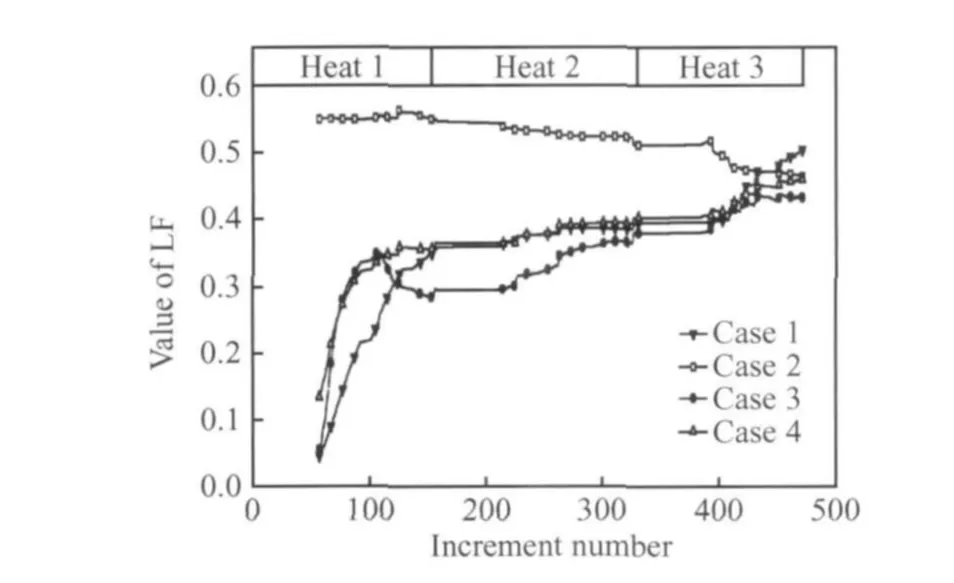
图4 锻造过程中LF随加载步数的变化曲线Fig.4 LF value-step curves of the forging process
4 数值模拟结果与生产实际数据对比
对于TC11钛合金[12],当变形达到一定程度时(大于50%,或等效应变大于0.9左右),合金进入稳态变形阶段时,合金中α晶粒尺寸及其相含量基本保持不变,组织状态主要由温度确定。本工作中四种情况的损失函数LF分别以¯ε,T,¯ε·和三者的代数平均做为基本变量,未考虑合金进入稳态变形后TC11钛合金组织状态演化特点。因此,本研究中情况2可用来评价TC11钛合金的组织均匀性。锻件经热处理后,按照图5所示的位置以及距离锻件边缘23mm处(考查点No.9)的毛边部位切取试样进行金相试验,以考查锻件内的组织均匀性。图6给出了四种情况下锻件本体部位考查点的损失函数LF值对比情况。从图可以看出,除情况1外,大部分考查点的LF数值接近,在0.3~-0.44范围之内,尤其是情况2各点LF值变化较小(参见图6中的折线)。实际上,对于情况1也只是No.5考查点的 LF 值较大,为0.68(远高于 0.33 ~0.44)。根据有限元模拟结果,No.5考查点的应变为1.28(大于0.9),该考查点已处于稳态变形阶段。
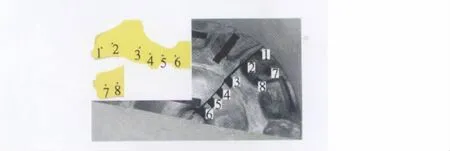
图5 取样点位置示意图Fig.5 Locations of the measured points
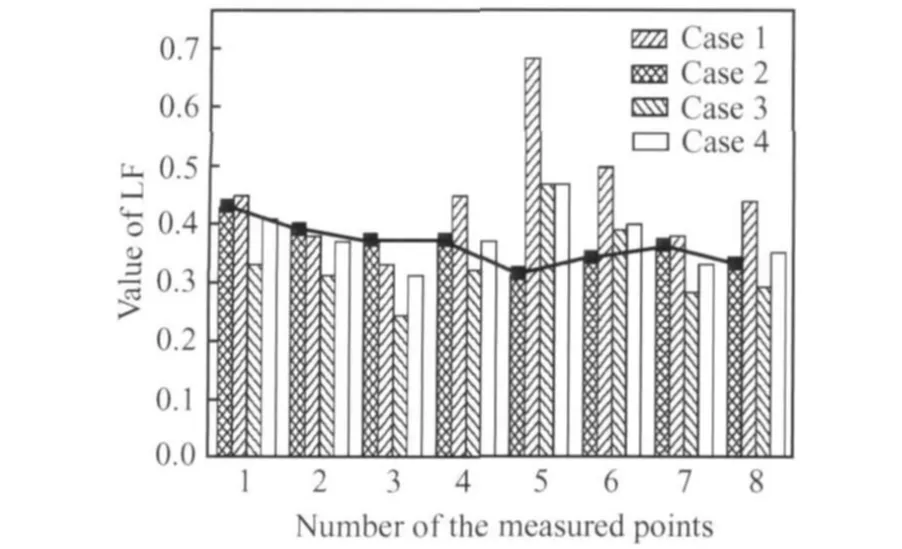
图6 不同考查点处的损失函数值Fig.6 Values of LF for the measured points
图7给出了各考察点的微观组织照片。从图可以看出,前8个考查点的组织为等轴组织:转变β基体上均匀分布着40% ~50%的等轴α相,且α晶粒大小均匀,平均晶粒尺寸约为15μm。根据 HB 5264—1983中给出的TC11钛合金显微组织分类评级图,此8个考查点均可评定为3级,级差为0,满足该锻件的技术条件要求。毛边处(No.9)的微观组织(图7(i))中α相含量明显减少,并且出现了少量片状α相。根据HB 5264—1983可定为5级,与锻件本体部位考查点的显微组织的级差为2级。其原因是,在锻造过程中该考查点处的变形剧烈,热效应明显,使得该处实际温度接近或达到了相变温度,α相含量减少,形态也由等轴转变为长条状。根据有限元数值模拟结果可得到相同的结论,No.9的LF值较大为0.68(情况2),说明此部位的微观组织较锻件主体的差异大。

图7 取样点处的微观组织Fig.7 Optical micrographs of some measured points (a)No.1;(b)No.2;(c)No.3;(d)No.4;(e)No.5;(f)No.6;(g)No.7;(h)No.8;(i)No.9
5 结论
(1)基于FEM数值模拟和Taguchi方法,提出应用损失函数方法对盘件组织均匀性进行评价的方法。对于TC11钛合金整体叶盘锻件,应用情况2建立的质量损失函数贡献因子得到的损失函数的评价结果与实际生产得到的锻件内组织均匀性一致性好。
(2)对于TC11钛合金整体叶盘锻件,当质量损失函数值在0.33~0.44范围内时(情况2),锻件的组织均匀性能满足技术条件要求。
[1]李成功,傅恒志,于翘,等.航空航天材料[M].北京:国防工业出版社,2002:64-99.(LI Cheng-gong,FU Heng-zhi,YU Qiao,et al.Aerospace Materials Beijing.National Defence Industry Press,2011:64—99.)
[2]赵新海,赵国群,王广春,等.锻造过程优化设计目标的研究[J].锻压装备与制造技术,2004(1):48-52.(ZHAO Xin-hai,ZHAO Guo-qun,WANG Guang-chun,et al.Research on the establishment of objective function in forging otimization design[J].China Metalforming Equipment and Manufacturing Technology,2004(1):48 -52.)
[3]ZHAO G Q,WRIGHT E,GRANDHI R V.Preform die design in metal forming using an optimization method[J].Int J Numer Methods Eng.1997,40(7):1213-1230.
[4]杨艳慧,刘东,罗子健.应用基于FEM的预成形最优化方法提高锻件变形均匀性[J].航空学报,2005,26(6):764-767.(YANG Yan-hui,LIU Dong,LUO Zi-jian.Improving the deformation uniformity within forgings by applying preformed optimization based on FEM[J].Acta Aeronautica et Astronautica Sinica,2005,26(6):764 -767.)
[5]YANG Yan-hui,LIU Dong,LUO Zi-jian.Optimization of preform shapes by RSM and FEM to Improve deformation homogeneity in aerospace forgings[J].Chinese Journal of Aeronautics.2010,23(2):260-267
[6]管婧,王广春,赵国群.基于有限元灵敏度分析的锻造成形微观组织优化设计[J].塑性工程学报.2007,14(6):6-10.(GUAN Jing,WANG Guang-chun,ZHAO Guo-qun.The microstructure optimal design using sensitivity analysis methods in forging process[J].Journal of Plasticity Engineering.2007,14(6):6 -10.)
[7]SELLARS C M,WHITEMAN J A.Recrystallization and grain growth in hot rolling[J].Matal Science.1979,13(3-4):187-194
[8]YADA H,SENUMA T.Resistance to hot deformation of steel[J].J JSTP,1986,27:33 -44
[9]KOPP R,KARNHAUSEN K,DE SOUZA M M.Numerical simulation method for designing thermomechanical treatment illustrated by bar rolling scand[J].J Metal 1991,20:351-363
[10]SHEN G S,SEMIATIN S L,SHIVPURI R.Modeling microstructural development during the forging of wasPaloy[J].Metallurgical and Materials Transactions(A).1995,26:1795-1803
[11]SRINIVASAN R J,CHARDHARY A.Applying numerical taguchi optimization to metal forming[J].JOM.1990,42(2):22-23.
[12]陈慧琴,林好转,郭灵,等.TC11钛合金高温流变行为及组织演变[J].航空材料学报.2007,27(3):1-5.(CHEN Hui-qin,LIN Hao-zhuan,GUO Ling,et al.Hot deformation behavior and microstructure evolution of TC11 titanium alloy[J].Journal of Aeronautical Material.27(3),2007:1 -5.)
