PISA中国试测研究的评分者效应分析对高考网上阅卷的启示
2012-09-11张文静
王 蕾,张文静
【统计应用研究】
PISA中国试测研究的评分者效应分析对高考网上阅卷的启示
王 蕾1,张文静2
(1.教育部考试中心,北京100084;2.北京师范大学发展心理研究所,北京100875)
针对PISA 2009中国试测研究主观题评分环节所采用的多重编码设计,分析在阅读、数学和科学领域的评分中是否存在评分者效应。根据多侧面Rasch模型方法,分别对这三个领域进行评分者主效应的分析。结果显示:阅读和科学领域中,评分者之间的严苛度/宽松度差异非常显著;而数学领域中,评分者之间的严苛度/宽松度差异较小。最后,探讨了这些结果的可能原因以及对高考网上阅卷评分借鉴的建议。
评分者效应;严苛度/宽松度;PISA;多重编码;高考网上阅卷
一、问题提出
Scullen、Mount和Goff将评分者效应(rater effects)界定为“一种导致成绩评定等级系统变异的效应类别,在某种意义上,评定的等级与评分者相关,而与被评分者的真实表现无关。”[1]换句话说,评分者效应与欲评估的结构或特质无关,从而影响了评估的信度和效度[2][3]66-70。
在实际情境中,评分者效应非常普遍。一旦涉及多个评分者评定被评分者的表现,评分者效应很容易随之出现。例如,奥运会中多个裁判员评价运动员的表现;企事业单位或公司的管理者评判面试申请者与工作岗位的匹配性;大学根据申请者的材料判断其能否获得奖学金;教师根据学生对主观题的作答进行评分等。研究认为在评分过程中,有三种潜在的偏差或误差来源:评分量尺(rating scales)、评分程序(rating procedure)和评分者(raters)。Cronbach指出,评分活动是“复杂而又易犯错的认知过程”。Thorndike和Hagen认为评分者的认知过程是“黑箱”(black box):“评分是一个评估总结的过程,评分者使用其‘内部计算机’即过去或现在的经验,对输入的数据以一种复杂而又不确定的方式加以处理,从而得到最终的判定”[4]。因此,最大限度地减少评分偏差是任何评估项目,特别是大规模教育考试中需要解决的重要课题之一。通常采用的措施包括严格选拔评分者、对评分者进行培训以及监控评分过程等。
Myford和Wolfe总结了四类常见的评分者效应:严苛度/宽松度(severity/leniency)、晕轮效应(halo effect)、中心化趋势(central tendency)和全距限制(restriction of range)[4]。除此之外,还有其他一些类型的评分者效应,由于它们较难被检测或测量,因此甚少提及,如不精确性、逻辑错误、对照错误等。Cronbach认为与其他类型的评分者效应相比,严苛度/宽松度是评分者在评分过程中的最严重错误[4]。所谓严苛,指某些评分者倾向于给出较低的分数;相反,宽松的评分者倾向于给出较高的分数。本研究的关注对象是在多个评分者存在的情况下,对考试中的主观题(需要考生自己用文字写出答案)进行评分的严苛度/宽松度。以高考为例,每个科目都有大量主观性试题,它们非常容易受到评分者的知识水平、综合能力、爱好、情绪、疲劳等主观因素的影响。不光不同评分员之间存在差异,同一个评分员在不同时间也具有不稳定性。为消除评分者效应,常用的办法是对评分者进行培训,或对于相同的考生进行多人评分。然而,有研究表明,无论如何进行事前培训,评分者也无法在严苛度/宽松度上保持一致[5]。也有研究者使用Kendall和谐系数等考查评分者之间的一致性,但作用非常有限,因为这类评分者一致性系数属于事后检验,对考生得分不会产生校正作用[6-7]。因此,实际考试评分中非常需要能够对考生得分及时进行统计校正的方法。多侧面Rasch模型(many-facet Rasch model)是可以提供解决方案的模型之一。Rasch模型属于测量理论中项目反应理论(item response theory)的一种,它认为考生在某个题目上的正确作答概率是考生的某种潜在心理特质(latent trait)和题目难度的函数[8]122-125。多侧面Rasch模型是对Rasch模型的扩展,通常适用于在模型中考虑多个侧面(如评分者、考试形式等)的情况,该模型所提供的统计分析框架在估算各个侧面的测量值时,将各个侧面之间的相互作用进行了区分和隔离,因此,可以消除主观评分中各个方面的因素对于评分结果的影响,提高评分结果的信度[9]80-85,应用这个框架也可以提高测量的信度[10]。
本研究拟使用多侧面Rasch模型考察PISA(Program for International Student Assessment)2009年中国试测研究中,主观题评分的评分者严苛度/宽松度是否存在显著差异。其中多侧面Rasch模型的数学表达式通常为:
ln(Pnijk/Pnijk-1)=Bn-Dj-Cj-Fk
其中Pnijk是指作答者n在题目i上被评分者j评定为k的概率,Pnijk-1是指作答者n在题目i上被评分者j评定为k-1的概率,Bn是指作答者n的潜在特质水平,Dj是指题目i的难度,Cj是指评分者j的严苛度,Fk是指量表类别k相对于量表类别k-1的难度。
本研究主要有两个目的:一是考察在对PISA 2009中国试测研究的阅读、数学和科学题目进行评分时,评分者之间的严苛度/宽松度是否存在差异;二是考察多重编码和多侧面Rasch模型分析对高考网上阅卷评分实践的意义。
二、数据
(一)PISA简介
PISA是经济合作与发展组织(OECD)于1997年发起的一项监测15岁在校学生学习质量的比较研究项目,旨在评价义务教育阶段结束时,学生是否具备参与未来社会所必需的知识和技能。该项目自2000年开始每隔三年实施一次,评价领域包括数学、阅读和科学素养,每次侧重一个领域,依据评价年命名。PISA 2000、PISA 2003和PISA 2006的主评估领域分别是阅读、数学和科学,PISA 2009的主评估领域则又回归到阅读[11]18-24。
(二)PISA 2009中国试测研究数据
中国先后于2006年和2009年两次开展PISA试测研究。PISA的题目类型有选择题和开放式简答题两种。开放式简答题即为主观题。PISA采用两种评分方式,一种称单独编码(single coding),即每个题目仅由一个评分员评阅;另一种称多重编码(multiple coding),即每个题目由多个评分员评阅。多重编码的目的就是为了考察评分员使用评分标准的一致性程度。
1.抽样程序
PISA2009中国试测采用三阶段分层随机抽样设计,三个阶段分别是:省(自治区、直辖市);学校;学生。
第一阶段完成省(自治区、市)的选择。在保证全国15岁学生代表性的基础上,兼顾自愿参加的原则,参照各省(自治区、市)的综合人文、经济及教育指标,兼顾课改省,在东、中、西部各选择3~4个省(自治区、市)。最后共10个省(自治区、市)参加了此次研究。第二阶段完成学校层面抽样,通过“是否特殊教育学校”和“是否非汉语教学”这两类信息将特殊教育学校和非汉语教学学校排除在抽样范围之外,然后选取三个分层变量:学校的地理位置(城市、县镇和农村)、学校的性质(公办学校、民办学校)、学段(初中、高中和完全中学)。按照这三个维度设计了抽样框架,10个省(自治区、市)据此框架上报了本地区所有包含15岁学生学校的统计信息。按照PISA抽样的基本要求,每个地区各分配了60所学校的样本量。为确保每名学生被抽取到的概率相同,保证样本的充分代表性,减少抽样误差,采用了PPS抽样方法,即学校被抽取到的概率与其所含15岁学生的数量成正比,以保证每名学生被抽取到的概率相同,保证抽样数据的代表性和所得结论的可推广性。第三阶段完成学生样本的抽取。以完全随机抽样的原则从10个省(自治区、市)的587所学校各自中抽出35名15岁学生作为学生样本,15岁学生总数不足35人的学校中所有15岁学生全部参加。数据还将出生年月不符合要求的学生、智残学生和外籍学生数据排除在抽样范围外,最终共有来自587所中学的152 265名学生被纳入样本,有效地代表了10个省(自治区、市)18 550所学校的6 583 212名15岁在校学生总体。
2.研究对象
PISA 2009中国试测研究抽样学生被随机分配完成OECD提供的13个试题册中的1个,评分前从这13个试题册中各抽取100个拷贝共计1 300个试题册用于多重编码。PISA的每个试题册由4个子题本构成,这些子题本来自三个领域(其中阅读共7个子题本,数学和科学各3个子题本),根据矩阵取样设计,不同子题本的组合构成了13个试题册。多重编码并不是对整个试题册进行评分,而是从每个试题册中选取特定子题本的题目由多个评分者评阅。表1是PISA2009中国试测研究选用题册子题本组成。

表1 PISA2009中国试测研究选用题册子题本组成表
3.评分者
共有50名评分者参与PISA 2009中国试测研究的阅卷工作。这些评分者均为来自某师范院校教育或心理学专业的硕士研究生,其中五分之四为女生,32人参与了多重编码的工作。之所以选择他们作为PISA 2009中国试测研究的评分者,出于以下两个方面的考虑:首先,本次试测研究覆盖范围较广,如果由学科专家或教师评分将导致成本过大或时间过长,不利于整个项目的顺利开展;第二,硕士研究生接受过较高水平教育,对新事物(如PISA的评分方式)有较强的接受和学习能力。这些措施和考虑均得到OECD/PISA专家组的认同。
4.评分设计
评分前,首先由国外专家对评分者进行培训。评分过程采用全程质量监控程序以保证评分者使用编码指南的一致性。质量监控程序为,每5个评分者由一个学科教师或专家监控;每25个评分者由2个高级学科专家监控;最后,由1个权威学科专家监控整个编码评分的质量。
根据单一编码设计,50个评分者将评阅所有三个领域的题目;而在多重编码设计中,32个评分者通过领域间的链接设计也将评阅所有三个领域的题目,因多重编码设计分组为阅读1、2和数学1、2、3以及科学。
三、评分者效应分析及结果
(一)分析程序
分别使用两个模型加以分析:(1)无评分者效应模型;(2)评分者效应模型。所有分析都在ConQuest软件中完成[12]29-55。PISA试题册中分别有(0,1)记分和(0,1,2)记分的题目,适用分步记分(partial credit)的多侧面Rasch模型。无评分者效应模型即在多侧面Rasch模型中去掉评分者效应参数Cj,对PISA数据来说,该模型即简化为Rasch家族模型中的分步记分模型。
(二)分析结果
1.模型比较
表2和表3分别为阅读、数学和科学三个领域无评分者效应模型和评分者效应模型的比较结果。
表2显示,对阅读1和科学来说,与无评分者效应模型相比,评分者效应模型拟合的更好(p值分别为0.000 7和0.022 3);对阅读2来说,无评分者效应模型与评分者效应模型没有显著差异(p=0.254 5)。这说明阅读1和科学试题上存在显著的评分者效应,但阅读2的题目上则无评分者效应。表3说明,数学2上有显著的评分者效应(p=0.024 8),而数学1和数学3上则无评分者效应(p值分别为0.543 5和0.859 0)。换句话说,分别评阅阅读2、数学1和数学3的4个评分者在使用相应的评分指南时较为一致,而评阅阅读1、科学和数学2的评分者在使用评分指南时差异较大。下面仅以阅读1的结果展示评分者效应模型的分析。

表2 阅读和科学无评分者效应模型和评分者效应模型的比较结果表

表3 数学无评分者效应模型和评分者效应模型的比较结果表
2.阅读1的评分者效应
(1)评分者的严苛度/宽松度。图1是表征阅读1子领域上考生能力、题目难度和评分者效应大小的怀特图(Wright Map)。表4呈现了18个评分者严苛度/宽松度的估计值(按照从宽松到严苛的顺序排列)和相应的标准误。可以看出,评分者间的严苛度/宽松度存在显著的差异。评分者严苛度/宽松度估计值间的最大差异(即估计值的最大值与最小值之差)为0.854个逻辑单位(logit),这个值接近考生能力测量分布全域的五分之一。换句话说,如果与考生潜在能力分布的标准差0.640相比,差异值0.854则意味着,如果忽略评分者严苛度/宽松度的影响,那么某个学生的能力估计值将在潜在能力分布上移动多于一个标准差的位置。因此,为取得较高的评分者一致性,尽管之前有严格的培训环节和质量监控,但是对阅读1上的评分者严苛度/宽松度的测量仍然呈现异质性。这一异质性也被怀特图下方的分离统计量(separation statistics)所验证:(1)卡方检验的值非常显著,表明至少有两个评分者的严苛度/宽松度估计值并不相同(在允许测量误差的情况下);(2)评分者分离的信度(reliability of rater separation)也说明评分者在编码指南的使用上非常不一致。

图1 阅读1的怀特图
如果使用评分者严苛度/宽松度估计值的均值作为比较的标准[13],那么则有5名评分者(28%)的严苛度/宽松度显著地低于均值,即这些评分者在评分过程中表现得较为宽松;同样地,也有5名评分者(28%)的严苛度/宽松度显著地高于均值,即这些评分者在评分过程中表现得较为严苛。图2显示了评分者参数估计值的位置,按照最宽松到最严苛的评分者进行排列,每个评分者严苛度/宽松度估计值伴随着相应的95%的置信区间。该图表明,如果评分者的95%的置信区间与均值交叉,那么该评分者与均值无显著差异;否则,则存在显著差异。需要注意的是,评分者743的95%置信区间最长,该评分者在ConQuest估计中处于最后一个位置,默认为被限制(constrain)的参数,这是程序规则造成其有如此大的标准误的原因。
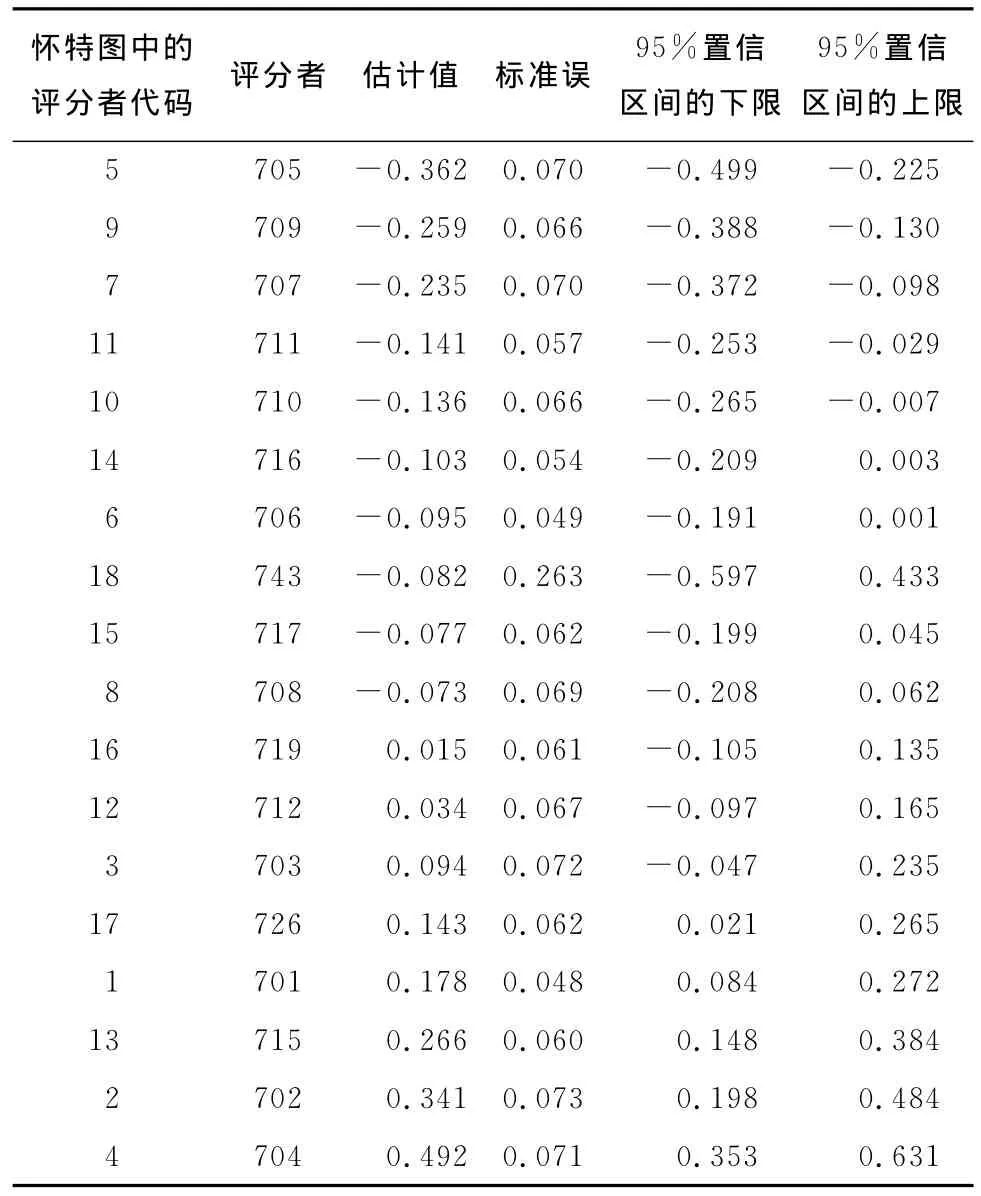
表4 阅读1评分者的严苛度/宽松度表

图2 阅读1评分者严苛度/宽松度估计值和95%的置信区间图
(2)评分者拟合(rater fit)。评分者拟合指在对考生的作答进行评分时,评分者自身在使用编码指南时的一致性程度。ConQuest为每个评分者提供了两类均方统计量以表征数据——模型拟合程度,即评分者加权和未加权的拟合统计量。其中,加权拟合统计量对评分者累积后的不一致评分较为敏感,而未加权的拟合统计量则对评分者单个的不一致评分较为敏感。这两个统计量的期望值均为1,其值域范围为0至无穷大[4,14]。
如果某个评分者的拟合统计量大于1,则说明该评分者的评分比模型期望的评分显示出更大的变异;由这类评分者提供的数据倾向于不拟合(misfit)模型。相反地,如果某个评分者的拟合统计量小于1,则说明该评分者的评分比模型预期的评分显示出较小的变异;由这类评分者提供的数据则倾向于过分拟合(overfit)模型。作为一种经验法则,Linacre建议加权和未加权的均方统计量均以0.50和1.50作为其控制下限和控制上限[14],也有研究者建议使用较窄的控制范围,即0.70(或0.75)到1.30[8]122-150[15]201-203。
18个评分者的加权和未加权统计量按照未加权统计量的值加以排序的结果见表5。加权和未加权统计量的排序非常相似。结果显示,评分者的拟合统计量均大于1,在使用较宽松的拟合统计量标准即0.50~1.50时,仅有7个评分者(39%)的拟合统计量的值处在可接受的范围内,然而却有11个评分者(61%)的拟合统计量属于不拟合的类别。因此,在很大程度上,该结果说明评分者在评分过程中体现出内部不一致性,且没有恰当地使用编码指南。

表5 阅读1的评分者拟合统计量表
四、结论与讨论
本研究的主要目的是考察PISA 2009中国试测研究在阅读、数学和科学三个领域的评分工作中是否存在显著的评分者效应。结果显示,PISA 2009中国试测研究的评分者效应分析的结果在三个领域上不一致。将阅读分为两个部分加以分析后,阅读1的18个评分者在严苛度/宽松度上存在显著的差异;阅读2的4个评分者则显示其较为一致地使用了编码指南。数学被分为三个部分加以分析后,数学2的4个评分者在严苛度/宽松度上有较少的差异,只有一名评分者(727)的严苛度/宽松度显著地高于均值0;而数学1和数学3没有显著的评分者效应。科学中的9个评分者在评阅考生的反应时存在非常显著的评分者严苛度/宽松度效应。
本研究认为PISA 2009中国试测研究在阅读、数学和科学均存在评分者效应。该结论与语言测验领域和成就测试领域中的一些相关研究的结论是一致的[16]261-287。同时,本研究发现如果评分者之间的严苛度或宽松度差异较大,将导致相当一部分考生的真实能力水平被低估(当评分者较为严苛时)或被高估(当评分者较为宽松时)。这个发现显示,如果在事关考生个人利益的高风险考试中不考虑评分者效应,那么对考生来说是不公平的,为降低评分者效应对考生能力估计的影响,多侧面Rasch分析能为每个考生产生一个期望的评分值[17],这个评分来自于一个假设的评分者,该评分者的严苛度或宽松度水平为0,即均值水平。这个“公平均值(fair average)或公平分数(fair score)”能提供一个与评分者无关的考生能力估计值。此外,根据分析结果,阅读1和科学的绝大多数评分者的拟合统计量均属于不拟合的类别,说明评分者展现出的差异比模型所预期的变异更大。换句话说,这些评分者自身不能一致地使用编码指南。一个可能的原因是有一些评分者被要求评阅所有三个领域的题目。可以想象,跨领域培训会给评分者造成了较大的认知负担。另外,评分过程中不可避免地会出现疲劳效应以及对每个领域编码指南的理解程度的不同。通过比较这两个研究的结果可以发现,在今后的评分设计中,我们推荐从有经验的教师和学科专家中选取评分者,并针对不同的领域设计适当的评分程序。在今后的研究中,我们将根据本分析得到的参数估计值作为真值,进行模拟研究,以比较实证分析与模拟分析的结果,为研究结果提供更多支持性证据。
现在以高考为背景讨论一下所获得的研究结论在高考中可能的应用前景。
与PISA相比,高考开放题的比重大大增加,更为重要的,与PISA开放题大部分评分设计被限制在(0,1)和(0,1,2)记分不同,高考各学科很多开放题目的满分达12至15之多,更不要说作文的满分要高达60分。一份48分的作文和一份44分的作文究竟能在多大程度上显示出差别?是什么样的人在评分?有哪些质量控制程序?一道开放题的满分以多少为合适?扣分和得分的依据和标准是什么?凡此种种,如果不能有效地控制评分者之间和评分者自己在不同时间不同场合下评分的差异和不稳定性,评分结果的误差就有极大的可能掩盖原本精心设计的题目的考查功能。
中国绝大多数省的高考已经实现网上阅卷,但目前网上阅卷的组织形式更多地只是把人工阅卷积累起来的丰富经验和计算机技术有机结合,从而提高工作效率。事实上,网上阅卷更大的意义是它使得在传统的阅卷组织形式下绝无可能的一种全新的业务创新成为可能。在网上阅卷中,计算机系统可以将考生和阅卷员的各种个人信息、答题信息和阅卷信息的海量资料全部详细存储起来并加以实时处理,这就为应用教育测量理论和各种较新的统计方法来提高阅卷质量、控制评分误差提供了可能。从理论上说,完全可以结合网上阅卷的管理流程,应用现代测量评价技术和方法,提高评分的信度和效度,这才是网上阅卷的根本价值所在。按此思路,至少以下一些方向是值得管理部门和研究人员思考和改进的:为主观题评分确定客观公正的评分标准和程序,建立并应用评分者质量指标去挑选和管理高水平的评分队伍,将较为关键和重要的题目分派给较高水平的评分者,实时监测和调整评分者效应,及时发现抄袭和雷同等作弊现象并加以惩罚,及时发现有创见有新意的答案并给予奖励,最大限度地消除评分者效应。PISA中国试测研究的实践证明这是完全可能的,比如,PISA评分者效应模型中获得的考生能力已经是综合考虑了评分人员严苛度差异自动调节后的结果。
[1] Scullen S E,Mount M K,Goff M.Understanding the Latent Structure of Job Performance Ratings[J].Journal ofApplied Pyschology,2000,85(6).
[2] Messick S.Validity of Psychological Assessment:Validation of Inferences from Persons’Responses and Performances as Scientific Inquiry into Score Meaning[J].American Psychologist,1995,50(9).
[3] Weir C J.Language Testing and Validation:An Evidence-Based Approach[M].Houndmills,England:Palgrave Macmillan Press,2005.
[4] Myford C M,Wolfe E W.Detecting and Measuring Rater Effects Using Many-Facet Rasch Measurement:Part I[J].Journal of Applied Measurement,2003,4(4).
[5] Lunz M E,Wright B D,Linacre J M.Measuring the Impact of Judge Severity on Examination Scores[J].Applied Measurement in Education,1990,3(4).
[6] 吴志明,张厚粲.结构化面试中的评分一致性问题初探[J].应用心理学,1997,3(2).
[7] 苏永华.国家公务员录用面试初步分析[J].应用心理学,1998,4(1).
[8] Wilson M.Constructing Measures:An Item Response Modeling Approach[M].Mahwah,NJ:Lawrence Erlbaum Associates Publishers,2005.
[9] Linacre J M.Many-facet Rasch Measurement[M].Chicago,IL:MESA Press,1994.
[10]田清源.HSK主观考试评分的Rasch实验分析[J].心理学探新,2007,27(1).
[11]OECD.PISA 2009Results:What Students Know and Can Do-Student Performance in Reading,Mathematics and Science(Volume I)[M].Paris:OECD Publishing,2010.
[12]Wu,Adams,Wilson,et al.ACER ConQuest Version 2.0:Generalized Item Response Modeling Software[M].Melbourne:ACER Press,2007.
[13]Wolfe E W.Identifying Rater Effects Using Latent Trait Models[J].Psychology Science,2004,46(1).
[14]Linacre J M.What Do Infit and Outfit,Mean-Square and Standardized Mean?[J].Rasch Measurement Transactions,2002,16(2).
[15]Bond T G,Fox C M.Applying the Rasch Model:Fundamental Measurement in the Human Sciences[M].Mahwah,NJ:Lawrence Erlbaum Associates Press,2001.
[16]Engelhard G Jr.Monitoring Raters in Performance Assessments[C]//Tindal G,Haladyna T M.Large-scale Assessment Programs for All Students:Validity,Technical Adequacy,and Implementation.Mahwah,NJ:Lawrence Erlbaum Associates Press,2002.
[17]Eckes T.Examining Rater Effects in TestDaF Writing and Speaking Performance Assessments:A Many-Facet Rasch Analysis[J].Language Assessment Quarterly,2005,2(3).
PISA China Trial Rater Effects Analysis for Gaokao Online Rating
WANG Lei1,ZHANG Wen-jing2
(1.National Education Examinations Authority,The Ministry of Education,Beijing 100084,China;2.Institute of Developmental Psychology,Beijing Normal University,Beijing 100875,China)
The aim of this study was to analyze rater effects in reading,math,and science for PISA2009China Trial Study.Based on the many-facet Rasch measurement methodology,the focus was on the rater main effects in the three subjects respectively.Results show that considerably strong rater severity/leniency effects occurred in reading and science,but a relatively weak rater severity/leniency effects for math.The potential reasons about these results were discussed and some implications for National College Entrance Examination(commonly referred to as“Gaokao”))online ratings are provided.
rater effects;severity/leniency;PISA;multiple coding;online rating of Gaokao
book=95,ebook=5
B841
A
1007-3116(2012)06-0095-07
(责任编辑:王南丰)
2012-01-20
全国教育科学规划2009年度教育考试研究专项课题《学生能力国际评价PISA的教育评价技术在高考中的应用》(GFA097021)
王 蕾,女,北京人,管理学博士,副研究员,研究方向:教育管理与评价;张文静,女,山东枣庄人,博士生,研究方向:心理测量与评价。
