重卡外气动性能评估与优化

唐克兵，赵禧元，谢庆喜，赵曜

（东风汽车有限公司 东风商用车技术中心，武汉 430056）

节能、安全与排放是当今汽车工业的三大课题，而汽车空气动力学特性与这三大课题紧密相关。汽车空气动力学特性直接影响着汽车的动力性、燃油经济性、操纵稳定性、舒适性和安全性，因此，汽车空气动力学特性已成为评价汽车造型优劣的重要依据。

空气动力学的研究主要有两种方法：第一、进行风洞试验；第二、通过CFD软件进行数值模拟。风洞试验能够得到具有较高可靠性的结果，但是它也有诸如成本高、周期长等局限性，而这显然不能适应不断变化的市场需求。随着计算机技术的迅猛发展，通过CFD软件进行数值模拟由于其计算精度接近风洞试验，而又大大缩短了设计周期的优点，从而被广泛的应用。

本文论述了用格子—玻尔兹曼方法（LBM）计算整个卡车的外流场特性。这种方法允许保留所有的几何细节包括最小的元件如管子和电线。几何可以包括外部和内部的部件。表面/气流的相互作用和自动格子生成方法可以使仿真准备时间大大缩短。同时，该方法高数值效率允许使用大规模的单元，因此会有较高精度的结果。本文仿真计算是采用商业LBM算法软件PowerFLOW来进行的。

1 数学模型

流体仿真一个主要的困难就是难以足够离散化流体区域，同时解析复杂几何的表面细节。在工业应用上最多的纳维—斯托克斯方法对实际计算的网格质量和尺寸要求较高。这些要求是有限体积法特性的直接要求，有限体积法是 N-S方程数值求解采用最多的方法。该方法利用压力修正运算法则来保持质量守恒。压力修正是一个数值庞大的交互过程，因此限制了用来实际计算的有效网格尺寸。为了限制单元数量，一般采用非结构化网格，可以离散复杂几何同时保持较少的单元数。非结构化网格形状的变化导致结果不可避免的依靠网格尺寸和质量。在过去这些年N-S方程求解的网格产生法则已经有所提高而且相当多的过程是自动的。然而，几何表面的准备和许多网格生成程序仍然需要用户参与。这部分工作量仍然很大，而且比较强的依赖于网格划分者的技能。全部划分网格过程限制几何细节的水平，在实际使用和大多数项目中，需简化几何以降低准备时间，保证产品设计节点。

格子—玻尔兹曼方程（LBE）求解是维纳—斯托克斯求解的一个替代。它们不需要任何特别的交互程序且能实现质量、动量和能量守恒。因而，LBE求解在数值上非常有效且稳健。增加的数值效率允许操作数量非常大的单元（或voxels）。另外，玻尔兹曼方程的特性提高了流体与壁面的相互作用。表面单元（或者surfels）用来设计作为有效单元与相邻格子单元交互作用。大量的格子和动态表面处理的组合允许不需几何简化就精确的表示曲面。

2 格子—玻尔兹曼方程的原理

玻尔兹曼方程可以写成下述的形式：

其中f为速度分布函数，Θ为碰撞算子。玻尔兹曼方程的格子形式可以表达为各个状态下的可能分布的一列代数方程：

其中碰撞算子用BGK形式［1］建模：

平衡分布函数 fi（0）为速度的扩展［1］：

可以表明玻尔兹曼方程不再屈从于N-S方程。更精确的说，N-S方程代表玻尔兹曼方程在小Knudsen数上的子集。玻尔兹曼方程求解一个好的特征是通过执行所有状况下的碰撞都等于零来自动实现质量和动量守恒的：

湍流影响采用以原来的RNG公式［2，3］为基础的修正的k-ε模型建模：

无量纲系数的值与起初模型的公式［2，3］中的值相同。以LBE为基础的湍流波动描述包含流动过程和回流信息，包括高阶项来解雷诺压力的非线性［4］。这与趋向于使用以雷诺压力模型为基础的常规线性涡流黏性典型的N-S求解截然不同。

3 仿真计算及改进

3.1 仿真模型

建立了详细的整车模型，包括车身、外饰件、车架、底盘（包括了发动机、变速箱和冷却系统）、前轮、油箱等。整车模型如图1。

3.2 计算边界条件

计算边界条件见表1

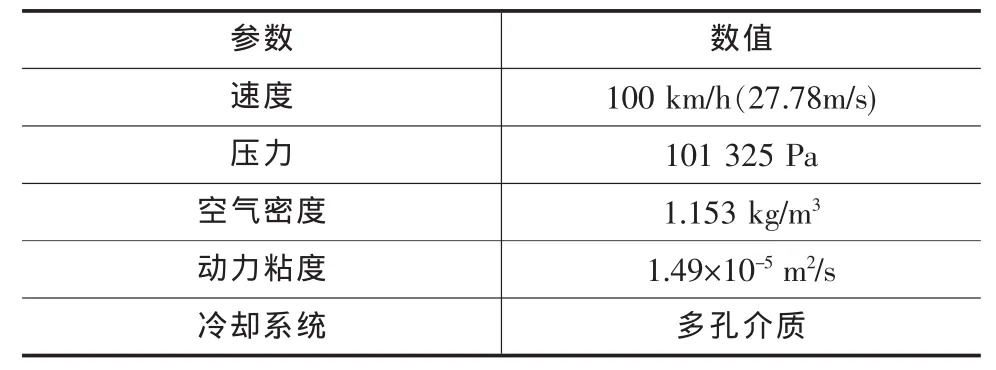
表1 计算边界条件

3.3 计算结果及分析

经过迭代计算后，得到流场结果，压力分布如图2～图6所示。

从图2整车表面压力云图可以看出，车身正面、遮阳罩、后视镜，货箱正面均出现高压力区，这些高压区的产生将导致整车风阻的增加。

从图3可见，后视镜存在过大的压力滞止区，而且使得过多的气流从后视镜外侧流过，可以通过改进后视镜的结构减小压力滞止区和后视镜尾流的大小。

图4为遮阳罩局部的压力云图，可见由于台阶和正面高压冲击的影响，遮阳罩附近存在明显的流动分离，可以优化遮阳罩的形状来避免高压冲击和边角流动分离，更改台阶的形状来减少台阶下游的流动分离。

图5为货箱正面的静压云图，可见由于流动气体直接冲击货箱的上边角产生了流动分离，这可以通过优化顶部导流罩角度、长度和半径来减小流动滞止区。后扰流板的后缘边角导致货箱边角出现较大的流动滞止。

图6是货箱侧面的静压云图，可见货箱侧边的流动滞止区只有很小的压力增加。此处不是必须要进行优化的，但在后视镜尾流减小，并且更改顶部导流罩之后侧边的流动滞止区可能会增大。

3.4 结构改进及效果对比

通过以上的分析，结合实际情况，对顶导流罩结构部分曲面的曲率进行调整，改型后整车风阻相比改型前下降7.4%。

从图7可以看到，改型后车身与货箱间的流速明显下降，相应的空气动能大为降低，而图8显示，货箱前部顶端部分压力同样明显下降。

从图9可以看出，改型后货箱正面高压区明显减少，这也是导致风阻系数降低的主要原因。

4 结论

应用数字仿真方法对某款重卡进行外流场分析，得到整车表面的压力分布、流场速度、整车的风阻系数等重要气动参数。根据流场特性，对局部区域的结构进行改进，改型后整车风阻，系数降低7.4%，事实证明应用数字方法进行整车气动特性分析与改型，对降低开发成本，缩短开发周期，减小风阻降低用户后续使用费用，进而提高产品综合竞争力具有重要意义。

［1］D.d’Humieres，P.Lallemand and Y.H.Quian.Lattice BGK models for Navier-Stokes equations［J］.，Europhysics Letters17（6）：479-484，1992.

［2］V.Yakhot，and S.A.，Orszag.Renormalization Group Anal ysis of Turbulence.I.Basic Theory ［J］.J.Sci.Comput 1（2），3-51，1986.

［3］V.Yakhot，V.，S.A.Orszag，S.Thangam，T.Gatski，and C.Speziale.Development of turbulence models for shear flows by a double expansion technique ［J］.Phys.Fluids A 4（7），1510-1520，1992.

［4］H.Chen，S.A.Orszag，I.Staroselsky，and S.Succi.Expanded Analogy between Boltzmann Kinetic Theory of Fluid and Turbulence［J］.J.Fluid Mech 519：307-314，2004.