基于SVM的厚松散层矿区开采下沉系数预测模型

韩奎峰，康建荣

(1.中国矿业大学环境与测绘学院，江苏徐州221116;2.徐州师范大学测绘学院，江苏徐州221116)

基础研究

基于SVM的厚松散层矿区开采下沉系数预测模型

韩奎峰1，2，康建荣2

(1.中国矿业大学环境与测绘学院，江苏徐州221116;2.徐州师范大学测绘学院，江苏徐州221116)

针对厚松散层薄基岩矿区开采沉陷变形预计中存在的下沉系数偏大问题，以23个开采工作面的地质采矿条件及其下沉系数为学习和测试样本，将文化－随机粒子群算法 (CA－rPSO)和支持向量机 (SVM)相结合，利用CA－rPSO的快速并行寻优功能优化SVM参数，建立了厚松散层薄基岩开采条件下下沉系数的SVM预测模型。通过实例验证SVM的预计结果与实际符合较好。

SVM;厚松散层;下沉系数

厚松散层矿区通常是“三下”采煤问题突出的地区，根据相关研究结果［1－6］，在厚松散层矿区用概率积分法预计可以取得满意的预测精度。通过对多个厚松散层矿区和具有相同基岩薄松散层矿区观测站所求得的概率积分法参数对比，发现厚松散层矿区的下沉系数明显偏大，其他参数变化不明显。厚松散层矿区采煤工作面的地质采矿条件和下沉系数之间存在复杂的非线性关系［5］。基于支持向量机 (SVM)的算法适宜处理复杂的非线性关系［7－12］，具有良好的推广性能。因此分析厚松散层矿区影响下沉系数的主要因素，建立基于SVM的下沉系数预测模型，具有重要的现实意义。

1 淮南新矿区和皖北矿区概况

淮南新矿区和皖北矿区均属典型的厚冲积层矿区，淮南老矿区属薄松散层矿区。淮南新矿区的潘集区松散层厚度为120～360m，谢桥、张集区松散层厚度为194～485 m。皖北矿区松散层厚度则为30～375 m。

为研究由采煤引起的地表移动变形规律，在淮南新矿区和皖北矿区建立了地表移动观测站，淮南新矿区的3个矿区共布设12个观测站，其中潘集区5个，谢桥区3个，张集区4个;皖北矿区共设有18个观测站:刘桥二矿、毛郢孜矿和祁东矿各1个，任楼矿9个，百善矿和刘桥一矿各3个。淮南老矿区共设有10个观测站:李咀孜矿和新庄孜矿各2个，李一矿和谢二矿各1个，谢一矿4个。各矿区从首采开始陆续开展了观测站的观测工作，得到了大量的地表移动变形数据，为厚松散层矿区的开采沉陷规律研究提供了可靠的数据基础。

2 概率积分法预计参数及影响下沉系数的主要地质采矿因素分析

为了解概率积分法预计参数在厚松散层和薄松散层矿区有何不同，将每个观测站计算得到的概率积分法预计参数进行归纳分析［3］，将分析结果列入表1中。

表1 概率积分法预计参数分析

由表1可知，厚松散层矿区的下沉系数q明显偏大，水平移动系数b，主要影响角正切tgβ以及拐点偏移距s则变化不大，下沉系数大小与松散层厚度具有明显的相关性，但地下采煤引起地表移动变形是一个复杂的过程，仅研究松散层厚度和下沉系数的关系显然不妥，要准确掌握厚松散层矿区下沉系数的变化规律，应该全面分析影响下沉系数的地质采矿条件。

相关文献显示［2，5－6，10，14］，影响下沉系数的因素有:覆岩岩性、煤层倾角、深厚比、松散层厚度、采动程度、采动次数、采煤方法和顶板管理方法等。根据煤田地质勘探资料，淮南矿新区和皖北矿区基岩岩性属软岩性，且具有一致性;从观测站资料可知，工作面很少采用分层开采的方法，只有5个观测站属重复开采情况，数据量小，难以找到重复开采的地表移动变形规律;顶板管理方法均采用全部垮落法;采煤方法均为走向长壁采煤法。剔除相同的地质采矿影响因素，将松散层厚度、煤层倾角、采厚、采动程度和采深5个因素作为SVM算法学习训练样本的因子指标。

3 SVM的厚松散层矿区下沉系数预测模型

3.1 SVM原理

SVM是实现了统计学习理论中结构风险最小化原则的实用算法，由Vapnik等学者首先提出，比较成功地解决了模式分类问题。考虑一组独立同分布分训练样本 {(xi，yi)|xi∈Rn，yi∈R，i= 1，2，…，l}，SVM回归建模是通过内积函数定义的非线性变换将输入空间变换高维特征空间(Hilbert空间)，并在这个空间进行线性回归［7，9，12］。线性函数表示为:

式中，为Rn→H;ω和b为权值系数和偏置量。根据结构风险最小化原则，函数回归问题等价于以下泛函最小［10］:

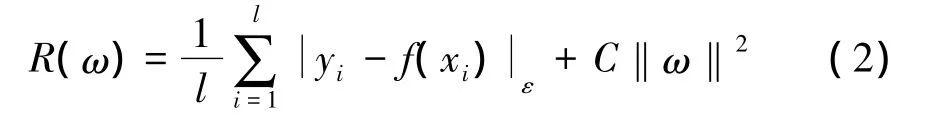
式中，C＞0，表示超出误差ε的惩罚程度。

利用Lagrange乘子法，根据对偶定理和Karush-Kuhn-Tucker(KKT)条件，得到对应的对偶问题:

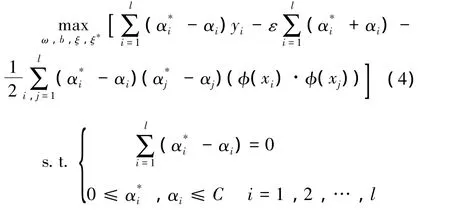
解上述凸二次规划问题得到非线性映射:

根据Mercer定理定义的内积核:

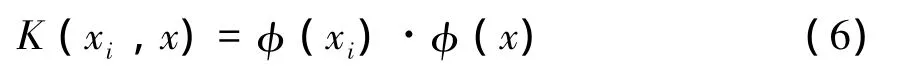
得到SVM拟合函数:

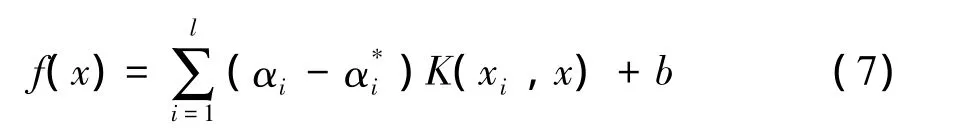
其中，K(xi，x)为满足Mercer条件的对称函数，称为核函数，文中选择径向基 (RBF)核函数K(xi，xj)=exp(－γ║xi－xj║2)。

3.2 学习训练和验证测试样本数据的选择

要获得高精度的基于SVM的预测模型，足够多、质量高的学习训练样本数据是根本保障，从淮南矿新区和皖北矿区的观测站数据来看，可以建成一个很好的学习训练样本。经过整理、分析将样本数据列入表2中。样本中“采动程度”是根据经验公式来计算［1］。表2中，序号为1～20，21～23的样本为验证测试样本。

3.3 支持向量机预测模型建立及精度评价

SVM的学习性能和泛化能力主要取决于核函数及其宽度系数、惩罚因子以及不敏感损失系数等参数的选择，一般通过交叉验证试算的方法，盲目且耗时，难以获得最佳逼近效果。本文选用径向基函数 (RBF)作为核函数，并根据实际下沉系数的计算精度要求，将最终结果容许误差取为0.001，以1～20为建模样本，采用文化－随机粒子群算法(CA－rPSO)，按“留一法”优化SVM参数。通过反复实验，最终得到计算下沉系数的最佳SVM参数 (C，σ)为 (128.71，0.001)，并建立了厚松散层下沉系数SVM的预测模型。图1为模型预计值与实测值的对比图，从图1可以直观地看出预计值和实测值拟合程度较高。为更全面了解所建模型的精度，采用模型计算的中误差 (MSE，Mean Square Error)和平均绝对误差百分率 (MAPE，Mean Absolute Percentage Error)对模型的预测精度进行评价。MSE和MAPE分别用式 (8)和式(9)进行计算。

表2 学习训练及测试样本

图1 预计值和实测值对比

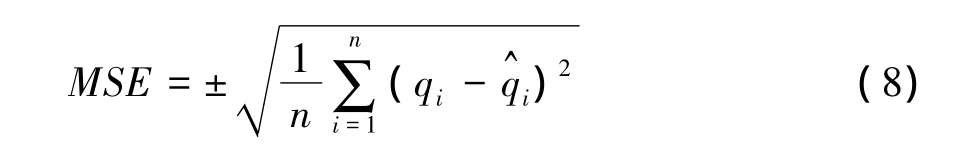
式中，qi分别是下沉系数的实测值和预计值，n为训练样本总数，取值20。另外，泛化性能是衡量一个预测模型的重要指标，本文利用威尔莫特一致性指数 (WIA，Willmott’s Index of Agreement)来考察所建模型的泛化性能［9］，一般认为，WIA值大于0.6，模型才具有实际意义。WIA采用式(10)来计算。

式中，qi，和n含义同上文，。经计算，得到MSE=0.02，MAPE=0.37，WIA=0.91。从计算结果看，该模型具有较好的拟合性能，精度较高，泛化能力强。

3.4 模型测试结果

采用21～23号样本数据对建立的模型进行测试，将计算结果和预计结果列入表3。

表3 SVM预测精度

由表3可知，下沉系数最大绝对误差均小于3倍中误差，测试结果表明，基于SVM建立的厚松散层矿区下沉系数计算模型准确、可靠。在工作面地质采矿条件明确的前提下，该模型可以得到满足现场精度要求的下沉系数值。

4 结论

(1)通过对厚松散层矿区和具有相同基岩薄松散层矿区实测概率积分法预计参数的对比分析，发现厚松散层矿区的下沉系数明显偏大，其他参数变化不明显。

(2)在综合分析影响厚松散层矿区下沉系数因素的基础上，建立了基于SVM的厚松散层矿区下沉系数计算模型。分析结果表明，模型具有较好的拟合性能，精度较高，泛化能力强。利用多个实测样本对模型进行测试，所得下沉系数值在允许误差范围内，绝对误差小，能满足实际工作需要。

(3)基于SVM的厚松散层矿区的下沉系数计算模型综合考虑了影响下沉系数的主要地质采矿因素，为没有观测站的类似矿区提供了一种计算下沉系数的新方法，其他预计参数可以类比具有相同基岩的薄松散层矿区的参数，有较高的实用价值。

［1］中华人民共和国国家煤炭工业局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程［M］.北京:煤炭工业出版社，2000.

［2］高荣久，胡振琪，谢宏全，戚家忠.特厚冲积层非主断面观测站岩移参数的求取［J］.辽宁工程技术大学学报，2006，25(3):332－335.

［3］米丽倩，查剑锋，刘丙方.概率积分法参数对预计地表下沉的影响度分析［J］.煤矿开采，2011，16(4):13－16.

［4］郭文兵，邓喀中，邹友峰.概率积分法预计参数选取的神经网络模型［J］.中国矿业大学学报，2004，33(3).

［5］余华中，李德海，李明金.厚松散层放顶煤开采条件下地表移动参数研究［J］.焦作工学院学报 (自然科学版)，2003， 22(6):413－416.

［6］王金庄，常占强，陈 勇.厚松散层条件下开采程度及地表下沉模式的研究［J］.煤炭学报，2003，28(3):230－234.

［7］蒋爱武，谢寿生.基于支持向量机和粒子群算法的压气机特性计算［J］.航空动力学报，2010，25(11):2571－2577.

［8］李永树，王金庄，陈 勇.开采沉陷地区下沉系数分析［J］.矿业研究与开发，1998，18(2):1－7.

［9］李培现，谭志祥，闫丽丽，等.基于支持向量机的概率积分法参数计算方法［J］.煤炭学报，2010，35(8).

［10］张宏贞，邓喀中，刘洪义.老采空区残余下沉系数的神经网络模型研究［J］.采矿与安全工程学报，2009，26(3).

［11］郭文兵，邓喀中，邹友峰.条带开采下沉系数计算与优化设计的神经网络模型 ［J］.中国安全科学学报，2006，16 (6):40－45.

［12］于宁锋，杨化超，邓喀中，等.基于PSO和SVM的矿区地表下沉系数预测［J］.辽宁工程技术大学学报 (自然科学版)，2008，27(3):365－367.

［13］郭文兵，邓喀中，邹友峰.地表下沉系数计算的人工神经网络方法研究［J］.岩土工程学报，2003，25(2):212－215.

［14］邹友峰.地表下沉系数计算方法研究［J］.岩土工程学报，1997，19(3):109－112.

［责任编辑:张玉军］

Prediction Model of Subsidence Ratio Coefficient for Mining under Thick Loose Bed Based on SVM

HAN Kui-feng1，2，KANG Jian-rong2

(1.Environment＆Surveying School，China University of Mining＆Technology，Xuzhou 221116，China; 2.Surveying School，Xuzhou Normal University，Xuzhou 221116，China)

In order to resolve the problem that subsidence coefficient is too large in predicting subsidence and deformation when mining under thick loose bed and thin bed rock，taking the geological and mining conditions and subsidence coefficients from 23 mining faces，combining culture－random particle swarm optimization with SVM so as to optimize SVM parameters with fast parallel optimizing function，SVM subsidence coefficient prediction model for mining under thick loose bed and thin bed rock was set up.Examples showed that prediction value well met actual result.

SVM;thick loose layer;subsidence coefficient

TD325.2

A

1006-6225(2012)04-0008-03

2012－04－12

国家自然科学基金项目:山西煤矿开采引起的高陡边坡失稳机理研究 (51074139)

韩奎峰 (1975－)男，山东夏津人，博士研究生，讲师，现从事开采沉陷方面的教学和研究工作。