Risk Measure and Premium Distribution on Catastrophe Reinsurance∗

XUN LIAND WANG DE-HUI

(1.Institute of Mathematics,Jilin University,Changchun,130012) (2.Basic Science School,Changchun University of Technology,Changchun,130012)

Risk Measure and Premium Distribution on Catastrophe Reinsurance∗

XUN LI1,2AND WANG DE-HUI1

(1.Institute of Mathematics,Jilin University,Changchun,130012) (2.Basic Science School,Changchun University of Technology,Changchun,130012)

In this paper,we propose a new risk measure which is based on the Orlicz premium principle to characterize catastrophe risk premium.The intention is to develop a formulation strategy for Catastrophe Fund.The logarithm equivalent form of reinsurance premium is regarded as the retention of reinsurer,and the di ff erential earnings between the reinsurance premium and the reinsurer’s retention is accumulated as a part of Catastrophe Fund.We demonstrate that the aforementioned risk measure has some good properties,which are further con fi rmed by numerical simulations in R environment.

catastrophe reinsurance,catastrophe fund,Orlicz premium principle, Haezendonck-Goovaerts risk measure,stochastic ordering

Stop-loss reinsurance is the optimal contract in many cases(see,e.g.,[7–8]).We use a new risk measure based on the Orlicz premium principle(see[9–10])to determine the stop-loss reinsurance premium and then to propose a premium distribution scheme.

The new risk measure has some good properties such as monotone,translation invariance,convex-preserving,subadditivity and upper and lower boundedness,which are further con fi rmed by numerical simulations.Some concepts of stochastic order can be found in [11–14].

The rest of this paper is orgnalized as follows:in Section 2,we present the de fi nition and some properties of the new risk measure.Section 3 compares the new risk measure with Haezendonck-Goovaerts risk measure and suggests the premium distribution scheme. Sections 4 describes the numerical simulation results.Section 5 gives the conclusions,and fi nally,Appendix contains some proofs.

2 A New Risk Measure Based on the Orlicz Premium Principle

For given risk variable X∈L∞and α∈[0,1),the Orlicz premium principle is given by the

+ unique solution Hα(X)of the equation

where φ(·)is a non-negative,strictly increasing,and continuous function on[0,+∞)withIn[15]the functional φ is described in detail,and in [16]we know that the φ is a convex function.

Denote by π an Orlicz risk measure on stop-loss reinsurance and x a retention.The

equation of Orlicz premium is

We modify the equation as

Let X be a continuous type random variable with the distribution function F(x),−∞≤be the α quantile of the risk X.represents the modi fi ed Orlicz risk measure of the risk X for the retention x at the level α.Then we have the following Theorem 2.1:

Theorem 2.1Let x be the retention,X,α and φ(·)are as the aforementioned.Thenand α∈(0,1),the equation(2.1)has a unique solution πα[X,x]satisfying the inequalities

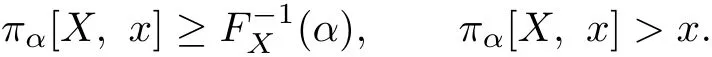
Proof. Let

It is clear that π＞x.

(1)For any π0

∈(x,+∞),from the Heine theorem and Levi theorem it follows that

Owing to the intermediate value theorem,the equation has a solution πα[X,x].

(2)H(π)is strictly monotonically decreasing,and the equation has a unique solution.

which is a contradiction.So

The proof is completed.

De fi nition 2.1Similar to the de fi nition of Haezendonck-Goovaerts risk measure(HRM), we call

the generalized Haezendonck-Goovaerts risk measure(GHRM)for the variable X,where πα[X,x]is the unique solution of the equation(2.1).

There are some properties about GHRM as the following theorems.

Theorem 2.2GHRM πα[X]satis fi es

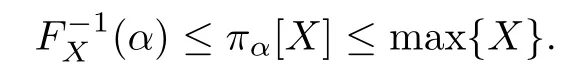
Proof. By Theorem 2.1,

Assume that

Then for any x,

By the proof of Theorem 2.1,H(π)is strictly monotonically decreasing,and φ is strictly monotonically increasing and continuous with φ(1)=1.FX(x)is continuous.Hence,there exists a δ＞0 such that for any|x−max{X}|＜δ one has

which is a contradiction.Therefore,

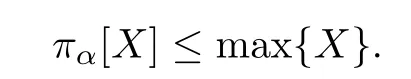
This proof is completed.

Remark 2.1(1) GHRM is(S,α)-consistent(see[10]),where S is a set of axioms for risk measures.

(2)π[X]=F−1(α)is the premium on percent principle of insurance and the probability

αXis the premium on maximum loss principle of insurance(see[17]).

Theorem 2.3Let φ satisfy Theorem 2.1,and α,0＜α＜1,be arbitrarily given.Then we have

(2)Translation Invariance:πα[X+a]=πα[X]+a for any a;

(3) Preservation of convex ordering:is convex,(for the=max{Y};

Proof. (1)Since X ≤stY,

is increasing,and

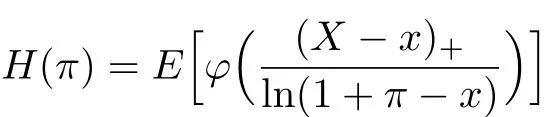
is decreasing,we have

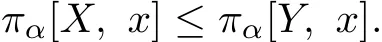
Thus

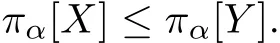
(2)By the unique solution of the equation

we have

Hence

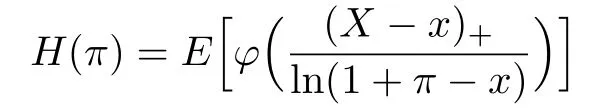
is strictly monotonically decreasing,we have

So

is derived.

(4)Firstly,we assume that

Since φ is an increasing convex function,we have

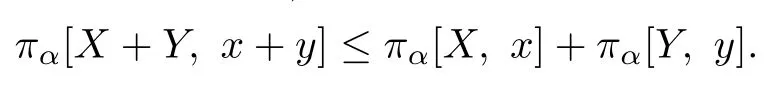
Hence

This ends the proof.

Theorem 2.4Let φi(i=1,2)be two non-negative,strictly increasing and continuous functions on[0,+∞)with

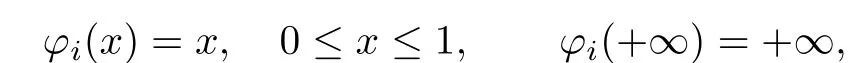
(1) If φ2is convex in φ1(see[10]),then

(2) If φ2is concave in φ1,then

According to the de fi nition that φ2is convex in φ1and the Jensen inequality,we get

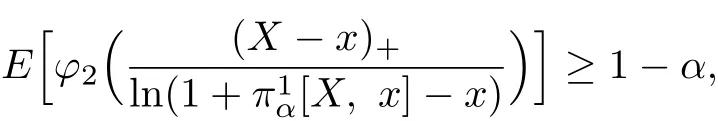
which contradicts the above conclusion.Then

Hence

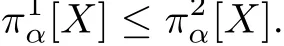
The proof is completed.

Corollary 2.1Let

Then

(1) πα[X]is the smallest GHRM on strictly increasing convex functions φ satisfying

(2) πα[X]is the largest GHRM on strictly increasing concave functions φ satisfying

Proof. It is clear th

is the solution of the equation(2.1)for φ(x)=x,which is strictly increasing on[F−1X(α), max{X}).Let φ1(x)=x.By Theorem 2.4,the corollary is proved.

3 Premium Distribution Scheme

For the function φ and the level α∈(0,1),denote HRM and GHRM as π0and π,respectively. The catastrophe insurance premium π is allocated as follows:x to insurer,ln(1+π−x)= π0

−x to reinsurer,and π−π0paid for Catastrophe Fund.

If the risk variable is light-tailed,then the risk is fully covered by insurance and reinsurance companies,the premium distributed to Fund closes to zero.Whereas the risk is heavy-tailed,the reinsurer has reasons to take out some premium to Catastrophe Fund as the reserves for huge damage with the magnitude of risk exposure increased.The insurer, reinsurer and Catastrophe Fund undertake the fi nancial losses due to insured catastrophic perils all together.

4 Numerical Simulations

In this section we study the numerical computation of πα[X]for

which are the same as[18].Given α=0.95 and the distribution of X,denoteas the simulation value ofand πα[X],respectively.Random sample of m=10000 values is generated severally from four types of distribution with the di ff erent parameters:Uniform(0,1),Uniform(0,2),Exponential(1),Pareto(4),Normal(0,1) and Normal(1,1),and repeat the procedure n=1000 times with the help of R.For these distributions above the true value of(X)and the simulation values ofπα[X]for φ1(x)=x are reported in Table 4.1

Table 4.1 Example of computations of.

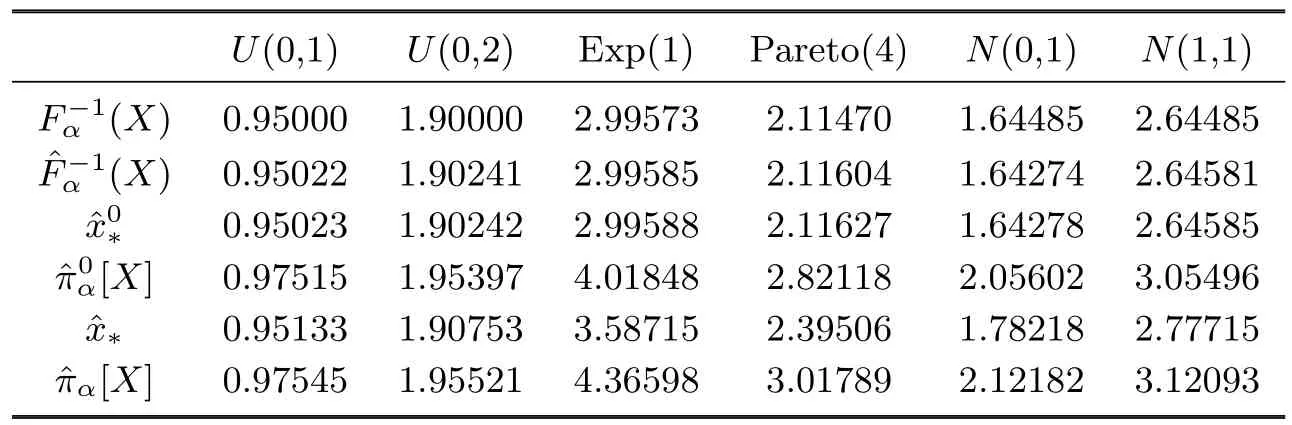
Table 4.1 Example of computations of.

U(0,1) U(0,2) Exp(1) Pareto(4) N(0,1) N(1,1) F−1 α (X) 0.95000 1.90000 2.99573 2.11470 1.64485 2.64485 ˆF−1 α (X) 0.95022 1.90241 2.99585 2.11604 1.64274 2.64581 ˆx0∗0.95023 1.90242 2.99588 2.11627 1.64278 2.64585 ˆπ0α[X] 0.97515 1.95397 4.01848 2.82118 2.05602 3.05496 ˆx∗ 0.95133 1.90753 3.58715 2.39506 1.78218 2.77715 ˆπα[X] 0.97545 1.95521 4.36598 3.01789 2.12182 3.12093

In Table 4.1,xˆ0∗andxˆ∗are simulation values of the theoretical minimum point correspondThe values ofalways grow from small to large

for the identical distribution,and the values ofFˆ−1(X)andxˆ∗are close to the theoretical

α0value ofX).Moreover,for X∼Uniform(0,1)and Y∼Uniform(0,2),one has

For Normal(0,1)and Normal(1,1),the conclusion of

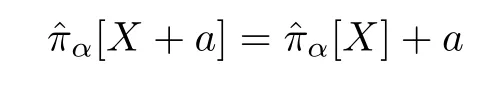
is drawn.

In Table 4.2,the conclusions for φ2(x)are similar to those in Table 4.1.

Table 4.2 Example of computations of

Fig.4.1 The functions and minimizations ofˆπα[X,x]

5 Conclusion

In this paper,we use GHRM to measure the catastrophic risk in stop-loss reinsurance. Compared with HRM,the premium is allocated according to the following plan:x to insurer, ln(1+π−x)=π0−x to reinsurer,while π−π0is paid for the fund.On the other hand, some properties of GHRM are demonstrated.Finally,the numerical simulations show the concrete scheme with respect to some distributions,especially for Pareto distribution.

[1]Froot K A.The market for catastrophe risk:A clinical examination.J.Finance Econom., 2001,60(2):529–571.

[2]Froot K A.Risk management,capital budgeting,and capital structure policy for insurers and reinsurers.J.Risk Insurance,2007,74:273–299.

[3]Cummins J D,Doherty N,Lo A.Can insurers pay for the“big one”?Measuring the capacity of insurance market to respond to catastrophic losses.J.Bank Finance,2002,26:557–583.

[4]Klein R W,Wang S.Catastrophe risk fi nancing in the United States and the European Union: A comparative analysis of alternative regulatory approaches.J.Risk Insurance,2009,76(3): 607–637.

[5]Lewis C M,Murdock K C.The role of government contracts in discretionary reinsurance market for natural disasters.J.Risk Insurance,1996,63:567–597.

[6]Cummins J D,Lewis C M,Phillips R D.Pricing Excess of Loss Reinsurance Contracts Against Catastrophic Loss.in:Froot K.The Financing of Catastrophe Risk.Chicago:The Univ.of Chicago Press,1999.

[7]Bernard C,Tian W.Optimal reinsurance arrangements under tail risk measures.J.Risk Insurance,2009,76(3):709–725.

[8]Tan K S,Weng C,Zhang Y.Optimality of general reinsurance contracts under CTE risk measure.Insurance Math.Econom.,2011,49(2):175–187.

[9]Haezendonck J,Goovaerts M J.A new premium calculation principle based on Orlicz norms. Insurance Math.Econom.,1982,1(1):41–53.

[10]Goovaerts M J,Kaas R,Dhaene J,Tang Q.Some new classes of consistent risk measures. Insurance Math.Econom.,2004,34(3):505–516.

[11]Dhaene J,Vandu ff el S,Tang Q,Goovaerts M J,Kaas R,Vyncke D.Capital requirements,risk measures and comonotonicity.Belg.Actuar.Bull.,2004,4(1):53–61.

[12]Goovaerts M J,Kaas R,Laeven R,Tang Q.A comonotonic image of independence for additive risk measures.Insurance Math.Econom.,2004,35(3):581–594.

[13]Denuit M,Dhaene J,Goovaerts M,Kaas R.Actuarial Theory for Dependent Risks:Measures, Orders and Models.Chichester:John Wiley&Sons,Ltd,2005.

[14]Dhaene J,Vandu ff el S,Goovaerts M J,Kaas R,Tang Q,Vyncke D.Risk measures and comonotonicity:A review.Stoch.Models,2006,22:573–606.

[15]Rao M M,Ren Z D.Theory of Orlicz Spaces.New York:Marcel Dekker Inc.,1991.

[16]Bellini F,Rosazza Gianin E.On Haezendonck risk measures.J.Bank Finance,2008,32: 986–994.

[17]Kaas R,Goovaerts M J,Dhaene J,Denuit M.Modern Actuarial Risk Theory.Dordrecht: Kluwer Academic Publishers,2001.

[18]Bellini F,Rosazza Gianin E.Optimal portfolios with Haezendonck risk measures.Statist. Decisions,2008,26:89–108.

62P05,91B30,97M30

A

1674-5647(2012)04-0367-09

1 Introduction

Insurance companies need reinsurance to limit their liabilities on catastrophe risk.Even if reinsurance prices are high relative to expected loss,risk-averse insurers are still willing to seek reinsurance protections against large events(see[1–2]).Actually,as Cummins et al. declared in[3],the enormous loss would stress the capacity of the insurance underwriting and threaten the credit risk of many reinsurance companies.Catastrophe Fund can improve the availability and a ff ordability of the insurance industry by reimbursing the insured a portion of their catastrophic losses.

Most Catastrophe Fund comes from government program(see[4]).Following the assumption in[5–6],we suggest a Catastrophe fund that limits the taxpayer’s exposure to the catastrophic disaster and reduces cross-subsidization of high-risk insurers by low-riskinsurers in the reinsurance market.

date:Sept.25,2011.

The NSF(10971081,11001105,11071126,10926156,11071269,J0730101)of China,Specialized Research Fund(20070183023)for the Doctoral Program of Higher Education,Program(NCET-08-237)for New Century Excellent Talents in University,Scienti fi c Research Fund(200810024,200903278)of Jilin University, and 985 project of Jilin University.