Fourier Moment Method with Regularization for the Cauchy Problem of Helmholtz Equation∗

MA YUN-yUN AND MA FU-MING

(School of Mathematics,Jilin University,Changchun,130012)

Fourier Moment Method with Regularization for the Cauchy Problem of Helmholtz Equation∗

MA YUN-yUN AND MA FU-MING

(School of Mathematics,Jilin University,Changchun,130012)

In this paper,we consider the reconstruction of the wave fi eld in a bounded domain.By choosing a special family of functions,the Cauchy problem can be transformed into a Fourier moment problem.This problem is ill-posed.We propose a regularization method for obtaining an approximate solution to the wave fi eld on the unspeci fi ed boundary.We also give the convergence analysis and error estimate of the numerical algorithm.Finally,we present some numerical examples to show the e ff ectiveness of this method.

Fourier moment method,Cauchy problem,Helmholtz equation,regularization,ill-possedness

In this paper,a numerical method for reconstructing the wave fi eld and its normal derivative on∂ΩΓ is proposed.The main idea is to transform the Cauchy problem into a Fourier moment problem,whose solution has an expansion with respect to trigonometric polynomials.The wave fi eld and its normal derivative on the unspeci fi ed boundary can be obtained by solving the corresponding Fourier moment problem.Then we only need to solve the boundary value problems for the Helmholtz equation,i.e.Dirichlet,Neumann or mixed boundary value problems(see[2,14–17]).

The layout of the paper is as follows.In Section 2,we transform the Cauchy problem into a Fourier moment problem.In Section 3,the numerical method with regularization for solving the Fourier moment problem is proposed.The convergence analysis and error estimate are also presented.Then we give the numerical algorithm for solving the normal derivative of the wave fi eld on∂ΩΓ in this section.We present several numerical examples to illustrate the competitive behavior of the method in Section 4.Some conclusions are given in Section 5.

2 Formulation of the Fourier Moment Problem

Let Ω be a bounded and simply connected domain in R2,whose boundary∂Ω is sufficiently smooth.Γ is an open part of the boundary∂Ω in the half plane{(x,y)|y≥ 0}which connects two points(0,0)and(1,0).is supposed to be a special curve.

For s∈R,we denote the Sobolev space on Γ byConsider the following Cauchy problem:

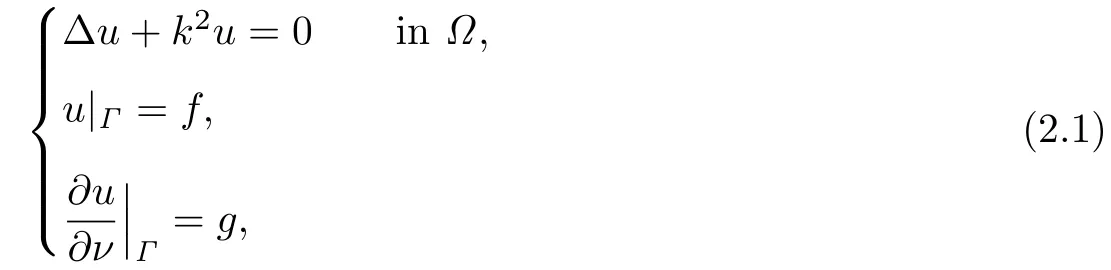
where k＞0 is the wave number and ν is the unit outward normal to the boundary Γ.In this paper,we assume that u(0,0)=u(1,0).

Forn∈Z,let

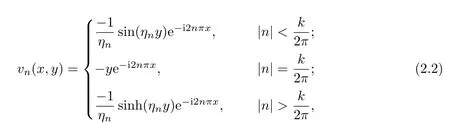
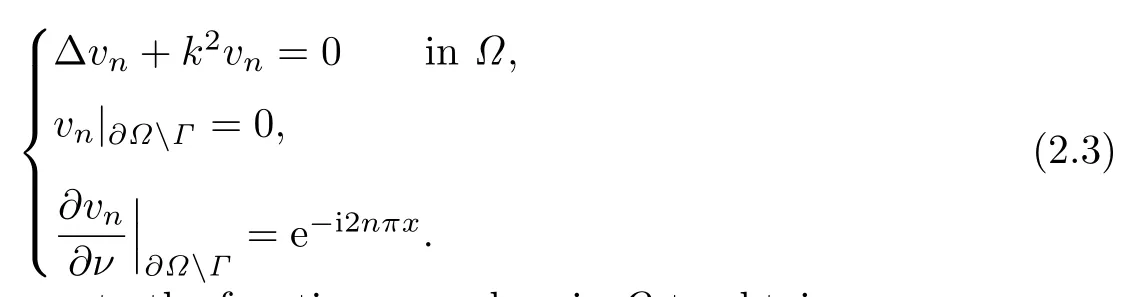
We apply Green’s second t∫heorem to the fun∫cti ons u and vnin Ω to obtain

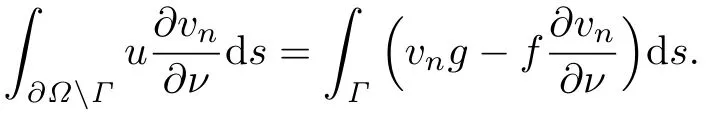
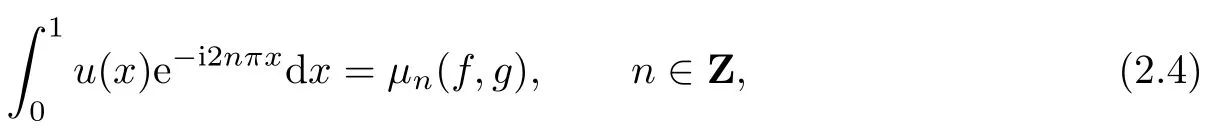
where

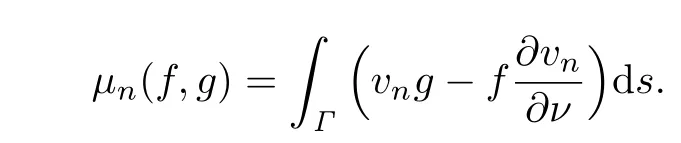
We abbreviateµn=µn(f,g).

For s∈Z,let Hs([0,1])denote the Sobolev space on∂ΩΓ.The inner product and norm in Hs([0,1])are de fi ned by

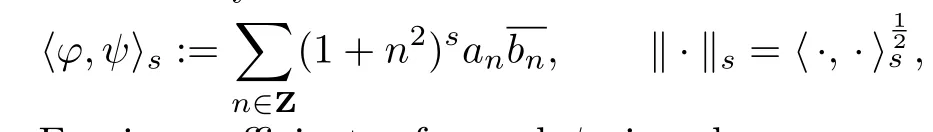
where anand bnare Fourier coefficients of φ and ψ given by

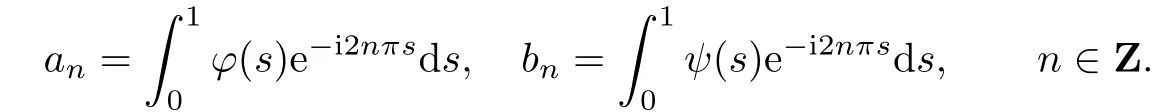
By the above deduction,the Cauchy problem(2.1)can be transformed into the following∈Fourier moment problem: fi nd β(x)([0,1])such that

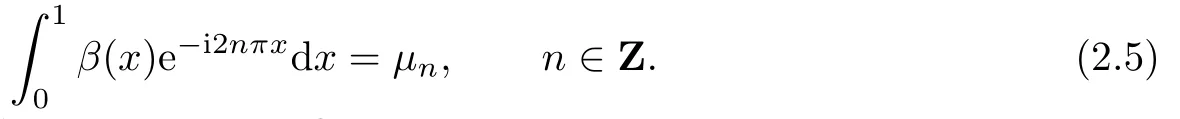
Let Hs(Ω)denote the Sobolev space in Ω,where

Theorem 2.1Suppose that the Cauchy problem(2.1)has a solution u∈H2(Ω).Then

3

Γ. the Fourier moment problem(2.5)has a unique solution β in H2([0,1])and β=u on∂ΩFurthermore,the solution β has an expansion with respect to the trigonometric polynomials of the form

In the following sections,we assume that the Cauchy problem has a solution in H2(Ω). From Theorem 2.1,we see that the solution of(2.5)is unique.But this problem is ill-posed. Small variations in f and g may lead to large di ff erence in β.For example,let

Denote

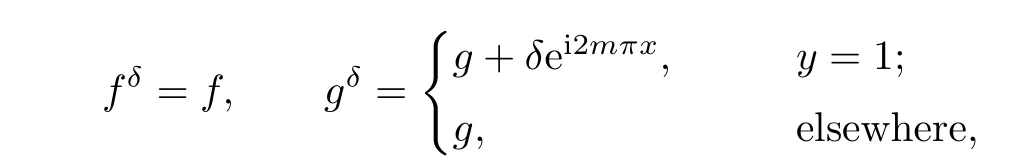
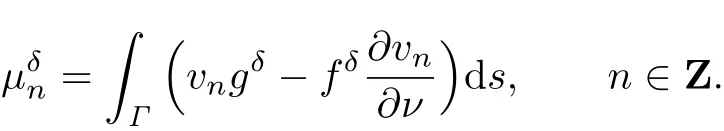
We have

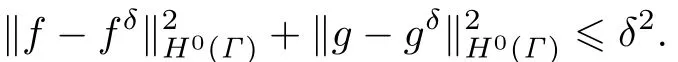
But

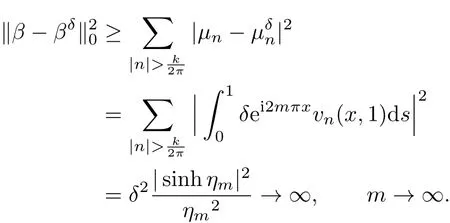
Therefore,for stably solving the Fourier moment problem(2.5),regularization techniques are required.

Remark 2.1Note that∂ΩΓ is supposed to be a special domain[0,1].For a general domain[a,b],we use the following coordinate transformation:

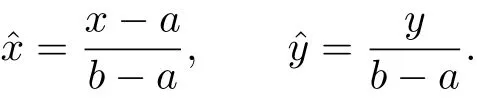
Let

We have

Denote

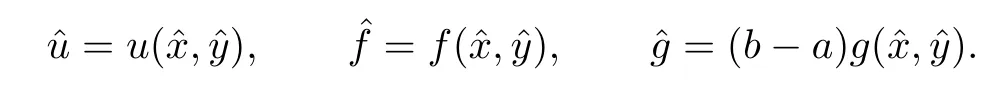
Thusˆu is the solution of the following Cauchy problem of the Helmholtz equation:

Then we use the Fourier moment method to solve(2.7).

Remark 2.2If u(0,0)=a and u(1,0)=b do not satisfy a=b.Denote

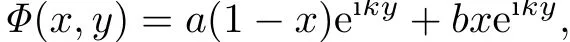
and W=u−Φ.We have W(0,0)=W(1,0)=0 and

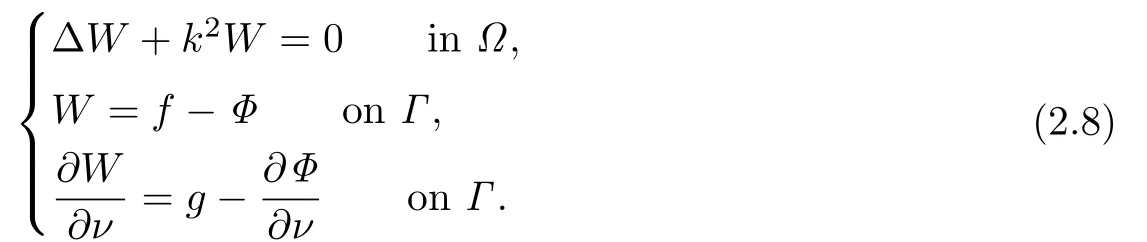
Then we use the Fourier moment method to solve(2.8).The solution of(2.1)is W+Φ.

3 Regularization Method

Recalling the example in Section 2,we see that the instability of the Fourier moment problem (2.5)comes from the highly oscillatory modes.Therefore we construct the regularization by damping the factors sinh(ηny).be a constant depending on Ω.For n∈Z,we use

to replace vn,where Rn(α)is de fi ned by

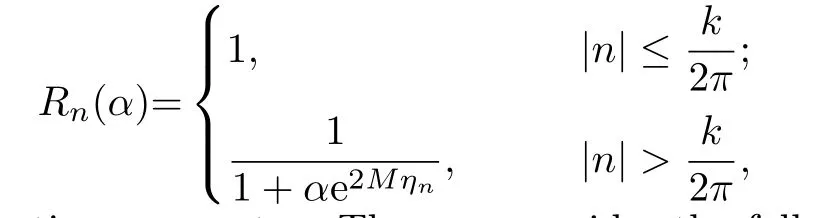
and α＞0 is a regularization parameter.Then we consider the following modi fi ed Fourier moment problem:

Given f,g∈H0(Γ), fi nd a function([0,1])to satisfy

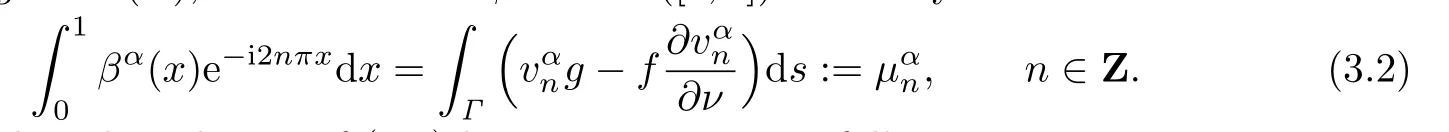
It is obvious that the solution of(3.2)has an expansion as follows:

Theorem 3.1Let f,g∈H0(Γ).Suppose that the Cauchy problem(2.1)has a solution in H2(Ω).Then we have

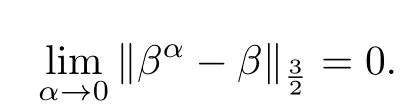
Proof. From Theorem 2.1 and the de fi nition of Sobolev space Hs([0,1]),given ε＞ 0, there exists an N ∈N such that

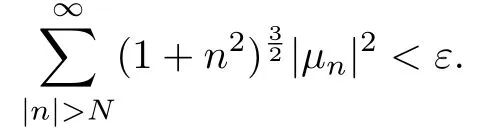
Without loss of generality,we assume that N ＞From(2.2)and(3.1)we can obtain

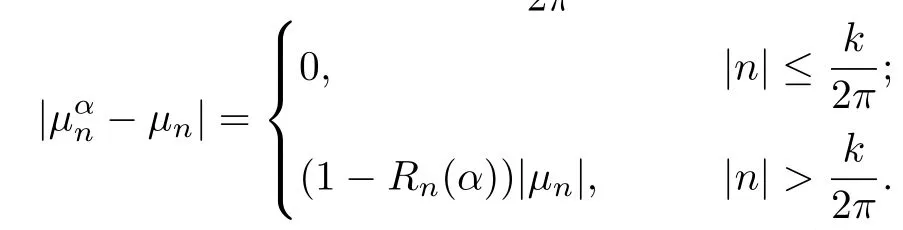
By simple calculation,we get the following properties of 1−Rn(α):

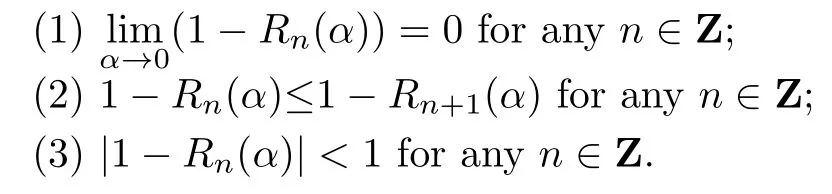
Then we have

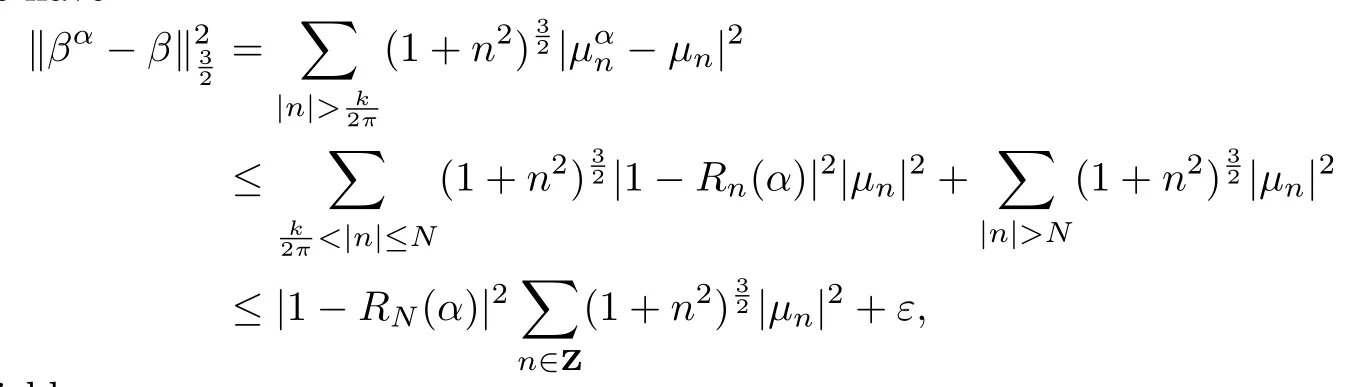
which yields

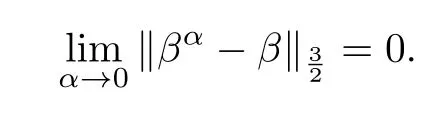
This completes the proof.

In practice,the Cauchy data is never known exactly,but only up to an error of δ＞ 0. Assume that we know δ＞0 and fδ,gδ∈H0(Γ)with

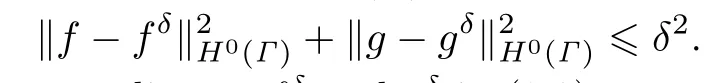
The Fourier moments correspond∫ing( to fδand gδi)n(3.2)are

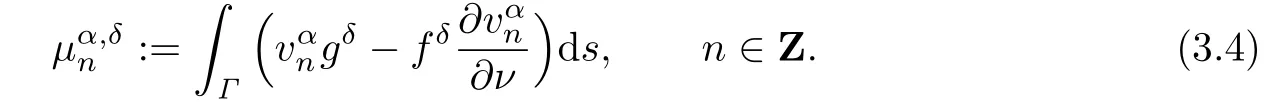
Subtracting(3.2)from(3.4)yields that

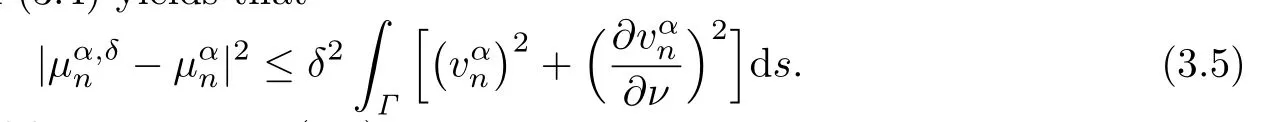
By the de fi nition of functionin(3.1),we have

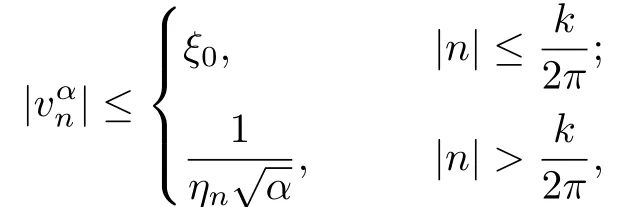
is a constant depending on Ω and k.Similarly,we can obtain that

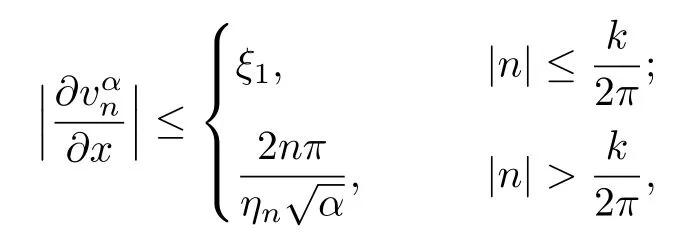
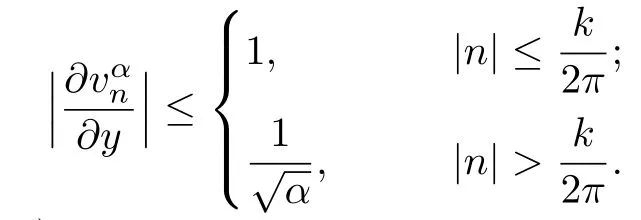
Then the error bound of(3.5)is

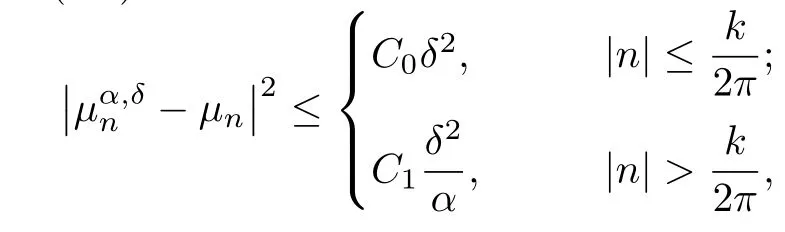
where

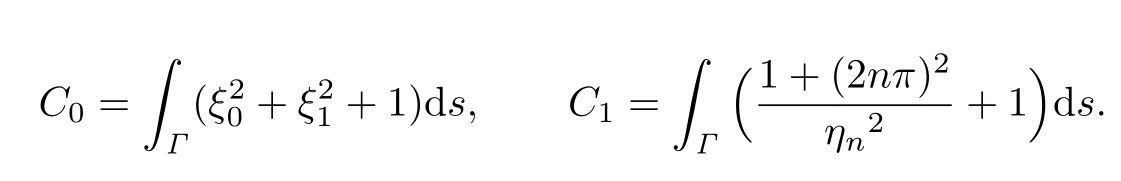
They are independent of n.

Instead of using the in fi nite summation in the equation(3.3),the solution of(2.5)is approximated by a fi nite summation,i.e.,

Let TNdenote the 2N+1-dimensional trigonometric polynomial space

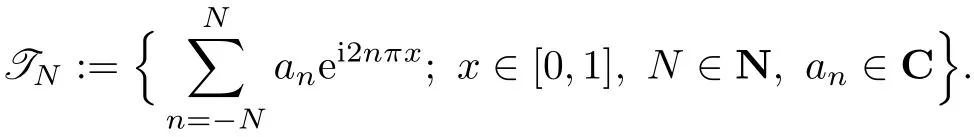
For s≥0,the projection operator PN:Hs([0,1])→TNis given by

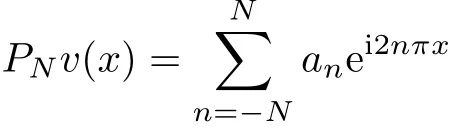
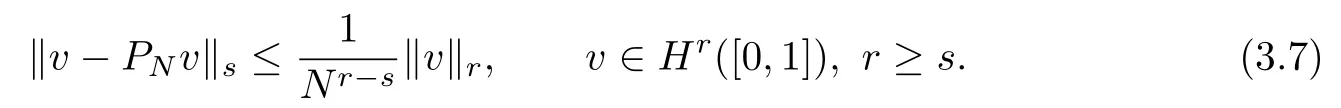
A complete discussion including proofs on the properties of PNcan be found in[18].

After these preparations,we can obtain the following error estimate.

Theorem 3.2Suppose that u is a solution of the problem(2.1)satisfying

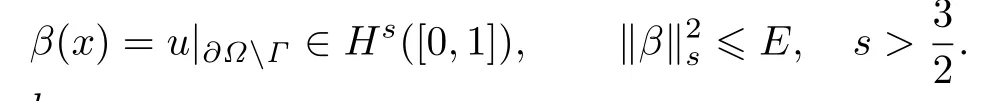
Given N∈N,we choose

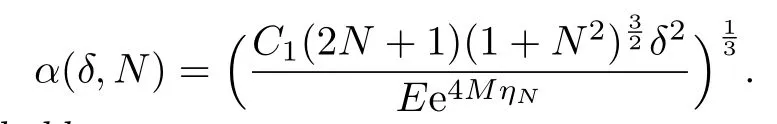
The following estimate holds:

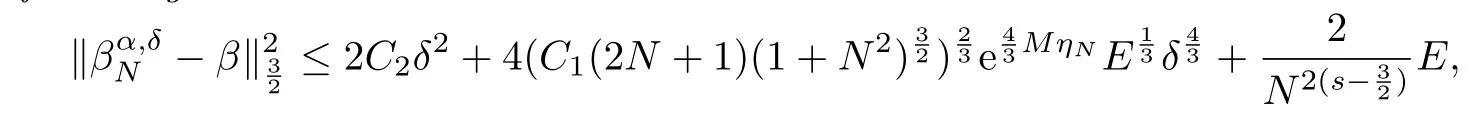
where

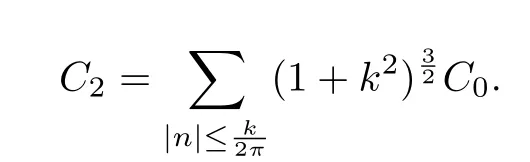
Furthermore,if we take

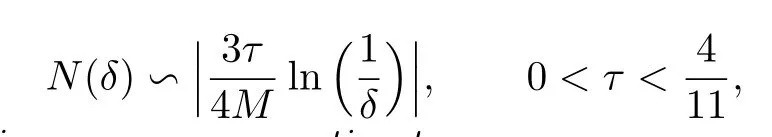
then we have the following convergence estimate:

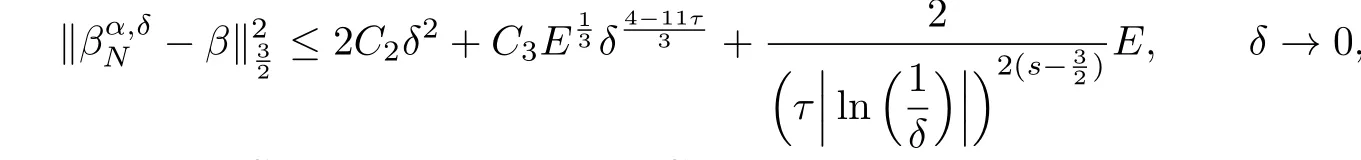
where the constant C3depends on M and C1.

Proof. From the triangle inequality,we know that

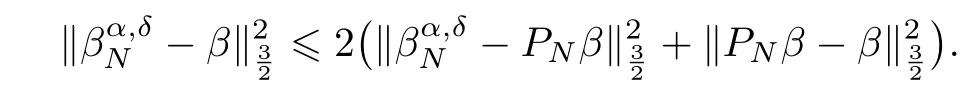
From the above deduction,we have

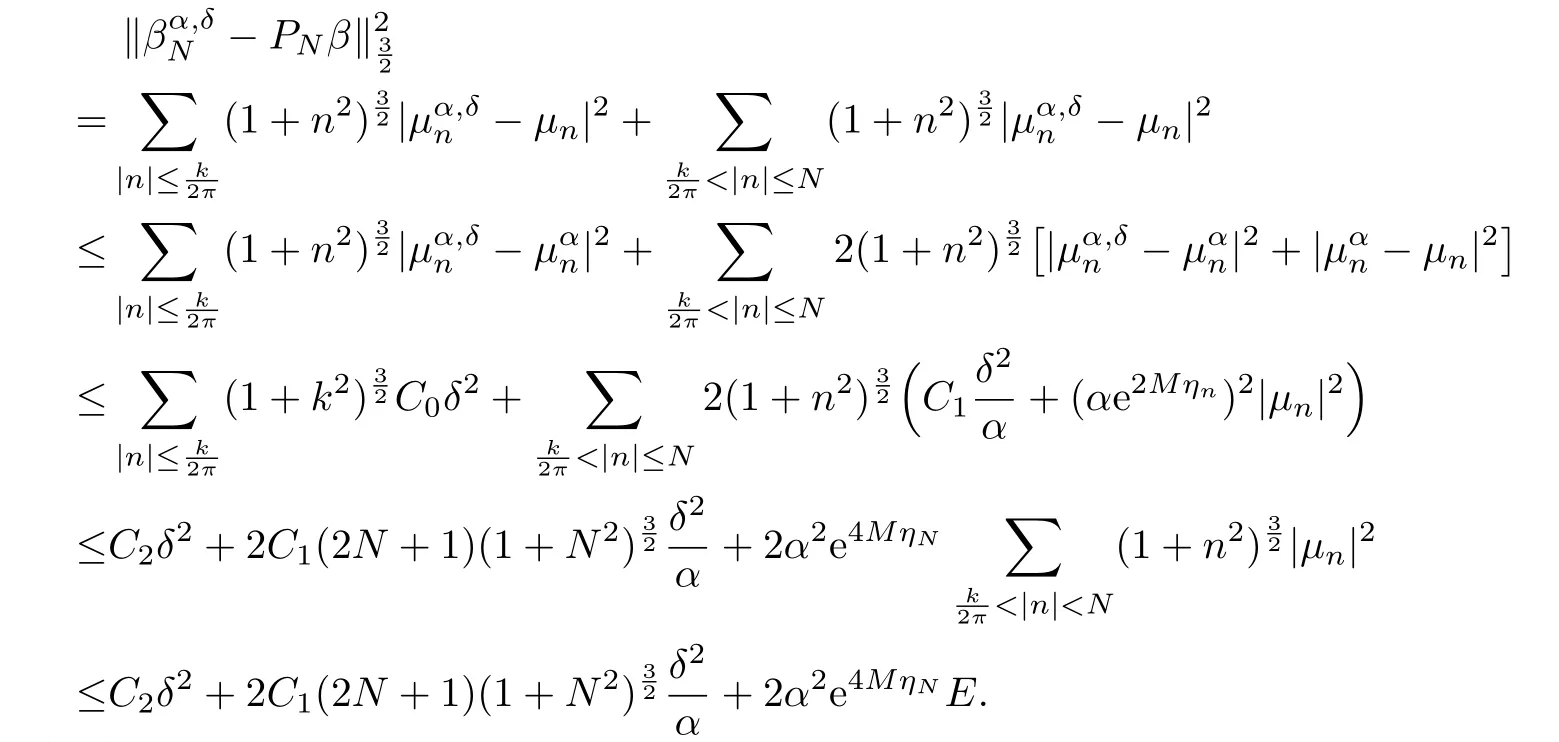
By(3.7),the choice of

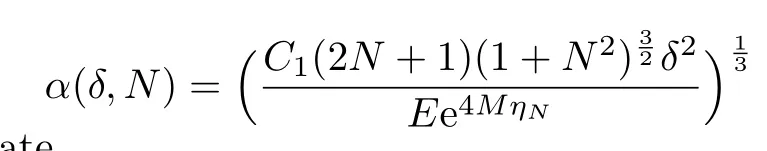
leads to the error estimate.

At last,we give the Fourier moment method for solving the normal derivative of the wave fi eld u on∂ΩΓ.We assume that

For n∈Z,le

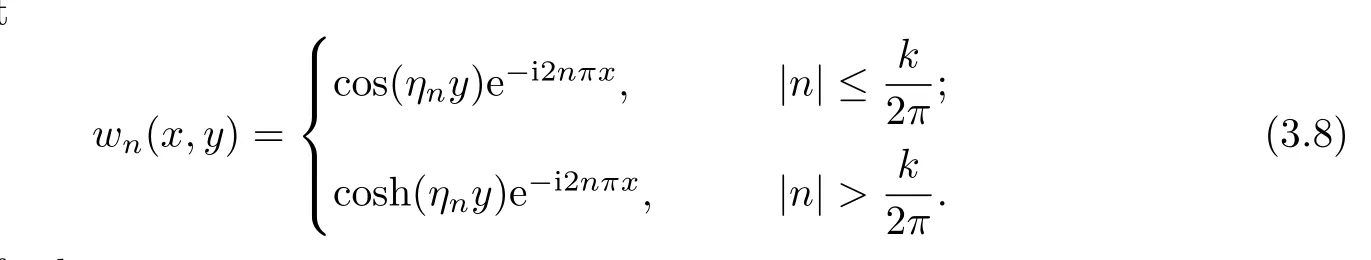
It is easy to verify that

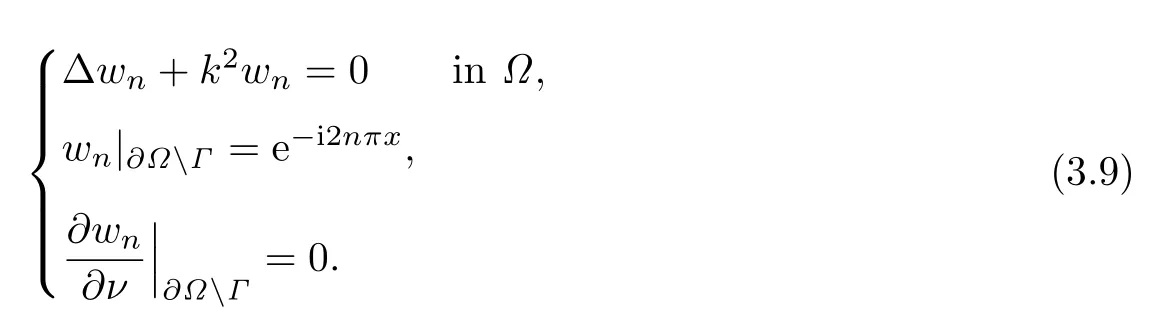
Applying Green’s second theorem to the function u and vnin Ω,we obtain

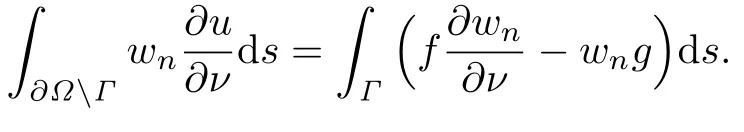
Denote We have

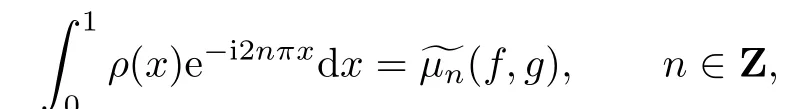
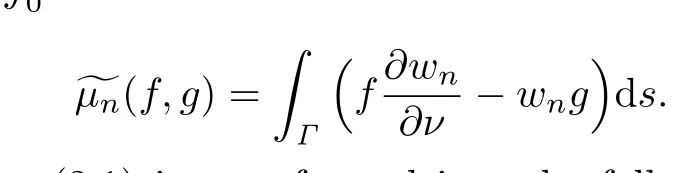
where

Then the Cauchy problem(2.1)is transformed into the following moment problem: fi nd∈ρ([0,1])such that

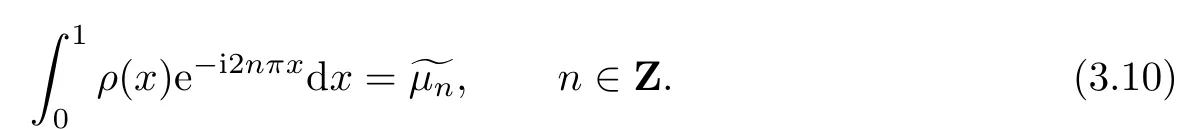
The solution ρ of(3.10)has an expansion of the form

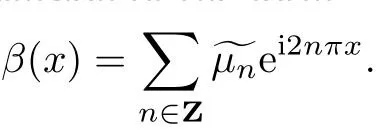
We give the following regularization method for damping cosh(ηny).

For n∈Z,wnis replaced by=Tn(α)wn,where Tn(α)is de fi ned by

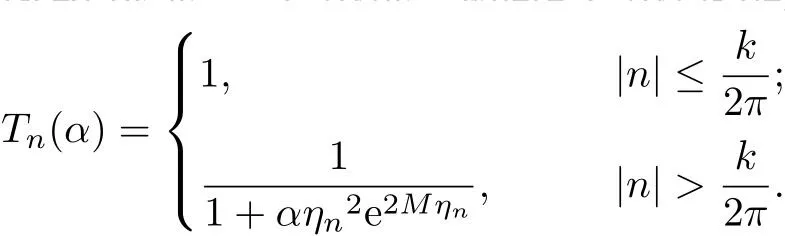
We solve the following modi fi ed Fourier moment problem.Given f,g∈ H0(Γ), fi nd a

α∈function ρ([0,1])satisfying

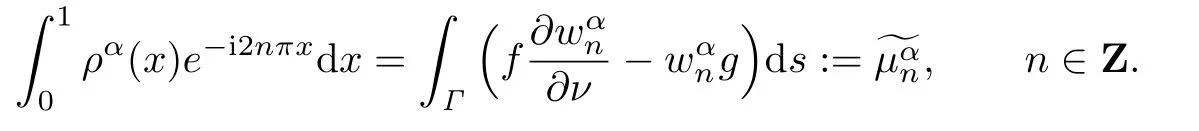
Then we use

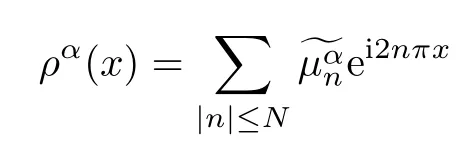
to approximate the solution of(3.10).

The convergence analysis of this method is the same as the Fourier moment method for solving the wave fi eld u on∂ΩΓ.We omit it here.

4 Numerical Results

In this section,some numerical tests are presented in order to show the Fourier moment method with regularization works.These numerical experiments are accomplished by Matlab.Given L＞0,let

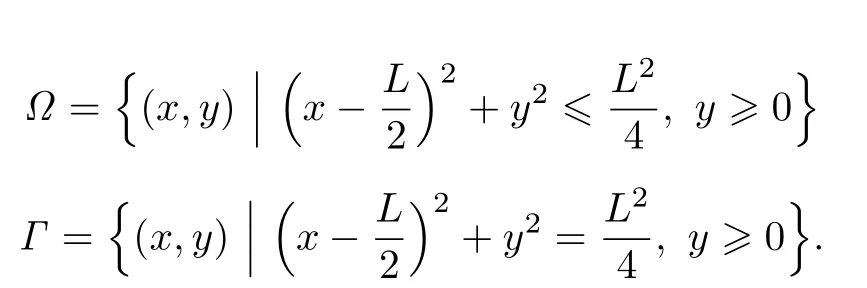
and

The relative noise level is δ.Denote by fδ,gδthe noise data for the wave fi eld and its normal derivative respectively.We have

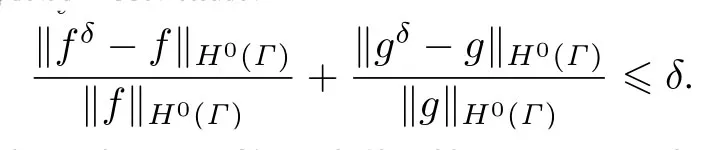
Denote by β the exact value of u on Γ and βNthe numerical approximate solution of β, where u is the exact solution of(2.1).

Example 4.1Let L=1.We choose

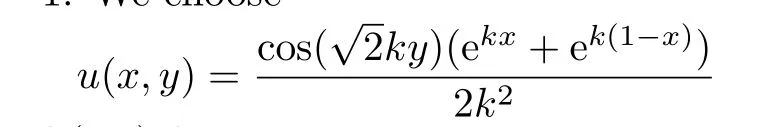
to be the exact solution of(2.1)for the wave number k=5.The numerical results for the approximate solution βNfor N=3,10 and the exact solution β are presented in Fig.4.1. It shows that the numerical algorithm is convergent.But the numerical solution βNfor N=12 has large errors as α=0.It is useless.Then we choose α=5e−51.The results of them are given in Fig.4.2.We can conclude that our regularization method is e ff ective.

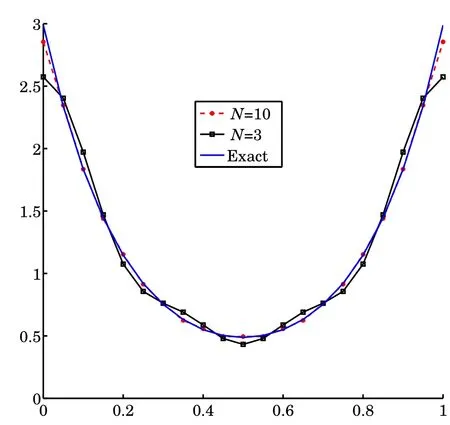
Fig.4.1

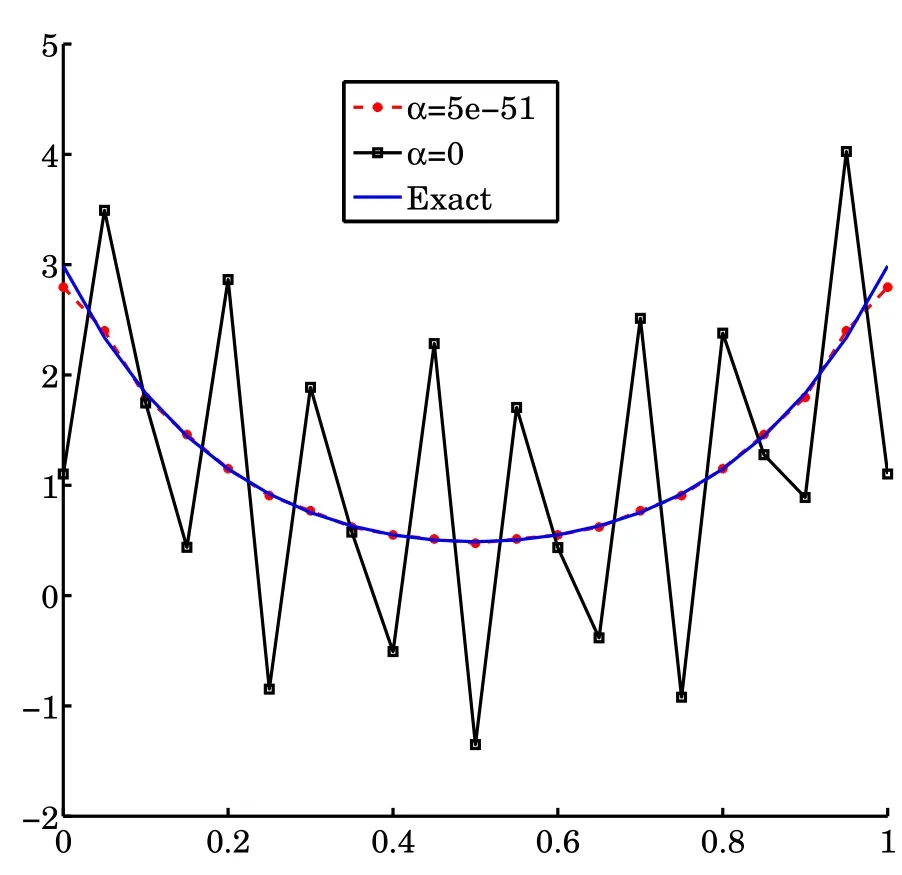
Fig.4.2

Next we consider the inverse di ff raction problem.

Let I be a bounded connected aperture on y=0.We attempt to reconstruct the shape of I from the knowledge of the di ff racted wave fi eld and its normal derivative on a half circle Γ.Our problem is formulated as follows.

Given functions f and g, fi nd a function β satisfying

where u satis fi es

with the Sommerfeld radiation condition

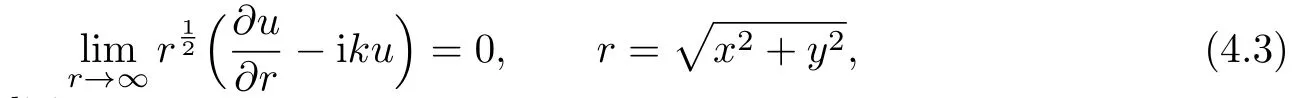
and the Cauchy condition

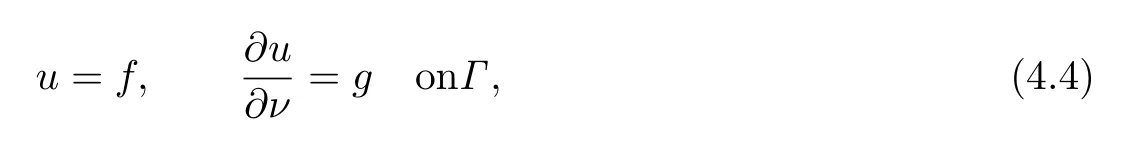
We suppose that I=suppβ⊂∂ΩΓ.The Cauchy data is created by solving the problem (4.1)–(4.3)for a giving β.Then we use the Fourier moment method to solve β satisfying (4.1),where the wave fi eld u satis fi es(4.2)in Ω and Cauchy boundary condition(4.4)on Γ.We reconstruct the shape of I as follows.

Given a constant c＞0,let

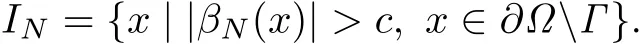
Then I is approximated by IN.In the following example,we choose k=20,N=50,

Example 4.2In the fi rst case,f,g are created by β(x)=1 on I.The results of β and βNare shown in Fig.4.3.In the second case,f,g are created by β(x)=(x−π)(x−3π) on I.The results of β and βNare shown in Fig.4.4.Then we add the random noise in the second case.The relative noise level is 0.02.the results of β and βNare shown in Fig. 4.5.Choosing c=0.8,we get suppβN≈[π,3π]in both cases.They demonstrate that our method is stable and accurate.>

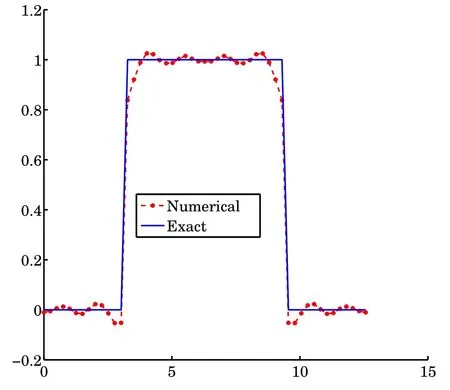
Fig.4.3

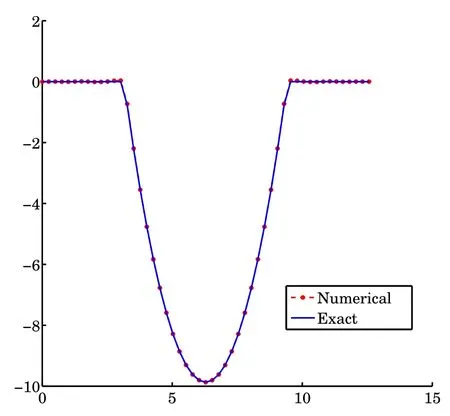
Fig.4.4

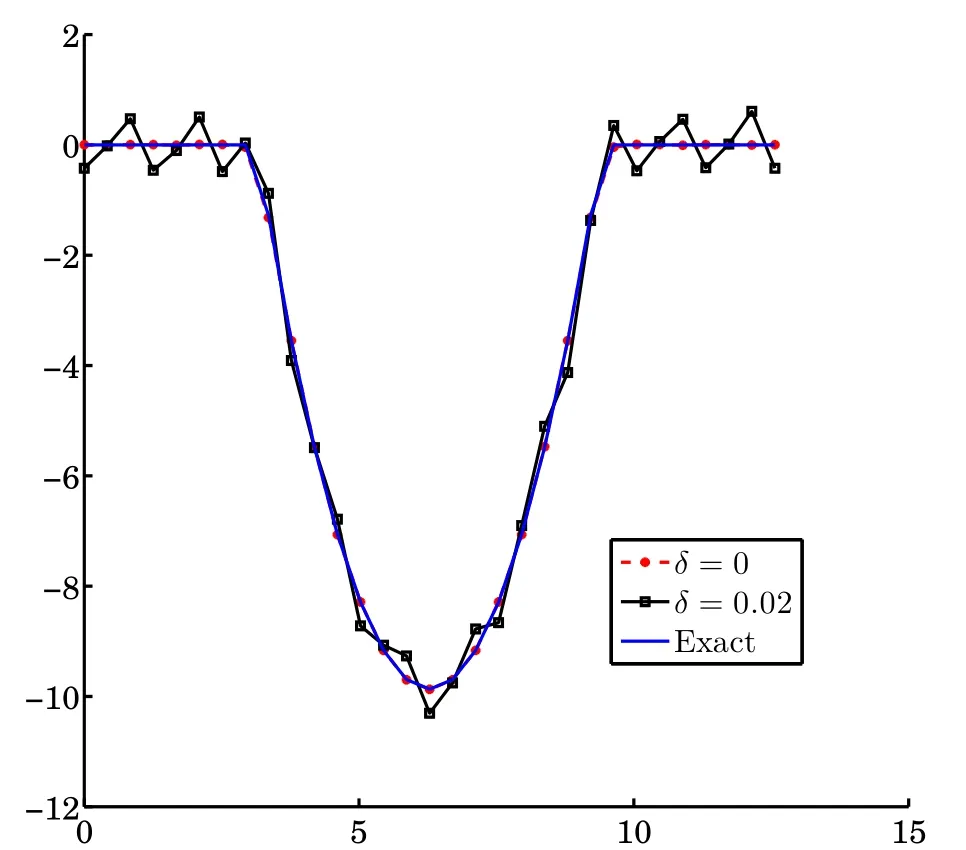
Fig.4.5

5 Conclusion

In this paper,we propose a Fourier moment method with regularization for solving the Cauchy problem of the Helmholtz equation in a bounded domain.The convergence analysis and error estimate have also been given.The numerical examples show that our method is accurate,stable and e ff ective.

[1]Ammari H,Bao G,Wood A W.An integral equation method for the electromagnetic scattering from cavities.Math.Methods.Appl.Sci.,2000,23:1057–1072.

[2]Beskos D E.Boundary element method in dynamic analysis:Part II(1986-1996).ASME Appl. Mech.Rev.,1997,50:149–197.

[3]Kern D Q,Kraus A D.Extended Surface Heat Transfer.New York:McGraw-Hill,1972.

[4]Harari I,Barbone P E,Slavutin M,Shalom R.Boundary in fi nite elements for Helmholtz equation on exterior domains.Internat.J.Numer.Methods Engrg.,1997,41:1105–1131.

[5]Colton D,Kress R.Inverse Acoustic and Electromagnetic Scattering Theory.New York: Springer,1992.

[6]Isakov V.Inverse Problems for Partial Di ff erential Equations.New York:Springer,1998.

[7]Yu C,Zhou Z F,Zhuang M.An acoustic intensity-based method for reconstruction of radiated fi elds.J.Acoust.Soc.Amer.,2008,123:1892–1901.

[8]Yu C,Zhou Z F,Zhuang M,Li X D,Thiele F.3-D Acoustic Intensity-based Method and Its CAA Applications.14th AIAA/CEAS Aeroacoustic Conference(29th Aeroacoustic Conference),May,5-7,Vancoucer-British-Columbia-Canada,2008.

[9]Eld´en L,Berntsson F,Regin´ska T.Wavelets and Fourier methods for solving the sideways heat equation.SIAM J.Sci.Comput.,2000,21:2187–2205.

[10]Marin L,Elliott L,Hegges P J,Ingham D B,Lesnic D,Wen X.An alternating iterative algorithm for Cauchy problem associated to the Helmholtz equation.Comput.Methods Appl. Mech.Engrg.,2003,192:709–722.

[11]Marin L,Elliott L,Hegges P J,Ingham D B,Lesnic D,Wen X.Conjugate gradient boundary element solution to the Cauchy problem for Helmholtz-type equations.Comput.Mech.,2003, 31:367–377.

[12]Marin L,Lesnic D.The method of fundamental solutions for Cauchy problem associated with two-dimensional Helmholtz-type equations.Comput.&Structures,2005,83:267–278.

[13]Wei T,Qin H H,Shi R.Numerical solution of an inverse 2D Cauchy problem connected with the Helmholtz equation.Inverse Problems,2008,24:1–18.

[14]Chen J T.Recent development of dual BEM in acoustic problems.Comput.Methods Appl. Mech.Engrg.,2000,188:833–845.

[15]Harari I.A survey of fi nite element methods for time-harmonic acoustics.Comput.Methods Appl.Mech.Engrg.,2006,195:1594–1607.

[16]Isakov V,Wu S F.On theory and application of Helmholtz equation least squares method in inverse acoustic problems.Inverse Problems,2002,18:1147–1159.

[17]Colton D,Kress R.Integral Equation Methods in Scattering Theory.New York:Wiley-Interscience Publication,1983.

[18]Krish A.An Introduction to the Mathematical Theory of Inverse Problem.NewYork:Springer-Verlag,1996.

35R30,35R25

A

1674-5647(2012)04-0300-13

1 Introduction

Consider the reconstruction of the wave fi eld in a bounded domain Ω from unexact Cauchy data given on an open part Γ of the boundary∂Ω.This problem is described by a Cauchy problem for the Helmholtz equation,which arises in many physical applications related to wave propagation and vibration phenomena.For example,the acoustic cavity problem,the vibration of a structure,the heat conduction in fi ns,the radiation and scattering of wave (see[1–5]and the references therein).

It is well known that the Cauchy problem for elliptic equations is ill-posed(see[6]). Although the solution of Cauchy problem for the Helmholtz equation is unique,it does not depend continuously on Cauchy data.It implies serious numerical difficulties in solving this problem.However,this case is important from point of view of practical applications for acoustic and electromagnetic fi elds where the exact Cauchy data is approximated by their measurements.Therefore,these are important studies in the literature of the Cauchyproblem for the Helmholtz equation.A number of numerical methods have been proposed to solve this problem.For example,there are the acoustic intensity-based method(see[7–8]),the Fourier regularization method(see[9]),the alternating iterative boundary element method(see[10]),the conjugate gradient boundary element method(see[11]),the method of fundamental solution(see[12]),and the moment method(see[13]).

date:Sept.14,2010.

The NSF(10971083)of China.