基于贝叶斯最优核判别分析的机械故障诊断

郝腾飞，陈 果

(南京航空航天大学 民航学院，南京 210016)

核方法是模式识别领域的一场革命，其基本思想是首先将原始样本通过核函数隐含地映射到一个高维特征空间中，然后在该空间中执行相应的线性算法。由于核函数隐含地实现了一个非线性映射，同时又避开了维数灾难，因此，核方法可高效地解决非线性模式识别问题［1］。机械故障诊断本质上是一个模式识别问题。目前，许多核方法已广泛应用于机械故障诊断。文献［2］与文献［3］分别对支持向量机(support vector machine，SVM)在机械故障诊断中的应用进行了很好的综述。文献［4］研究了核主成分分析(kernel principal component analysis，KPCA)在齿轮故障诊断中的应用。文献［5］将粗糙集理论的属性约简与KPCA结合，提出了一种基于粗糙KPCA的机械故障特征提取方法并将其应用于滚动轴承故障特征提取。文献［6］提出了一种利用KPCA对故障信号的小波尺度谱图像进行特征提取的方法，并将其应用于转子故障诊断。文献［7］研究了核判别分析(kernel discriminant analysis，KDA)在风机与齿轮故障诊断中的应用。

以上研究充分展示了核方法在机械故障诊断中的明显优势。但应用上述各种核方法到机械故障诊断时均存在一个共同的问题，即核参数的选择问题。核参数对各种核方法的性能有很大影响，若核参数选择恰当，则核方法可获得比相应的线性方法更好的性能，否则，甚至可能不及对应的线性方法，因此，在应用核方法时，核参数的选择至关重要。目前，核参数一般通过交叉验证的方法选取，但该方法计算量较大且只能在给定的一组参数中选择一个最优参数，因此不一定能找到全局最优的参数。

许多研究［8－10］表明KDA与SVM具有类似的分类性能，但与SVM相比，KDA在机械故障诊断中的应用研究相对较少。本文研究了KDA在机械故障诊断中的应用。针对KDA中核参数的选择问题，本文采用You等［11］提出的同方差性准则来选择核参数，由于使用该准则可以得到最优的核参数，因此将使用该准则来优化核参数的KDA称为贝叶斯最优KDA。最后建立了一种基于贝叶斯最优KDA的故障诊断模型，并以滚动轴承故障诊断为例研究了该方法在机械故障诊断中的应用。

1 贝叶斯最优核判别分析

1.1 核判别分析

线性判别分析(linear discriminant analysis，LDA)是一种经典的监督特征提取及分类方法，其基本思想是寻找一组投影方向，将原始样本向该组方向上投影后可使不同类别的样本尽量远离，同类样本尽量靠近。如果不同类别样本的分布满足同方差性(即具有相同的协方差矩阵)，则用LDA可求得一个最佳子空间，不同类别的样本向该子空间投影后具有最佳判别性。但实际中不同类别的样本一般很难满足同方差性，为解决该问题，Baudat等［10］与 Mika等［12］分别独立地将核技巧引入LDA，提出了KDA。KDA的基本思想是先用核技巧将原始样本隐含地映射到一个高维特征空间;然后在该特征空间中执行LDA。根据核方法的原理，核技巧隐含地实现了一个非线性映射，从而利用核技巧可使不同类别的样本在高维特征空间中满足同方差性，因此KDA可有效地解决LDA中要求不同类别样本分布满足同方差性的问题。以下具体介绍KDA算法的基本原理。

设有x1，x2，…，xm∈Rnm 个样本，分别属于 c个类别，φ为由核技巧诱导的非线性映射，则KDA的目标函数为:

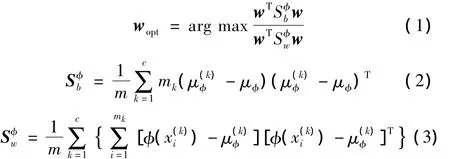
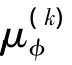
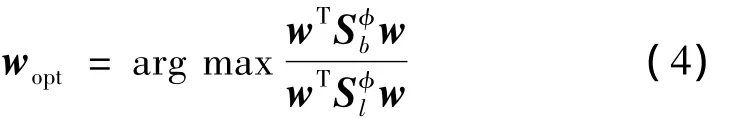
最优投影向量w可通过求解下列广义特征值问题获得:

1.2 贝叶斯最优核判别分析

KDA虽在理论上解决了LDA中类分布的同方差性的假定问题，但实际应用KDA时，由于不同的核参数对应不同的非线性映射，只有选择一个恰当的核参数，才能使不同类别的样本在高维特征空间中满足同方差性，因此应用KDA的关键是选择一个恰当的核参数。目前，核参数一般通过交叉验证的方法进行选取，但该方法计算量较大且只能在给定的一组参数中选择一个最优参数，因此不一定能找到全局最优参数。针对KDA中的核参数选择问题，You等［11］提出了一个同方差性准则Q1:

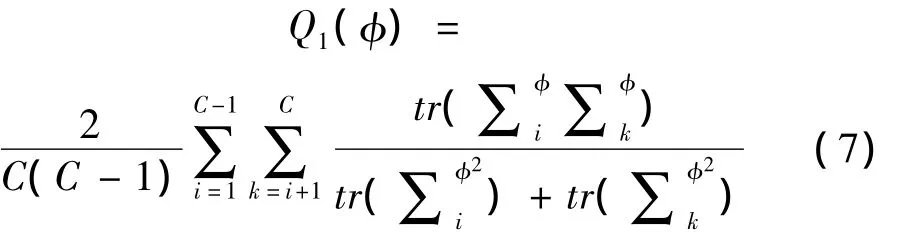
用上述同方差性准则虽可保证各类样本在特征空间中满足同方差性，但将KDA应用于分类问题时，不仅需要各类样本满足同方差性，而且需要各类样本尽量远离，为此You等又引入另一个准则Q2测量各类样本的可分性:

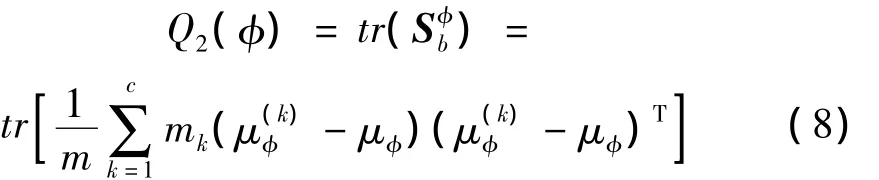
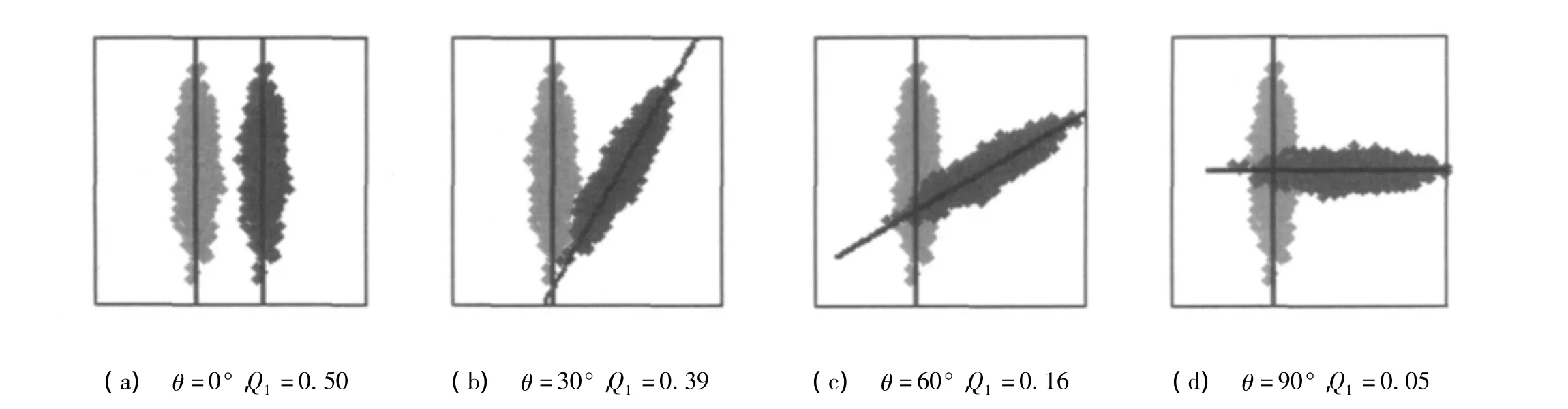
图1 应用同方差性准则的四个例子Fig.1 Four examples of the use of the homoscedastic criterion

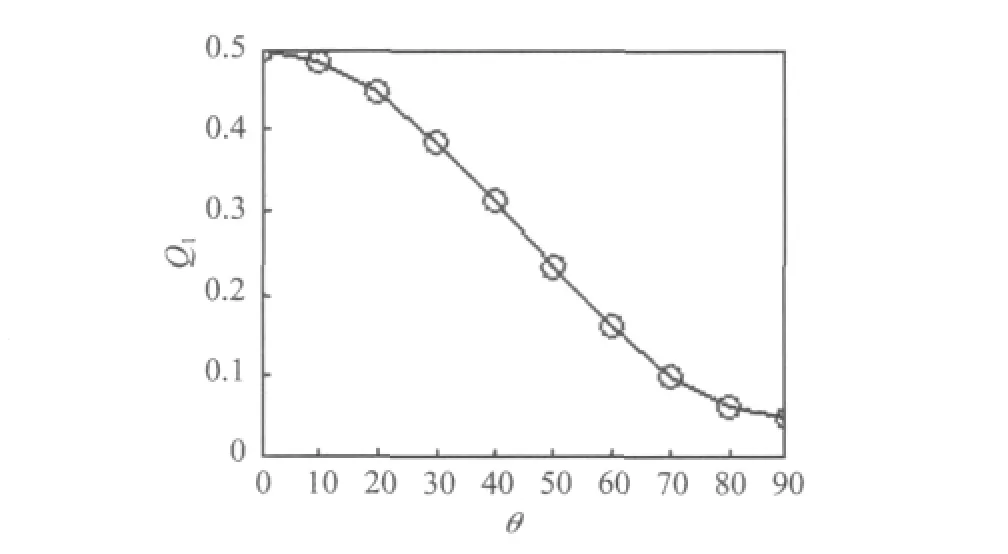
图2 同方差性准则值随两个分布相似性变化关系Fig.2 The relationship between the value of homoscedastic criterion and the similar of two distributions

该准则实际上是特征空间中类间散度矩阵的迹，显然可以用来测量各类样本的可分性。根据以上分析，在应用KDA时，最优核参数应为Q1与Q2同时取最大值时对应的核参数，因此最终准则应为上述两个准则的乘积［11］，即:

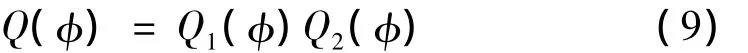
由于测量各类样本可分性的准则比较明显，因此将最终准则仍称为同方差性准则。

在应用KDA时，可用梯度下降法优化上述准则找到最优核参数，该核参数对应的非线性映射可将原始样本映射到一个高维特征空间中，在该空间中不同类别的样本具有相同的协方差矩阵并且相互之间尽量远离。在该空间中应用LDA可求得一个最优的子空间，各类样本向该子空间投影后可获得最佳的判别性。因此，将用上述准则寻找核参数的KDA称为贝叶斯最优KDA。

2 基于贝叶斯最优核判别分析的机械故障诊断方法

基于贝叶斯最优核判别分析的机械故障诊断流程如图3所示。

具体诊断方法如下:

(1)用相关传感器采集反映机械设备运行状态的振动信号;

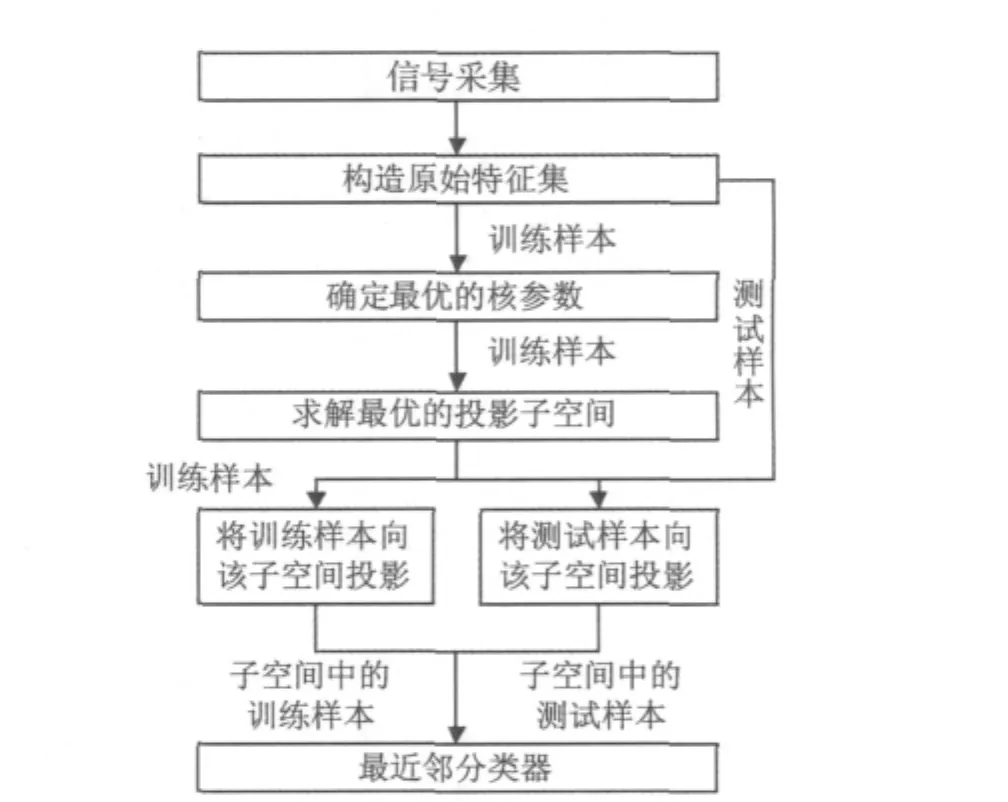
图3 基于贝叶斯最优核判别分析的机械故障诊断流程Fig.3 Flow chart of machinery fault diagnosis based on Bayes optimal kernel discriminant analysis

(2)用各种信号分析技术(如时域分析技术、频域分析技术以及时频域分析技术等)构造原始特征集;

(3)根据(1)和(2)产生一批训练样本的原始特征集，基于该组样本，用梯度下降法优化同方差性准则，确定最优核参数;

(4)基于训练样本的原始特征集，采用最优核参数，用KDA求解一组最优投影向量，该组投影向量张成一个最优子空间;

(5)对于测试样本，首先用与训练样本相同的信号分析技术进行处理，形成测试样本的原始特征集，然后将训练样本与测试样本的原始特征集分别投影到上述最优子空间;

(6)在最优子空间内用最近邻分类器进行故障分类。

3 滚动轴承故障诊断实例

滚动轴承在旋转机械中应用极为广泛，其运行状态往往直接影响到整台机器的精度、可靠性及寿命。由于滚动轴承的寿命离散性很大，无法进行定时维修，因此，对滚动轴承实施状态监测与故障诊断具有重要意义［13］。本文以滚动轴承故障诊断为例，研究了贝叶斯最优核判别分析在机械故障诊断中的应用。实验数据采用美国Case Western Reserve University电气工程实验室的滚动轴承实验台数据［14］。在该实验台中，实验轴承支撑电机转轴，在其内圈、外圈及滚动体上分别用电火花技术加工单点损伤，以模拟内圈故障、外圈故障与滚动体故障。在轴承座上方设置加速度传感器测试轴承振动信号，采样频率为12 kHz。选取正常样本、内圈故障样本、外圈故障样本及滚动体故障样本各200个。每个样本的数据点为4 096个。将每一种状态的样本随机选取一半用于训练，一半用于测试，即训练样本和测试样本均为400个。

用两种方法构造原始特征集。第一种首先计算原始振动信号的均值、有效值、峰值、波形指数、波峰指数、冲击指数、裕度指数、歪度指数及峭度指数，然后由这9个时域特征组成原始特征集。第二种用经验模式分解［15］构造原始特征集，具体方法为首先使用经验模式分解，将原始振动信号分解为一系列本征模函数分量之和，由于滚动轴承的故障信息主要包含在高频段且分解得到的本征模函数分量依频率从高到低排列，据大量实验分析、比较，发现前4个本征模函数分量一般包含了滚动轴承故障的特征信息，因此选取前4个本征模函数分量并求其相应的包络谱，然后从各包络谱中提取旋转频率、内圈故障特征频率、外圈故障特征频率及滚动体故障特征频率的包络谱值，其中每个包络谱值均取4个本征模函数分量包络谱中的最大值，最后用本征模函数分量的这4个包络谱值形成原始特征集。

用KDA可获得的子空间维数最高为C－1，其中C为样本的类别数。在本文实验中，滚动轴承样本包括正常、内圈故障、外圈故障及滚动体故障4种类型，因此子空间的维数最高为3。为检验本文方法的性能，同时使用KPCA，LDA与SVM进行故障诊断。其中基于KPCA和LDA的故障诊断方法与KDA类似，即首先使用这两种方法将原始特征集投影到一个三维子空间中，然后在相应的子空间内使用最近邻方法进行故障分类。实验中，所有核方法的核函数均选用高斯核函数，KDA的核参数通过优化同方差性准则获得，KPCA的核参数，SVM的核参数及正则化参数均用十折交叉验证方法选取。

根据上述实验方法，对于KPCA，LDA与KDA首先用训练样本的原始特征集求解各自的最优子空间，然后将训练样本和测试样本的原始特征集分别投影到相应的子空间，其中测试样本的投影结果如图4、图5所示。图4为时域特征的投影结果，图5为包络谱特征的投影结果。从两图中可以看出，对时域特征和包络谱特征，KPCA和LDA的投影结果中均有一部分样本发生了重叠，而在KDA的投影结果中四种状态样本相互分离，可分性均非常好。对上述三种方法进一步基于投影后的样本用最近邻方法进行故障分类，对SVM则直接基于原始特征集进行故障分类，分类结果如表1、表2所示。表1为时域特征的诊断结果，表2为包络谱特征的诊断结果。由两表可以看出，对时域特征和包络谱特征，KDA的诊断结果均优于KPCA和LDA的诊断结果，与SVM的诊断结果相当，且对各种状态样本的分类正确率均达到了100%。实验中，KDA作为一种监督学习方法，在训练中利用了类标号信息，因此故障诊断的性能明显优于无监督的学习方法KPCA;同时由于KDA使用了核技巧，因此其故障诊断的性能同样优于线性方法LDA;与SVM相比，KDA获得了同样的故障诊断性能，但是通过引入同方差性准则，KDA实现了核参数的自动选取。

为进一步说明同方差性准则在优化KDA核参数中的有效性，图6、图7给出了KDA用于时域特征时的参数优化过程。图6为同方差性准则值随迭代次数的变化过程:随着迭代次数的增加，同方差性准则的值逐渐增大，最终稳定于一个最大值;图7为分类识别率随迭代次数的变化过程:随着迭代次数的增加，分类识别率逐渐增加，最终达到100%。综合图6、图7可以看出，分类识别率随同方差性准则值的增大而增加，在同方差性准则值取最大时，分类识别率达到最高，表明同方差性准则可有效地用于KDA中的核参数优化。

图4 时域特征的投影结果Fig.4 Projective results of the time domain features

图5 包络谱特征的投影结果Fig.5 Projective results of the envelope spectrum features

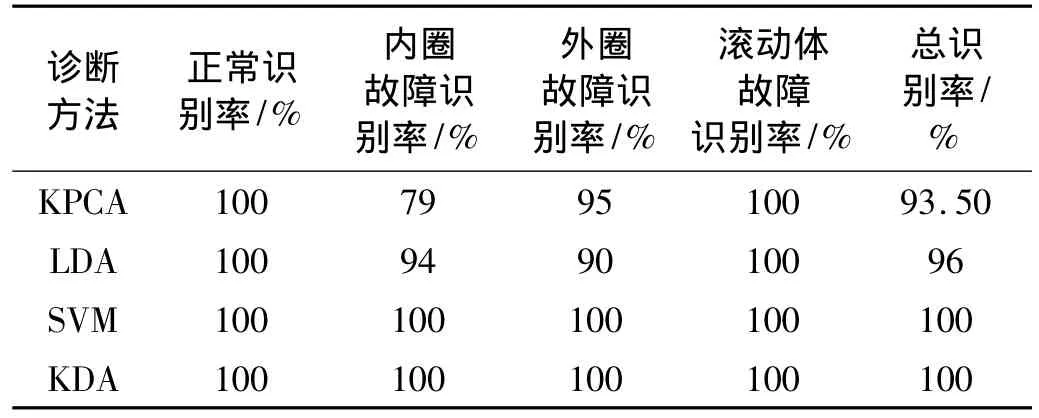
表1 基于时域特征的诊断结果Tab.1 Diagnosis results based on the time domain features

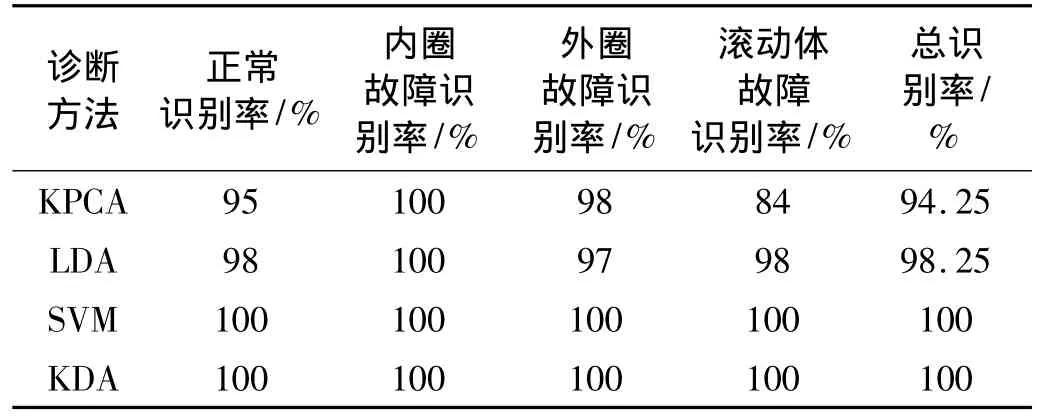
表2 基于包络谱特征的诊断结果Tab.2 Diagnosis results based on the envelope spectrum features

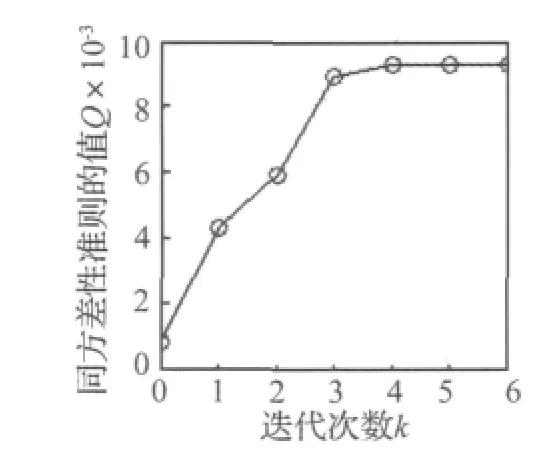
图6 同方差性准则的值随迭代次数的变化过程Fig.6 The change process of the value of homoscedastic criterion with the number of iteration

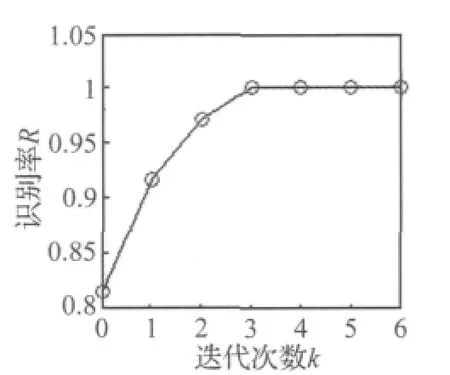
图7 识别率随迭代次数的变化过程Fig.7 The change process of the recognition rate with the number of iteration

4 结论

针对应用KDA到机械故障诊断时核参数选取困难的问题，本文提出了一种基于贝叶斯最优KDA的机械故障诊断方法。该方法通过优化同方差性准则可寻找到最优核参数，因此可有效地解决KDA中核参数的选取问题。将该方法应用于滚动轴承故障诊断，实验结果表明，该方法的故障诊断性能明显优于KPCA方法和LDA方法，与SVM方法的性能相当，而该方法可实现核参数的自动选取，因此可进一步提高故障诊断的自动化水平。

［1］Muller K R，Mika S，Ratsch G，et al.An introduction to kernel-based learning algorithms［J］.IEEE Trans.Neural Networks，2001，12(2):181 －201.

［2］袁胜发，褚福磊.支持向量机及其在机械故障诊断中的应用［J］.振动与冲击，2007，26(11):29－35.

［3］Widodo A，Yang B S.Support vector machine in machine condition monitoring and fault diagnosis［J］.Mechanical Systems and Signal Processing，2007，21(6):2560 －2574.

［4］李巍华，廖广兰，史铁林.核函数主元分析及其在齿轮故障诊断中的应用［J］.机械工程学报，2003，39(8):65 －70.

［5］胡金海，谢寿生，侯胜利，等.粗糙核主元分析方法及其在故障特征提取中的应用［J］.振动与冲击，2008，27(3):50－54.

［6］孙丽萍，陈 果，谭真臻.基于核主成分分析的小波尺度谱图像特征提取［J］.交通运输工程学报，2009，9(5):62－66.

［7］李巍华，史铁林，杨叔子.基于非线性判别分析的故障分类方法研究［J］.振动工程学报，2005，18(2):133－138.

［8］ Bo L，Wang L，Jiao L.Feature scaling for kernel fisher discriminant analysis using leave-one-out cross validation［J］.Neural Computation，2006，18(4):961 －978.

［9］Cai D，He X，Han J.Speed up kernel discriminant analysis［J］.The VLDB Journal，2011，20(1):21 －33.

［10］ Baudat G，Anouar F.Generalized discriminant analysis using a kernel approach［J］.Neural Computation，2000，12(10):2385－2404.

［11］ You D，Hamsici O C，Martinez A M.Kernel optimization in discriminant analysis［J］.IEEE Trans.Pattern Analysis and Machine Intelligence，2011，33(3):631 －638.

［12］ Mika S，Ratsch G，Weston.Fisher discriminant analysis with kernels［C］.Proceedings of the 1999 IEEE Signal Processing Society Workshop，1999:41－48.

［13］梅宏斌.滚动轴承振动监测与诊断［M］.北京:机械工业出版社，1996.

［14］ Bearing Data CenterWebsite. Case Western Reserve University［OL］.http://www.eecs.cwru.edu/laboratory/bearing.

［15］褚福磊，彭志科，冯志鹏，等.机械故障诊断中的现代信号处理方法［M］.北京:科学出版社，2009.