基于直觉模糊距离法的堰塞湖减灾方案选优*

2012-09-08王绍玉黄星

灾害学 2012年4期

关键词：文家堰塞湖直觉

王绍玉，黄星

(1.哈尔滨工业大学管理学院，黑龙江哈尔滨150001;2.哈尔滨工业大学建筑学院，黑龙江哈尔滨150001)

基于直觉模糊距离法的堰塞湖减灾方案选优*

王绍玉1，2，黄星1

(1.哈尔滨工业大学管理学院，黑龙江哈尔滨150001;2.哈尔滨工业大学建筑学院，黑龙江哈尔滨150001)

针对堰塞湖减灾群决策信息的不确定性与模糊性，为解决不完全信息条件下属性指标及专家之间存在的相互关联群决策问题，综合运用直觉模糊集理论、海明距离原理和熵权理论，将直觉模糊距离群决策方法运用到堰塞湖减灾决策过程中。工程实例研究表明，运用直觉模糊距离法决策出的最优方案具有较高的区分度和敏感性，增强了决策的客观性、科学性，能为堰塞湖减灾决策提供更为可靠的依据，具有较强的实用价值。

直觉模糊距离;堰塞湖减灾;群决策;敏感性分析

0 引言

堰塞湖减灾决策往往是在信息不完全、时间紧迫的情况下进行的，若决策失误，势必造成严重损失［1］，这意味着决策者将面临决策风险的巨大压力，会加大决策失误的概率;同时，在紧急状态下，单个决策者不可能具备解决问题的所有经验和知识，这就要求决策过程需要多个决策者共同参与才可能保证堰塞湖减灾决策的准确和安全。因此，堰塞湖减灾决策本质上是多个专家共同参与的群决策问题。

群决策为多个决策者关于方案集合中方案的偏好按某种规则集结为群体决策的一致或妥协的群体偏好序［2］。目前，国内外群决策研究众多，在研究方法上主要集中在决策者偏好的信息描述与集结上。然而，在堰塞湖减灾方案选择过程中，会出现各位专家偏好不同和备选方案评判不完全一致的问题。如何有效地将专家个人意见，通过科学的评价方法集结为群体的一致性意见，是众多群决策研究者关注的问题。为此，本文把直觉模糊距离法引入到堰塞湖减灾方案选优决策中，该方法用一个三元组(tA(x)，fA(x)，πA(x))表示决策者对某一事物的支持、反对和弃权三方面信息，使得决策者在处理不确定信息时比传统的模糊集有更强的表现力，适宜用来解决堰塞湖应急初期信息不确定条件下的紧急决策问题。该方法能够在应急状态下很好地集中专家智慧，较为准确地对备选方案建立直觉模糊评价矩阵，并利用海明距离原理将个人意见集结成能反映专家群体的一致性意见。工程实例表明，直觉模糊距离法在堰塞湖减灾方案选优决策中有较高的实用性，其敏感性分析也证明该模型和算法具有较高的区分度，能较好地保证应急决策结果的准确和可靠。

1 直觉模糊距离群决策原理

1.1 直觉模糊距离简介

堰塞湖减灾方案选优属于多属性群决策问题，本质上是集结专家个人意见为群体意见的过程，并根据专家群意见的一致度决策出最优的方案［3－4］。1986年，Atanassov对模糊集进行拓展，提出了直觉模糊集的概念，其基本定义为:设X为非空经典集合，X=(x1，x2，…，xn)，X上形如A={(x，tA(x)，fA(x)|x∈X}的三重组称为X上的一个直觉模糊集，其中，tA(x)∶X→［0，1］和fA(x)∶X→［0，1］均为X上的隶属函数，分别表示X上元素x属于A的隶属度函数和非隶属度函数，且对于A上的所有x∈X，满足:

对于直觉模糊集A:

为A中x的直觉指数。式中，tA(x)表示支持x∈A的证据的隶属度下界，称为直觉模糊集A的真隶属函数;fA(x)表示反对x∈A的证据的隶属度下界，称为直觉模糊集A的假隶属函数;πA(x)为直觉模糊集A的不确定度，是x相对于A的未知信息的一种度量。

1.2 模型构建

当专家两两之间对方案i的意见完全一致时，设其直觉模糊距离为0;当专家两两之间对方案i的意见完全相反时，设其直觉模糊距离为1;当专家两两之间对方案i的意见不全一致时，设其直觉模糊距离为［0，1］中的某个值［5－7］。根据实际情况，结合每位专家的经验及个人偏好，第k位专家对方案i的第j个评价准则或指标作出的模糊评价为则可得第k位专家对备选方案集A的模糊评价偏好矩阵为:

此距离反映了每一对专家(k，t)间对备选方案i意见的一致度。

如果所有专家两两之间一致度测量完毕，则可构造出备选方案i(i=1，2，…，r)的意见一致度矩阵(AM)，它表示m位专家两两间对备选方案i意见的一致性程度。

对评价准则{c1，c2，…，cn}的权重w={w1， w2，…，wn}的确定，因灾害环境一般较为复杂，众多信息很难及时获取，只能依靠专家经验赋予各属性指标的权重，可采取Delphi法，通过计算程序快速实现。具体方法是组织m个专家，每个专家给出一组属性权重:。对m个专家给出的权重值进行平均，得到权重均值:

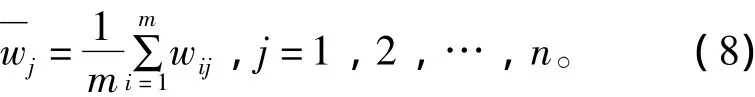
计算出每位专家所给权重与均值之间的偏差:

对偏差Δij较大的第j个属性，再请第i个专家重新估计权重wij。重复上述过程，直到偏差满足一定要求为止，并将最后得到的权重均值w={w1，w2，…，wn}作为属性的权重。

1.3 评价函数

堰塞湖减灾方案选优的评价函数，主要是综合每位专家的相对重要权重及对备选方案意见的相对一致度，得到所有专家备选方案i(i=1，2，…，r)意见的最终综合一致度为:

按照由小到大的顺序排列ei的值，值最小的方案表示专家群体对此方案评价意见的一致性程度要高，专家之间的意见分歧不大。

1.4 熵值法确定专家权重

在信息论中，熵是度量不确定性的一个指标。信息量越大，不确定性就越小，熵也越小。反之，信息量越小，不确定性越大，熵也越大［8－10］。堰塞湖减灾方案选优对专家群体的要求很高，是减灾方案决策前的重要工作。一般来讲，专家权威性越高其决策结果越可靠。因此，确定专家的权重十分重要，有必要通过一系列量化指标予以客观、公正地测度。

设专家集合Q={q1，q2，…，qk}，评价指标集B={B1，B2，…，Bn}，指标属性值L={1，2，…，n}，设满足各理想指标的理想专家的评价向量X*={1，1，1，1，1，1}，根据评价指标量值构建专家信息矩阵为:

式中:xij表示第i个专家在第j个指标的属性值，其值越小越好，属于成本型指标。

①对信息矩阵M=(xij)m×k用线性比例变换法做标准化处理，得到标准化矩阵Y=(yij)m×k，并进行归一化处理，得:

③每位专家的选择熵－Hk为:

④对专家选择熵大小进行比较，得到专家的优劣次序，根据优劣次序对每位专家赋予相对比较权重rk。则每位专家最终的相对重要权重为

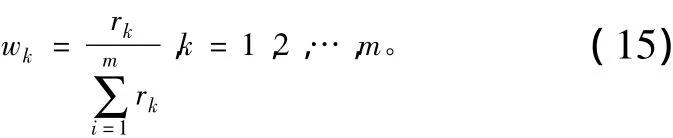
1.5 敏感度分析

从决策结果可知，对集结以后计算每个方案的ei值，并按从小到大顺序排列，ei最小为最优方案。从以上模型可知，群决策者采取直觉模糊距离模型对堰塞湖减灾方案进行评价和判断，其目的是选出最优方案，这就要求最优方案的ei值与其他方案有较大差异，才能保证决策模型和算法具有很好的敏感度，保证最优方案的可靠和正确，很显然敏感性越大，所用决策模型和算法对方案的决策效果就越好［11－12］。

假设某模型以最终决策系数ηi对决策方案进行评价，若决策系数以ηi越大越好(越小越好的情况，可用1/ηi表示)，本文以ηi越小越好来评价方案，若以max(1/η)为决策系数中最大值，次最大值为sec(1/η)，则定义方案的敏感度为:

2 堰塞湖减灾工程实例

2.1 工程概况

四川省平武县南坝镇是汶川8.0级地震的重灾区，文家坝堰塞湖位于南坝镇的涪江左岸一级支流石坎河上游，距南坝镇5 km，堰塞坝主要由石坎河左岸崩塌的覆盖层和大粒径块石组成，结构松散，多处渗水，堰塞湖基本情况如表1所示。2008年5月23日，湖内水深已达20.5 m，距坝顶仅10 m。石坎河为高山峡谷型河流，两岸山体陡峭，湖水上涨较快，平均每天上涨约0.8 m，据此推算，距漫顶仅13 d时间，而距文家坝上游约13.5 km的马鞍石还有一个较大的堰塞湖，若文家坝以上发生降雨或马鞍石堰塞湖发生溃坝，文家坝堰塞湖将提前漫顶溢流。因汶川地震的破坏，通往南坝镇的交通主干道全部中断，大型设备运不进去，给堰塞湖除险带来极大困难，仅有一条乡村公路可从江油到南坝镇，但只能通过轻型车辆，南坝镇几乎成为一座孤岛;而南坝镇又安置了数万灾民，驻有大批救灾部队和抢险人员，存放了大量的救灾物资;文家坝堰塞湖一旦发生溃坝，将严重威胁下游仅5 km的南坝镇受灾群众和抢险人员的安全，因此文家坝堰塞湖的排险施工显得异常急迫。

2.2 堰塞湖应急治理群决策

2.2.1 决策方案

由于堰塞湖上游两岸均为高山，没有过水通道，且交通中断，施工设备无法到达现场，只能在堰塞体上开挖明渠导流，以快速降低水位。测量资料显示堰塞体表面形状极不规则，总体上左高右低，中间局部形成沟底，横向有数条高差10 m左右的隆起带，纵向没有一条完整的沟状地形。根据现有施工条件和现场环境，专家集中研究了导流明渠的开挖线路，对拟开挖的导流明渠断面按石坎河发生50年一遇洪水，上游马鞍石按1/3溃坝计算溃坝洪水为2 070 m3/s，叠加马鞍石和文家坝区间洪水流量780 m3/s(50年一遇)后为2 850 m3/s，最后提出2个文家坝堰塞湖应急排险可行方案(表2，表3)。

表1 文家坝堰塞湖基本情况

表2 文家坝堰塞湖应急排险可行方案

表3 文家坝堰塞湖应急排险可行方案

2.2.2权重及评价准则

通过对专家的筛选，最终由3位专家E=(e1，e2，e3)组成群决策团体，并按熵值法求出3位专家的权重向量wk=(0.46，0.20，0.34)，通过对备选方案C=(c1，c2)众多评价准则的比较，最终确定4个关键评价指标α=(α1，α2，α3，α4)，并按Delphi法确定各准则权重(表4)。

表4 文家坝堰塞湖施工方案评价准则及权重

2.2.3 方案选优

根据评价准则，3位专家对备选方案C=(c1，c2)的直觉模糊评价偏好矩阵分别如下:

根据三位专家对备选方案的直觉模糊评价矩阵，计算专家两两(k.t)对方案C=(c1，c2)的直觉模糊距离lk，t1，lk，t2为:

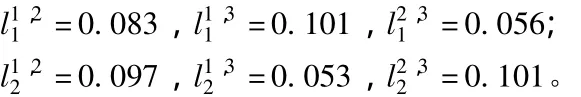
则专家E=(e1，e2，e3)对备选方案的一致度矩阵分别为:对方案c1，每位专家的平均一致度分别为:

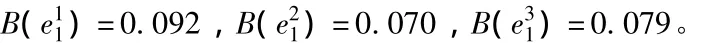
每位专家的相对一致度分别为:

三位专家评价的综合一致度为:

同理，可得方案c2的综合一致度为e2=0.08。

2.3 方案的敏感度

根据上面计算的综合一致度e1，e2，由式(16)计算本文算法的敏感度:

同时，计算文献［3，13］所述算法的敏感度(表5)。从表5可以看出，本文所采取的直觉模糊距离

表5 模型算法的敏感度比较

［1］周宏伟，杨兴国．地震堰塞湖排险技术与治理保护［J］．四川大学学报，2009(3):97－101．

［2］谭春桥，张强．基于直觉模糊距离的群决策专家意见聚合分析［J］．数学的实践与认识，2009(2):119－124.

［3］Cui Peng，Zhu Yingyan，Han Yongshun，et al．The 12 May Wenchuan earthquake-induced landslide lakes:distribution and prelinary risk evaluation［J］．Landslides，2009(6):209－223．

［4］刘宁．唐家山堰塞湖应急处置与减灾管理工程［J］．中国工程科学，2008(10):67－72．

［5］Choo E U，Wedley W C．A common framework for deriving preference values from pair wise comparison matrices［J］．Computer＆Operations Research，2004，1:893－908．

［6］Fan ZP，Xiao SH，Hu GF．An optimization method for in-tegrating two kinds of preference information in group decision-making［J］．Computers＆Industrial Engineering，2004，46:329－335．

［7］胡强，佘成学．仙岭水库土坝渗流稳定分析及除险加固措施［J］．岩土力学，2004，25(3):168－171．

［8］Ghobadi MH，Khanlari GR．Seepaproblems in the right abutment of the Shahid Abbaspour dasouthern Iran［J］．Engineering Geology，2005，82(2):119－12

［9］Chai JR，Li SY．Analysis of seepage through dam foundation with closed system of grouting curtain，drainage and pump measures［C］//Wieland M，Ren Q W，Tan JS Y．Proceeing of the 4th International Conference on Dam Engineering-Developments in Dam Engineering．London:Taylor＆Franc Group，2004:171－175．

［10］Sedat T．Treatment of the seepage problems at the Kalecik Da (Turkey)［J］．Engineering Geology，2003，68(3/4):159－169．

［11］Chen SJ，Chen SM，A new method for handing fuzzy decision making problems using FN-IOWA operators［J］．Cyernetics and Systems，2003(34):109－137．

［12］王国全，李鹏．水利工程施工方案选择的改进灰色关联分析法［J］．人民长江，2010(1):46－48．

算法，大大提高了模型的敏感度，从而保证备选方案决策结果的准确和安全。

3 结论

本文根据堰塞湖应急处置的紧迫性特点，同时考虑堰塞湖决策方案评价指标信息的不完全性以及施工现场的复杂性，综合运用直觉模糊距离法、评价准则权重确定的Delphi法以及专家权重确定的熵值法，通过模型敏感性分析，该模型提高了堰塞湖应急处置方案决策的准确性。

(1)在信息缺失条件下，采用直觉模糊距离群决策模型，能在紧急情况下迅速集结专家个体意见为群体的一致性意见，摆脱在数据严重缺乏情况下方案选优结果的不准确性。

(2)提出区分最优方案区分度敏感性分析方法。综合了决策方案与评价结果综合一致度量值之间的相互关系，较准确反映出各决策方案之间的差异，使决策结果更加真实可信。

(3)实例应用结果表明，本文所采用直觉模糊距离模型能成功地应用于类似堰塞湖应急方案的优选，决策灵敏度高，实现简便且易于计算机程序化决策，具有较强的应用价值。

Excellent Selection for Barrier Lakes Disaster Relief Schemes Based on Intuitionist Fuzzy Method

Wang Shaoyu1，2and Huang Xing1
(1．School of Management，Harbin Institute of Technology University，Harbin 150001，China;2．School of Architecture，Harbin Institute of Technology University，Harbin 150001，China)

According to the uncertainty and fuzzy of group decision information of barrier lake disaster relief，and in order to solve the correlation between the indicators and group decision experts under the condition of incomplete information，intuitionist fuzzy sets theory，Harming distance principle and entropy theory are comprehensively applied to solve the problems of barrier lake disaster relief decision in the decision-making process．Cases show that intuitionist fuzzy distance methods have a higher degree of differentiation and sensitivity and enhance the objectivity，science of the decision-making，the model can provide reliable bases for the barrier lake disaster relief decision-making and has a strong practical value．

intuitionist fuzzy distances;barrier lake disaster relief;group decision;sensitivity analysis

TU47

1000－811X(2012)04－0051－05

2012－04－25

2012－05－29

国家自然科学基金资助项目(70671033)

王绍玉(1956－)，男，河北唐山人，教授，博士生导师，主要从事城市公共安全规划与风险管理、区域发展战略规划研究．E-mail:wsy@heut.edu.cn

黄星(1979－)，男，四川南充人，博士研究生，主要从事应急供应链管理研究．E-mail:huangxing6213@126.com