基于因子分析和BP神经网络的滑坡抗剪强度参数取值*

汤罗圣，殷坤龙，刘艺梁

(中国地质大学(武汉)工程学院，湖北武汉430074)

基于因子分析和BP神经网络的滑坡抗剪强度参数取值*

汤罗圣，殷坤龙，刘艺梁

(中国地质大学(武汉)工程学院，湖北武汉430074)

滑坡抗剪强度参数取值是一直困扰滑坡防治工程设计的一大难题，目前其研究方法主要有试验法、反分析和统计分析法，但都没有考虑其他基本物理力学参数的影响。为此，提出了以某一区域工程地质条件相似的滑坡基本物理力学参数为基础，采用SPSS数学分析软件分析滑坡各基本物理力学参数与抗剪强度的相关性，筛选出对滑坡抗剪强度影响较大的因子;然后采用BP神经网络模型研究区域滑坡抗剪强度与影响因子的网络结构，并以建立的神经网络结构对该区域的滑坡抗剪强度参数进行估算;最后以万州区滑坡为例进行分析和验证。研究结果表明，采用神经网络计算的结果与滑坡试验得到的结果误差基本都在5%左右，精度较高。

因子分析;BP神经网络;抗剪强度参数;重庆万州区

滑坡抗剪强度参数是滑坡防治工程设计的基础，其研究方法目前主要有试验法、反分析、统计分析三种方法。

室内试验研究的成果很多。张芳枝等［1］、米海珍等［2］通过静三轴试验等对土体在长期浸水软化后的强度变化规律进行了探讨。程圣国等［3］通过对千将坪滑坡原位直剪试验研究，得到了滑坡原位直剪试验合理试样尺寸大小、原位直剪试验数据物理力学意义及与试验点选择部位之间的关系。王周萼等［4］在室内、外试验的基础上，通过对比室内、外试验成果，剔除异常值，综合考虑物质组成、含水量以及试验方法对抗剪强度的影响等各种因素，得到了大园包崩滑体滑带土的抗剪强度指标。

关于抗剪强度参数反分析的研究更多。郑明新［5］通过分析滑坡不同发育阶段及不同滑带部位滑带土的强度特征，论述目前使用的滑带土强度反算法的基本原理和适用条件，并提出了结合滑坡状态来综合确定滑带土强度的修正方法。程嫒彩等［6］运用最小二乘法理论，采用多个剖面和不同滑动段两种方法反算对工程实例进行分析，研究结果表明，简单小型滑坡治理设计计算中采用多个剖面反算精度较为可靠的，而在大中型复杂滑坡治理设计计算中采用不同滑动段反算更为合理。詹良通等［7］通过对国内某大型填埋场边坡失稳过程的坡面水平位移、深层侧向位移和渗滤液水位监测数据分析，开展堆体边坡稳定性反分析工作，探讨复合衬垫系统界面抗剪强度取值方法。卢坤林等［8］采用稳定性调查方法，在确定滑坡的安全系数与三维滑面的几何尺寸的基础上，通过对滑面正应力进行合理假定与修正，建立了确定滑带土抗剪强度参数的三维反分析模型。

而运用统计分析来计算抗剪强度参数主要是为了确定其随时间和地点不同的分布形式，为滑坡的可靠性评价提供参数依据。罗冲等［9］通过对三峡库区万州区几十处滑坡勘察、设计和施工资料进行统计分析，采用χ2检验法进行拟合，得到万州区滑坡抗剪强度参数c值服从对数正态分布，φ值服从正态分布。夏元友等［10］采用随机统计法和随机－模糊法对碎石粉质黏土滑带土的试验数据进行统计分析，得到祥临公路沿线该类滑带土的抗剪强度指标的概率密度函数，并对某处典型滑坡采用传统法、正交变换法、经验概率拟合法、随机－模糊法4种不同统计方法进行具体分析，研究结果表明随机－模糊法得到的c、φ值其变异系数略小于其他3种方法。袁晓蕾［11］通过对9个地区32组黄土滑坡滑带土抗剪强度粘聚力、内摩擦角直快剪、残剪、饱和固结快剪和固结快剪四种试验结果进行统计分析，结果表明c、φ的均值、标准差和变异系数具有明显的区域性特点，且具多分布属性，对正态分布、对数正态分布及极值I型分布符合都较好。李远耀等［12］通过采用地质分析和工程地质类比法将三峡库区划分为5类易滑地层，并运用K-S有限比较法，对3 308组抗剪强度参数试验数据分类进行了拟合优度检验，发现5类易滑地层中滑坡滑带土的c、φ值一般均能接受正态和对数正态分布，但c值与φ值相比，最优分布服从对数正态分布者更多，而服从正态分布者更少。

以上研究方法基本都是从滑坡抗剪强度本身的角度进行研究，而没有从影响滑坡抗剪强度参数的其他基本物理力学参数的角度进行研究。为此，本文提出了以某一区域工程地质条件相似的滑坡基本物理力学参数为基础，采用SPSS数学分析软件分析滑坡各基本物理力学参数与抗剪强度的相关性，筛选出对滑坡抗剪强度影响较大的因子，然后采用BP神经网络模型研究区域滑坡抗剪强度与影响因子的网络结构，并以建立的神经网络结构对该区域的滑坡抗剪强度参数进行估算，最后以万州区滑坡为例进行分析和验证。

1 BP神经网络模型简介

BP(Back Propagation)网络是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一［13］。图1为BP神经网络结构示意图。BP网络能学习和存贮大量的输入－输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)［13］。

其具体计算主要包括8步。

第1步:确定网络结构:根据样本数据确定输入层、隐含层以及输出层的神经元节点数。

第2步:网络初始化:初始化输入层与隐含层、隐含层与输出层之间的网络连接权重，初始化隐含层与输出层的网络阀值，制定学习速率和激励函数。

第3部:计算隐含层输出:根据输入向量、输出层和隐含层的连接权值以及隐含层阀值计算隐含层输出值。

第4步:计算输出层输出。

第5步:计算误差。

第6步:重新计算权值。

第7步:重新计算阀值。

第8步:判断是不是满足误差要求，如果不满足就返回第三步计算直到满足误差要求终止计算。

其计算的关键参数主要包括:隐含层中神经元个数的确定、传递函数的选择、训练函数的选择等。

图1 BP神经网络结构示意图

2 万州区滑坡抗剪强度参数影响因子分析

本文选取重庆万州区具有工程地质条件相似、滑带土物质岩性相同共约20个滑坡不同部位共147个滑带土样的基本物理力学参数为研究对象，采用SPSS数学分析软件研究了天然含水率、密度、比重、饱和度、孔隙率、孔隙比、液限、塑性、液性指数、塑性指数、压缩模量、压缩系数与滑坡抗剪强度的相关性，由于篇幅有限，这里仅介绍这些基本物理力学参数与天然峰值抗剪强度的相关性，具体见表1。

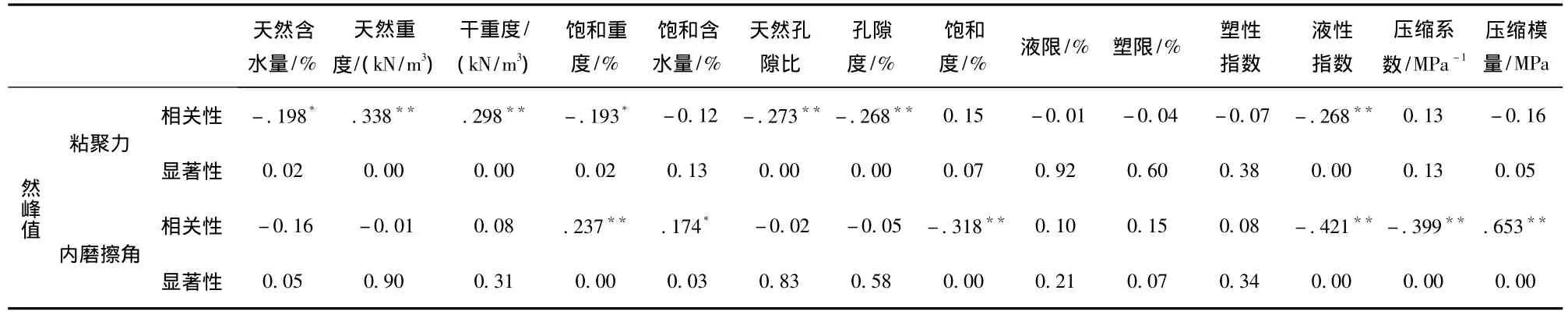
表1 滑坡天然峰值抗剪强度影响因子分析表

从表1可知，天然重度、饱和重度、天然孔隙比、孔隙度和液性指数与天然峰值粘聚力的显著性为0，说明其与天然峰值粘聚力完全相关，所以天然峰值粘聚力的影响因子为天然重度、饱和重度、天然孔隙比、孔隙度和液性指数;而饱和重度、饱和度、液性指数、压缩系数和压缩模量与天然峰值内摩擦角显著性为0，说明其与天然峰值内摩擦角完全相关，所以天然峰值内摩擦角的影响因子为饱和重度、饱和度、液性指数、压缩系数和压缩模量。

3 重庆万州区滑坡抗剪强度参数估算

3.1 样本数据选取

对于天然峰值粘聚力，根据前述研究成果可知，其影响因子为天然重度、饱和重度、天然孔隙比、孔隙度和液性指数，所以对于估算天然峰值粘聚力的神经网络，其样本数据为万州区具有工程地质条件相似、滑带土物质岩性相同共约20个滑坡不同部位共147个滑带土样的影响因子参数值。

对于天然峰值内摩擦角，同理其样本数据选取万州区具有工程地质条件相似、滑带土物质岩性相同共约20个滑坡不同部位共147个滑带土样的饱和重度、饱和度、液性指数、压缩系数和压缩模量参数值，滑坡具体情况如表2所示。

表220 个滑坡基本情况一览表

从表2可知，所选取训练样本20个滑坡都具有一个基本的特征，即滑坡分布基本都在万州区城区附近;均为堆积层滑坡，滑动面为岩土接触面;滑体为崩坡积粉质粘土夹碎块石，局部为第四系人工素填土;滑带为粉质粘土、粘土夹砂泥岩角砾;滑床为侏罗系中、上统砂、泥岩。

由于数据太多，对于147个样本的具体数据这里不宜一一列出。鉴于各数据离散性较大，为了使训练网络能够收敛，这里对输入数据和输出数据均采用了归一化处理。

3.2 BP神经网络建立

对于天然峰值粘聚力和天然峰值内摩擦角，本文均选取DPS数据处理系统的BP神经网络子系统，通过不断调试，最终选取的BP神经网络模型均是:输入层为5个输入节点，输出层为1个输出节点，隐含层15个节点，传递函数和训练函数为: logsig、purelin和trainlm。

3.3 BP神经网络的训练

(1)对于天然峰值粘聚力，所建立的神经网络训练设定:

最大训练次数10 000步;

最小训练速率为0.1;

允许误差为0.001;

学习率为0.05;

SIGMOID参数为0.9。

(2)对于天然峰值内摩擦角，所建立的神经网络训练设定:

最大训练次数100 000步;

最小训练速率为0.1;

允许误差为0.000 1;

学习率为0.05;

SIGMOID参数为0.9。

3.4 BP神经网络结果检验

天然峰值粘聚力和天然峰值内摩擦角所建神经网络采用的检验数据分别如表3、表4所示。

表3 天然峰值粘聚力检验数据

表4 天然峰值内摩擦角检验数据

根据前述建立的神经网络模型，采用其检验数据分别对天然峰值粘聚力和天然峰值内摩擦角进行估算，其结果如图2、图3所示。

其详细数据如表5所示。从表5可知，天然峰值粘聚力的绝对误差在0.19～1.70 kPa之间，其相对误差在0.63%～5.40%之间;天然峰值内摩擦角的绝对误差在0.01°～0.47°之间，其相对误差在0.05%～3.43%之间。

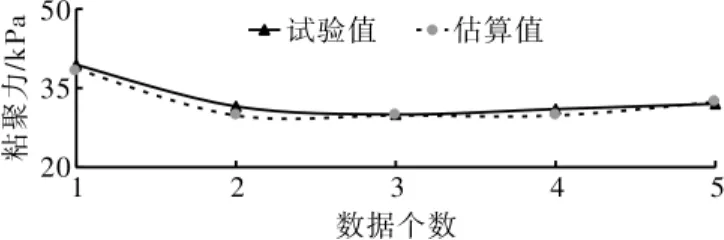
图2 天然峰值粘聚力检验结果对比

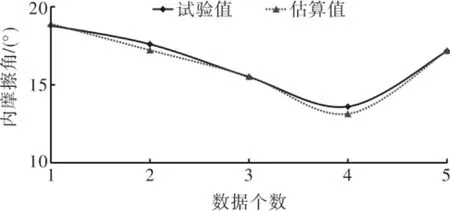
图3 天然峰值内摩擦角检验结果对比

表5 BP神经网络检验结果

4 结论

从以上研究过程，可得到以下结论。

(1)从统计学的角度可知，万州区滑坡滑带土的天然峰值粘聚力的影响因子为天然重度、饱和重度、天然孔隙比、孔隙度和液性指数，天然峰值内摩擦角的影响因子为饱和重度、饱和度、液性指数、压缩系数和压缩模量。

(2)天然峰值粘聚力和天然峰值内摩擦角所建BP神经网络模型均为:输入层为5个输入节点，输出层为1个输出节点，隐含层15个节点，传递函数和训练函数为:logsig、purelin和trainlm。

(3)经检验，所建BP神经网络结构计算结果与室内试验值相比:天然峰值粘聚力的绝对误差在0.19～1.70 kPa之间，其相对误差在0.63%～5.40%之间;天然峰值内摩擦角的绝对误差在0.01°～0.47°之间，其相对误差在0.05%～3.43%之间。无论是天然峰值粘聚力还是天然峰值内摩擦角，其误差基本都在5%左右，估算精度较高。

(4)从统计学的角度首先筛选滑坡抗剪强度的影响因子，然后以影响因子参数数据为训练样本，采用BP神经网络来估算滑坡的抗剪强度参数，经检验能够达到估算精度要求，为滑坡抗剪强度参数选取提供了一种新的思路。

［1］张芳枝，陈晓平，吴煌峰，等．东深供水工程风化泥质软岩残余强度特性研究［J］．工程地质学报，2003，11(1):54－57.

［2］米海珍，王昊，高春，等．灰土的浸水强度及残余强度的试验研究［J］．岩土力学，2010，31(9):2781－2785.

［3］程圣国，傅又群，罗先启．滑坡滑带土原位直剪试验应用研究［J］．路基工程，2008(2):10－11．

［4］王周萼，栾约生．大园包崩滑体滑带土抗剪强度指标研究［J］．资源环境与工程，2009，23(S2):126－128，141.

［5］郑明新．论滑带土强度特征及强度参数的反算法［J］．岩土力学，2003，24(4):528－532．

［6］程嫒彩，戴自航．多剖面反算滑带土抗剪强度指标的研究［J］．岩土力学，2006，27(10):1811－1814．

［7］詹良通，管仁秋，陈云敏，等．某填埋场垃圾堆体边坡失稳过程监测与反分析［J］．岩石力学与工程学报，2010，29(8): 1697－1705．

［8］卢坤林，朱大勇，许强，等．滑带土抗剪强度参数的三维反分析［J］．岩土力学，2010，31(10):3319－3323．

［9］罗冲，殷坤龙，陈丽霞，等．万州区滑坡滑带土抗剪强度参数概率分布拟合及其优化［J］．岩石力学与工程学报，2005，24 (9):1588－1593．

［10］夏元友，蒋超．云南祥临公路滑坡滑带土抗剪强度指标的统计分析［J］．岩土力学，2006，27(6):920－924．

［11］袁晓蕾．黄土滑坡的滑带土强度试验参数统计及可靠性研究［D］．西安:长安大学，2007．

［12］李远耀，殷坤龙，柴波，等．三峡库区滑带土抗剪强度参数的统计规律研究［J］．岩土力学，2008，29(5):1419－1424．

［13］孙伟娟．神经网络理论与实现［M］．北京:电子工业出版社，2007.

Parameter Value Selection on Anti-shearing Strength Parameters of Landslides Based on Factor Analysis and BP Neural Network

Tang Luosheng，Yin Kunlong and Liu Yiliang
(Engineering Faculty，China University of Geosciences(Wuhan)，Wuhan 430074，China)

Parameter value selection on anti-shearing strength parameters of landslides，which had been being a difficulty in landslide prevention and control engineering design，is presently studied mainly by test，back analysis and statistical analysis without considering the influence of other basic physical and mechanical parameters．By using a method based on basic physical and mechanical parameters of landslides，which have similar engineering geological conditions in an area，the correlation between basic landslide physical and mechanical parameters and anti-shearing strength are analyzed by adopting mathematical analysis software SPSS，factors with greater influence are screened．Then，BP neural network model is used to establish a neural network structure between the antishearing strength and influence factors in the research area，which is applied to estimate the landslide anti-shearing strength parameters of this region．Finally，the accuracy is analyzed and verified by taking Wanzhou landslides as an example．The results show that the error between the experiment results and the calculation result using the neural network is less than 5%，and its precision is higher．

factor analysis;BP neural network;anti-shearing strength parameters;Wanzhou district in Chong Qing city

P642.2

A

1000－811X(2012)04－0017－05

2012－02－24

2012－03－30

国家自然科学基金项目(41002103);中央高校基本科研业务费专项资金优秀青年教师基金(CUGL100213)

汤罗圣(1984－)，男，湖北石首人，博士研究生，从事地质灾害机理及预测预报研究．E-mail:homeandm@163.com