均衡法评价地下水可开采量的风险率

刘佩贵，陶月赞

合肥工业大学土木与水利工程学院，合肥 230009

均衡法评价地下水可开采量的风险率

刘佩贵，陶月赞

合肥工业大学土木与水利工程学院，合肥 230009

有限数据样本量所关联的不确定性因素，对水资源评价结果的可靠度有着显著影响。在地下水源地勘查与运行过程中，地下水位变幅是一个具明显缓变性质的随机变量。以山东省济宁市承压水源地为例，利用水均衡法评价方法，基于模糊－随机模型，定量研究缓变随机变量在先验分布与后验分布条件下对评价结果的风险影响。结果表明：受不确定性因素时变特性的影响，水源地按勘查成果形成的计划开采量运行，将导致水源地形成过量开采的风险率由13.67%增加至15.75%；考虑不确定性因素时变特性影响，随机变量的不确定性区间由5.64减小到3.60；利用后验信息及时调整开采计划，可保障水源地的供水安全。

时变不确定性；贝叶斯理论；风险率；地下水；开采量；水均衡法

0 引言

地下水资源开发利用过程中存在众多的不确定性因素，依据不确定性因素的成因，可分为客观不确定性因素（主要表现在时间和空间上的不均一性）与主观不确定性因素（主要体现在水文地质参数的确定、水文地质概念模型的概化两方面）［1－3］。对上述不确定性因素，有关专家学者给予了高度重视并进行了深入研究［4－7］；现有研究文献对这些不确定性因素，基本都认为其不随水源地运行而变化。水源地运行，在对勘查与评价成果进行检验的同时，对勘查所未控制或评价所未认识的水文地质条件也将逐渐暴露；另外，勘查与评价中已明确的水文地质条件，也可能随水源地运行而产生一定变化。上述2种不确定性因素，将对勘查与评价所确定的开采计划形成影响，甚至危及到水源地的运行安全；一般而言，这2种不确定性因素，随水源地运行而被逐渐认识或确定，该过程具有明显的缓慢时变特征。定量研究这类不确定性因素对评价结果的影响，将为水源地实时调整开采计划以保证水源地安全，提供技术支撑。

水文地质概念模型，一般是以水文地质勘查为基础，对研究区水文地质条件的概化；受勘查工作量、勘探技术和手段等条件的限制，当水源地启动运行后，对水文地质条件的进一步验证工作，一般不再通过水文地质钻探来直接验证，而多依赖地下水水位长期观测进行间接验证。为此，以水源地可开采量均衡法评价成果的风险率为例，讨论水文地质参数的不确定性对风险率大小的影响。

1 不确定性因素的时变特性

中。如地表裸露或覆盖程度较差的岩溶地区，一次降雨过程，使岩溶区地下水的补给量迅速增加，泉口的出流量也随之增大，常以“天”或“月”为单位进行动态评价。

这两种时变性均将不同程度地影响到地下水水源地的供水安全，不容忽视；但这两者又是相对独立的，分析其影响程度时可分别考虑。

2 贝叶斯理论

贝叶斯（Bayes）理论是经典统计学的延伸和扩展，该方法通过综合考虑随机变量的先验信息和样本信息，得到该变量的后验分布，以此进行统计计算，从而为实现风险率的动态估算提供切实可行的方法。目前，该方法已成功应用于水文预报、水工泄洪闸门事故率分析方面［8－9］，但在地下水资源风险分析方面的研究文献较少。

2.1 贝叶斯公式

由原始基础资料得到随机变量x的样本信息为y，其先验与后验分布可以用f（x）和f（x｜y）表示，按照条件概率公式则有Bayes表达公式：

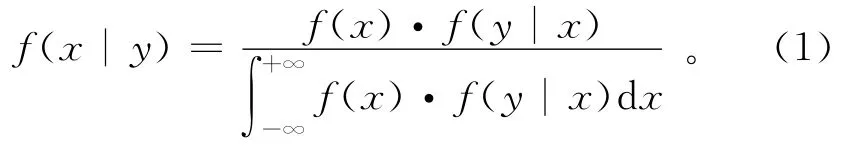
水源地的运行，会逐渐暴露出一些勘查所未控制或评价所未认识的水文地质条件，并可能诱发一些已确定的水文地质条件也产生一定程度的变化；这些不确定性因素，表现出一定的时变特性，从时间尺度上可分为“缓变性”和“陡变性”［8］。

1.1 缓变性

水源地运行过程中，受水文气象条件季节性变化、人类活动等的影响，地下水的补给量或排泄量均发生一定程度的缓慢变化。如随着城市化建设的发展，水源地所在的水文地质单元内的下垫面条件发生变化，引起地下水的水力坡度、含水层之间的水头差等要素发生变化，最终导致水源地的地下水可开采量发生变化。特别是在抽取承压含水层中的水时，若因开采产生地面沉降，则可能引起水文地质参数发生变化。该类型的时变特性，通常以“年”为单位进行动态评价。

1.2 陡变性

陡变性通常发生在一个相对较短的时间过程

式中，f（y｜x）为似然函数。

由式（1）可见，先验分布、似然函数和后验分布是贝叶斯理论的3个关键变量的分布函数，且后验分布与先验分布和样本对参数的条件分布有关，是两者的综合，即后验分布既反映了过去信息提供的先验分布，又反映了新收集的样本提供的信息，体现出一个知识综合与更新的过程。

2.2 正态过程的共轭先验分布

为解决式（1）中积分的困难，发展了“共轭先验分布”［10］；该分布要求先验分布与后验分布属于同一个类型，即要求经验的知识和现在样本的信息有某种相同的特性，它们能转化为同一类的经验知识。

地下水资源评价中涉及的随机变量主要有含水层的渗透系数K、弹性释水系数μ＊、含水层之间的水头差ΔH、越流补给系数b等。从统计学角度，其采样过程一般为连续型，它们的值可能取自然数中的任何一个数（假设不考虑参数取值所代表的地质意义），且分布一般服从正态分布，而正态分布因其特有的数学特性，在不同领域得到广泛应用。此外，文献［2，11］的研究结果表明，与参数的数字特征相

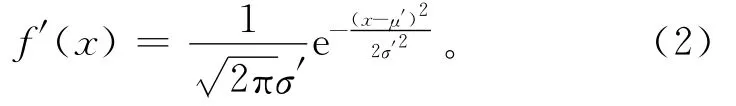
经过一段时间后，获得样本容量为n的x值，且样本均值和标准差分别为μ和σ，则x的后验密度f″（x｜y）也服从正态分布：比，参数的分布概型不是影响计算风险率大小的主要因素；因此，以随机变量服从正态分布为例，讨论正态过程的正态分布族。

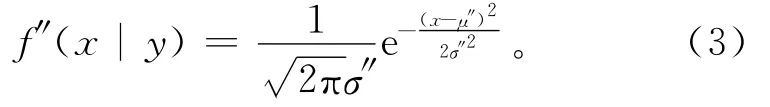
设随机变量x的先验分布f′（x）为正态分布，用μ′和σ′分别表示随机变量的均值和标准差。其密度函数为

其中，y表示样本结果。通过估计统计量，得到后验参数μ″和σ″2，以及先验分布参数、样本信息参数的关系式［12］分别为

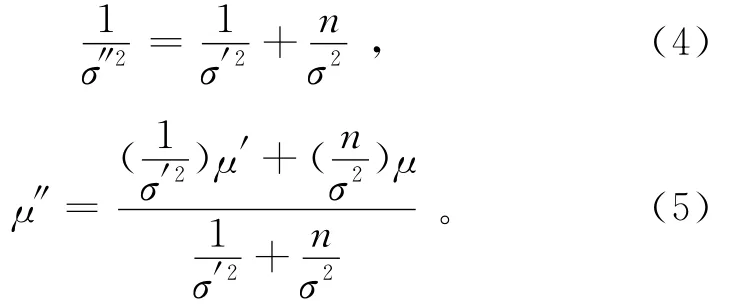
从式（4）和（5）可以看出：后验方差σ″2的倒数等于先验方差的倒数和样本方差的倒数之和，后验均值μ″则有权平均的含义，即先验均值和样本均值的权平均；而权量正是各自方差的倒数，且后验均值总是位于先验均值和样本均值之间，后验方差总是小于先验方差。

3 应用实例

3.1 研究区概况

研究区的区域地貌类型属于泰沂山前冲积平原与鲁西南黄泛平原向斜地貌，含水层主要是呈多层结构分布的第四系孔隙含水层（包括潜水和承压水）。因研究区内的地表水体污染极为严重，而区内的地表水与浅层地下水有密切的水力联系，且河水位高于浅层地下水，河水直接补给浅层地下水，造成浅层地下水遭受污染。深层承压水埋深一般在60～150m，其上分布有较稳定的黏性土，与下部基岩风化壳含水层之间有一层稳定的黏性土隔水层，岩性主要为中粗砂及砂砾石，富水性较好，水质较优。因此，为满足城市供水要求，该承压含水层确定为开采目的层。

由于区内承压水埋藏较深，且上覆有较稳定的黏性土，大气降水不能直接补给深层地下水，但部分地区可通过天窗接受浅层水的越流补给，成为其补给来源之一；另外，研究区内已形成地下水水位降落漏斗，周边的地下水以侧向径流的方式补给区内的深层地下水。综上可知，该承压含水层的补给量主要来自潜水含水层的越流补给和承压含水层本身的侧向径流补给［4］。通过对水源地水文地质条件的概化，依据可开采系数法（取系数为0.9［13］），地下水可开采量计算公式为

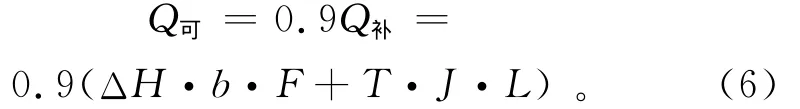
式中：Q可为地下水可开采量（m3／d）；Q补为承压含水层补给量（m3／d）；ΔH为承压含水层与潜水含水层之间的水头差（m）；b为越流补给系数（1／d）；F为计算区面积（m2）；T为承压含水层的导水系数（m2／d）；J为水力坡度；L为计算区的周长（m）。

3.2 数学模型的建立

地下水开采系统作为一个客观、开放型的复杂系统，广泛存在着不同类型的不确定性因素，从而使式（6）中的变量ΔH、T、b、J等表现出随机性、模糊性、灰色性、未确知性等方面的不确定性［14］（数字特征见表1）。为了评估多种不确定性因素对评价结果的综合影响程度，许多学者利用耦合模型以尽可能地准确反映实际条件［14］。实例研究中，利用模糊－随机数学模型［2］，估算动态风险率：

表1 模糊随机变量取值范围和数字特征Table 1 Value range and numerical characteristics of fuzzystochastic variables

3.3 随机变量的时变不确定性分析

由式（6）可以看出，Q可为ΔH、T、b、J4个随机变量的非线性函数，其中变量b和T是反映当地水文地质条件的参数。虽然在不同的地质作用如沉积、冰川、侵蚀下，可以形成不同岩性的含水层，从而导致含水层参数（如给水度、渗透系数）呈现出很大的空间变异性［15］，但从水源地的运行时间来说，一般情况下，与水头差ΔH相比，b、T的时变特性变化不明显（它们的不确定性主要来源于采样点的空间分布与样本容量），且由于人力、物力等条件的限制，不可能再增加水文地质钻探工作，也就不可能获得更多的有关随机变量b、T的样本信息，故暂不考虑随机变量b、T的样本信息。当水源地启动运行后，可以依赖地下水水位长期观测获得水头差ΔH的样本信息。因此，该实例中所讨论的时变效应，主要指水头差ΔH的“缓变性”。

由历史资料所获得的水头差ΔH的均值μΔH和标准差σΔH分别为12.5m和1.44m（表1），即为时变随机变量ΔH先验概率分布的均值和标准差μ′和σ′；此时对应的先验概率密度函数分布如图1所示。因历史资料有限，这一先验分布的假设是比较粗糙的，但又是十分必要的，它反映了潜水含水层与承压含水层的水头差分布状态。水源地在运行中通过对长观孔的观测，经过一段时间后，得到一组样本容量n＝20的有关ΔH的观测资料，样本的均值μ＝11.82m，均方差σ＝5.35m。根据公式（4）和（5）得后验均值和后验均方差分别为μ″＝12.10m，σ″＝0.92m，相应的后验概率函数分布如图1所示。对比图1中的两条曲线可以看出：后验分布曲线较先验分布变陡，先验95%的置信区间是（9.68m，15.32m），后验95%的置信区间是（10.30m，13.90 m）；也就是说，收集新的样本信息之后，95%置信区间的间距由5.64m减小到3.60m，随机变量的不确定性区间变小，数据的精密度提高，从而可以进一步提高评价结果的可靠度。

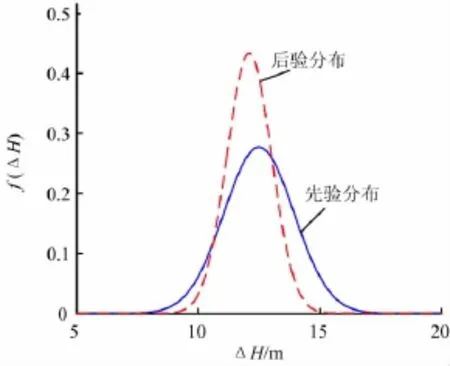
图1 随机变量的概率分布图Fig.1 Probability distribution of random variableΔH

3.4 动态风险率估算与结果分析

用改进一次二阶矩法（AFOSM）［2］计算不同截集λ情况下的模糊风险率（水源地设计开采量为12.0×104m3／d），求得先验分布与后验分布下的模糊风险率，如表2所示。综合表2和图2的数据可知：考虑样本信息后，当仅考虑参数的随机性（λ＝1.0）时，以12.0×104m3／d开采时发生地下水过量开采的风险率由9.18%增大到10.93%；同时考虑参数的模糊性和随机性时，相应的模糊风险率由13.67%增大到15.75%（取λ＝0.5时对应的模糊风险率的均值（表2中黑体字））。

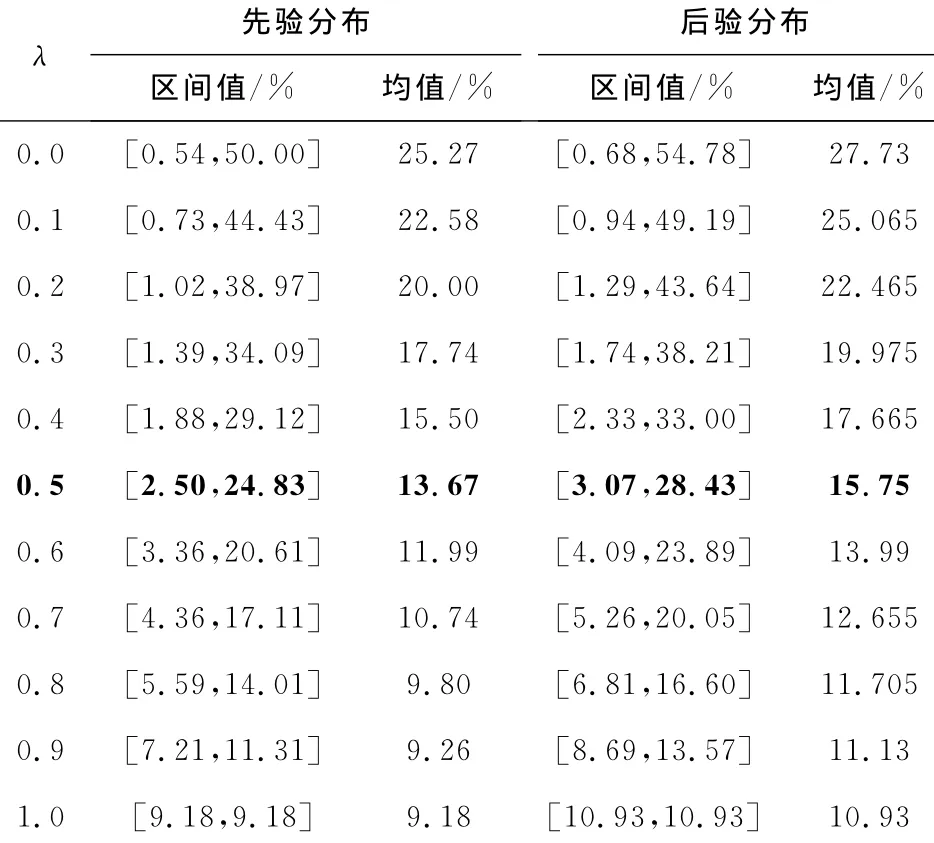
表2 模糊风险率计算结果Table 2 Calculated results of fuzzy risk

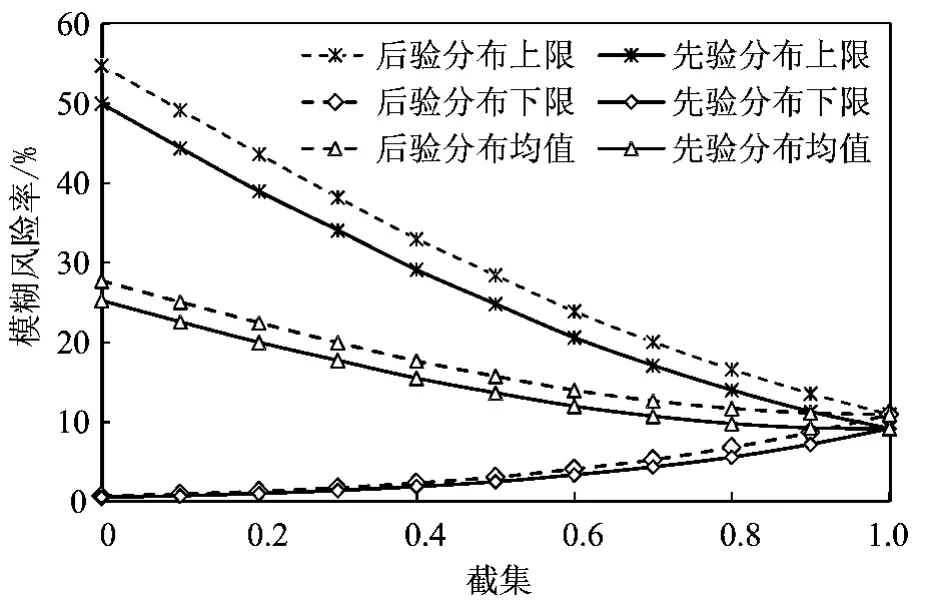
图2 先验分布与后验分布条件下的模糊风险率对比曲线Fig.2 Compared curve of fuzzy risk between prior distribution and posterior distribution

由图2可以比较直观地看出：随着λ值的增大模糊风险率区间逐渐变小，这是因为λ值越大，模糊区间越小；同一λ值，后验分布条件下得出的风险率均大于先验条件下的风险率，即随着水源地的运行，受不确定性因素时变特性的影响，风险率发生了变化。若仍按12.0×104m3／d的水量进行开采，则水源地发生地下水过量开采的风险率将增大；原因在于受人类活动及周围环境变化的影响，通过进一步观测得到样本信息中的潜水含水层与承压含水层的水头差变小，导致含水层得到的补给量相应地减少。

4 结论

水源地运行，逐渐暴露出的勘查所未控制或评价所未认识的水文地质条件，以及勘查与评价已明确的水文地质条件所发生的变化，都属时变不确定性因素；在关于这类不确定性因素对水源地运行安全影响的定量研究过程中，形成以下认识：

1）不确定性因素对水源地运行的影响，多可依据地下水水位动态来间接反映或验证；地下水动态长期监测，可为水源地风险管理提供重要基础数据。

2）后验分布既反映了过去信息提供的先验分布，又反映了新收集的样本提供的信息，后验分布与先验分布和样本对参数的条件分布有关，是两者的综合，体现出一个知识综合与更新的过程。

3）水源地以计划开采量12.0×104m3／d运行，先验分布与后验分布条件下发生地下水过量开采的模糊风险率分别为13.67%和15.75%；如能利用后验信息对开采计划进行及时调整，可提高水源地的安全运行系数。

（References）：

［1］ 束龙仓，朱元生.地下水资源评价中的不确定性因素分析［J］.水文地质工程地质，2000，27（6）：6－8.

Shu Long－cang，Zhu Yuan－sheng.Analysis of Uncertainties in Groundwater Resource Evaluation［J］.Hydrogeology and Engineering Geology，2000，27（6）：6－8.

［2］ 刘佩贵.地下水开采的风险率估算模型研究［D］.南京：河海大学，2008.

Liu Pei－gui.Risk Estimation Model and its Application on Groundwater Pumping［D］.Nanjing：Hohai University，2008.

［3］ 刘佩贵，束龙仓.傍河水源地地下水水流数值模拟的不确定性分析［J］.吉林大学学报：地球科学版，2008，38（4）：639－642.

Liu Pei－gui，Shu Long－cang.Uncertainty on Numerical Simulation of Groundwater Flow in the Riverside Well Field［J］.Journal of Jilin University：Earth Science Edition，2008，38（4）：639－642.

［4］ 束龙仓，朱元生，孙庆义，等.地下水允许开采量确定的风险分析［J］.水利学报，2000，31（3）：77－81.

Shu Long－cang，Zhu Yuan－sheng，Sun Qing－yi，et al.Risk Analysis of Groundwater Allowable Withdrawal Evaluation［J］.Journal of Hydraulic Engineering，2000，31（3）：77－81.

［5］ Baalousha H，Kongeter J.Stochastic Modeling and Risk Analysis of Groundwater Pollution Using FORM Coupled with Automatic Differentiation［J］.Advances in Water Resources.2006，29（12）：1815－1832.

［6］ Feyen L，Dessalegn A M.Applicatin of a Bayesian Approach to Stochastic Delineation of Capture Zones［J］.Ground Water，2004，42（4）：542－551.

［7］ 王威，苏小四，王小元.地下水开采下的植被生态风险评价：以鄂尔多斯乌兰淖地区为例［J］.吉林大学学报：地球科学版，2010，40（6）：1344－1352.

Wang Wei，Su Xiao－si，Wang Xiao－yuan.Vegetation Ecological Risk Assessment Research Under the Impact of Groundwater Withdraw：A Case Study of Wulannao Area，Ordos Basin［J］.Journal of Jilin University：Earth Science Edition，2010，40（6）：1344－1352.

［8］ 姜树海，范子武.Bayes方法在水工泄洪闸门事故率分析中的运用［J］.水利学报，2006，37（8）：945－949.

Jiang Shu－hai，Fan Zi－wu.Application of Bayesian Approach to Accident Rate Analysis of Outlet Gates［J］.Journal of Hydraulic Engineering，2006，37（8）：945－949.

［9］ 姜树海，范子武.基于Bayes方法的堤坝时变渗流风险率评估［J］.岩土工程学报，2007，29（3）：420－424.

Jiang Shu－hai，Fan Zi－wu.Assessment of Seepage Time－Varying Risk Rate for Embankments and Dams Based on Bayesian Aproach［J］.Chinese Journal of Geotechnical Engineering，2007，29（3）：420－424.

［10］ 张尧庭，陈汉峰.贝叶斯统计推断［M］.北京：科学出版社，1991：1－31.Zhang Yao－ting，Chen Han－feng.Bayesian Statistical Inference［M］.Beijing：Science Press，1991：1－31.

［11］ Shu L C，Liu P G.Application of M－C and JC Methods on Uncertainties Analysis in Groundwater Resources Evaluation［C］／／Proceedings of the International Symposium on Flood Forecasting and Water Resources Assessment for IAHS－PUB.Beijing：China Waterpower Press，2006：663－670.

［12］ 言茂松.贝叶斯风险决策工程［M］.北京：清华大学出版社，1989：27－68.

Yan Mao－song.Risk Decision－Making Project Based on Bayes Theory［M］.Beijing：Tsinghua University Press，1989：27－68.

［13］ 张瑞，吴林高.地下水资源评价与管理［M］.上海：同济大学出版社，1997：143－147.

Zhang Rui，Wu Lin－gao.Groundwater Resources Evaluation and Management［M］.Shanghai：Tongji University Press，1997：143－147.

［14］ 左其亭，马军霞.地下水系统中的不确定性信息及其处理方法［J］.水文地质工程地质，1994（5）：41－43.

Zuo Qi－ting，Ma Jun－xia.Uncertain Information and Its Evaluated Method of Groundwater System［J］.Hydrogeology and Engineering Geology，1994（5）：41－43.

［15］ Ganoulis Jacques G.水污染的工程风险分析［M］.彭静，廖文根，李锦秀，等译.北京：清华大学出版社，2005：131－150.

Ganoulis Jacques G.Engineering Risk Analysis of Water Pollution［M］.Translated by Peng Jing，Liao Wen－gen，Li Jin－xiu，et al.Beijing：Tsinghua University Press，2005：131－150.

Risk of Groundwater Allowable Withdrawal Evaluated Using Water Balance Method

Liu Pei－gui，Tao Yue－zan
School of Civil Engineering，Hefei University of Technology，Hefei 230009，China

Uncertain factors associated with limited samples have significant influence on the reliability of groundwater resources evaluation result.Groundwater table is a time－dependent stochastic variable during the well field exploration and operation.Therefore，take a confined aquifer of Jining City，Shandong Province as an example，the risk of prior probability distribution and posterior probability distribution are evaluated quantitatively with the fuzzy－stochastic model using Bayesian theory in this paper.The study results show that the fuzzy risk of groundwater over－drafted is increased from 13.67%to 15.75%.Considering the time－dependent uncertain factors，the uncertain interval spacing becomes smaller from 5.64to 3.60.Consequently，the pumping plan should be adjusted to guarantee the safe supply.

time－dependent uncertainty；Bayesian theory；risk；groundwater；extraction；water balance method

book=2012,ebook=608

P641.8

A

1671－5888（2012） 04－1125－05

2011－09－12

中央高校基本科研业务费专项资金项目（2011HGQC1028），合肥工业大学博士学位人员专项基金（GDBJ2009－016）

刘佩贵（1981－），女，博士，主要从事风险分析与水资源评价方面的研究，E－mail：liupg2512＠163.com。