超声声场的三维模拟及可视化研究

2012-09-06张艳花

山西电子技术 2012年5期

景妮，杨录，张艳花

（中北大学信息与通信工程学院，电子测试技术国家重点实验室，山西太原 030051）

科学计算可视化（VISC），即运用计算机图形学和图像处理技术，将科学计算过程中产生的数据及计算结果转化成图形和图像显示出来进行交互式处理的理论、方法、技术，直观的图形图像更有利于人们对于抽象数据的理解和分析。超声场的分布关系到超声成像，超声检测等多个工程实际问题，目前在这一方面的研究很多但要准确地模拟换能器发射超声波声场比较困难，超声场的三维模拟及可视化也比较困难，有待进一步的深入研究。本文利用MATLAB强大的图形可视化功能对超声场进行三维模拟可视化，能够很方便地进行交互控制和管理研究超声换能器发射声场的分布特征，掌握各变量，以及换能器各参数对声场产生的影响。

1 圆形活塞超声换能器声场的数学模型及三维图形的建立

我们要将一种物理现象（尤其是看不到、摸不到的物理现象如超声声场），通过科学计算可视化将其变成一种直观的、易于人们理解的图形图像形式通常有以下几个步骤，首先要建立一个物理模型（物理定律），然后将其转化成数学模型（数学表达式），再通过数学模型提出计算模型送入计算机计算（计算机的模拟），模拟结果数据经可视化处理转换成可视图形或图像信息，提供给人们作分析和研究。本文即按照以上步骤分别对处于标准大气压强中圆形活塞换能器的中心轴线上声压、轴向声场、声轴横截面声场进行数学建模并用MATLAB对其进行可视化模拟。

超声探头的辐射声场可以用克希霍夫积分定理描述如下:

其中Φq是声场中任意一点Q处的速度势，Φs是包围Q点曲面S上的速度势，（）为曲面S上振动速度的法向分量，k=2π/λ，r为某积分面元ds到Q点的矢量。

通过这个式子出发，我们可以推导出超声换能器声场的数学模型。

1.1 超声换能器声场中心轴线上声压分布的数学模型以及可视化图形

超声场声压p是某一点在某一瞬间的压强P1与没有超声场时的静态压强P0之差即p=P1-P0，单位Pa。

在圆形活塞表面上每一点都可视为单一点源，每一点源都以相同的振幅和相位作简谐运动，轴线上任一点处的声压只要把换能器上所有点辐射到这一点的声压叠加即可。

其中，P0为静态压强，Rs为圆形活塞半径，r为活塞中心到轴线上某一点的距离，k=2π/λ。

由上式我们不难看出声场中心轴线上的声压是随时间做周期性变化的，在工程实际应用中我们只需要考虑其幅值的情况，因此我们取其幅值即:

本文选取半径Rs为3 mm，发射频率f为40 kHz的圆形活塞，研究其超声声场中心轴线上的声压分布，通过（3）式的数学模型提出相应的计算模型，运用MATLAB强大的图形可视化功能，将抽象的声场声压转化成我们可视的图形方便我们对其进行分析应用。

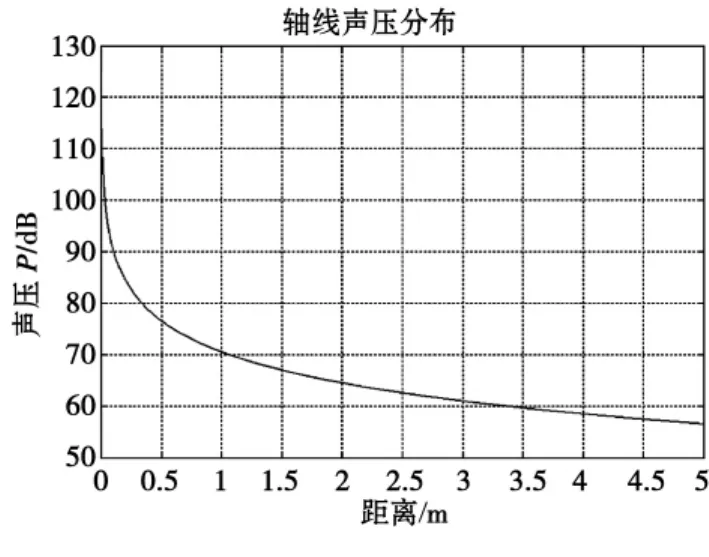
图1 为声场轴向声压分布

由于我们所选的探头参数小图形变化会比较集中，变化陡急，因此将坐标变换为以分贝作为单位，更有利于我们观察分析。同时我们能够很方便地进行交互式处理和控制，如将其活塞半径、发射频率等参数进行修改研究其声场声压特征强度。

1.2 超声换能器轴向声场声压分布的数学模型及三维可视化图形

首先我们来研究轴线外任意点的声压分布（见图1）。

图2 圆形活塞声源声场的示意图

把活塞上每个微元看成一个单一的点源，则在换能器轴向空间任一点的声压则为，活塞中所有微元到这一点源声压的叠加和。经过积分变化我们得到探头足够远（r＞3R2s/λ）处的声压:

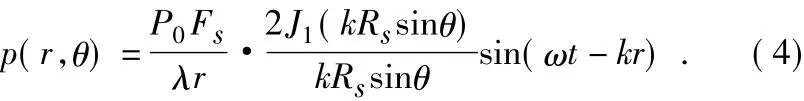
其中Fs=πR2s，为圆盘面积，J1为第一类一阶贝塞尔函数，MATLAB提供强大的函数功能，可在其函数库中直接调用。同样我们工程中只需要研究声压幅值即:

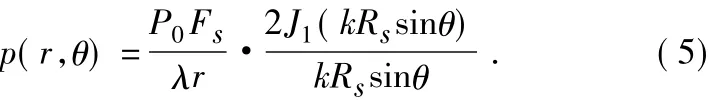
我们将上式中的球坐标变换成笛卡尔坐标系，其转化公式为:

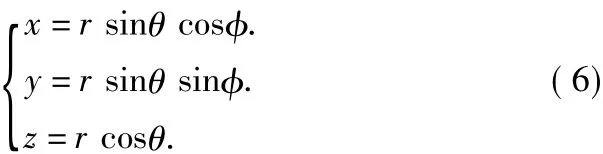
将（5）进行变化得到声轴轴向表达式:

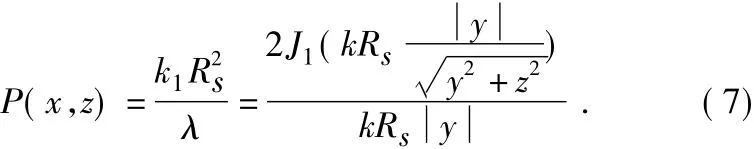
其中k1=P0π

图3为半径Rs为3 mm，发射频率f为40 kHz的，通过（7）式建立的数学模型，用MATLAB仿真出超声换能器声压分布的三维图形:

图3中第一幅图为探头轴向声场声压的三维分布图形，第二幅图为第一幅图沿垂直Z轴方向上的视图，第三幅图为第一幅图的俯视图。图中色轴坐标表示声压的大小。同样声压轴以分贝作为单位，更有利于我们研究分析。由图中我们可以看出在远场区（r＞3R2s/λ）声压逐渐变小，同时在换能器的轴线附近声压比较大。

1.3 超声换能器声轴截面声场声压分布的数学模型及三维可视化图形

我们要研究距离超声换能器一定远处平面上的声压分布情况，就需要作出该平面的声压分布图。同理我们先来研究其数学模型。由上文中（5）式和（6）式我们可以得到声轴截面声压分布的数学模型:

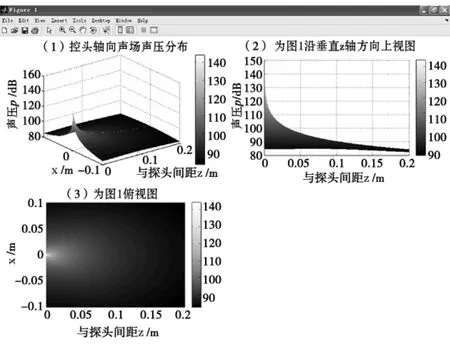
图3 超声声场轴向声压分布图

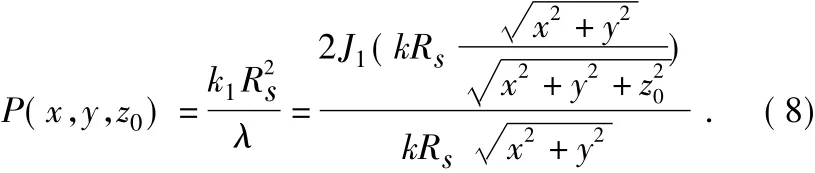
其中，z0为换能器中心到截面的距离。

图4为半径Rs为3 mm，发射频率f为40 kHz的，z0取1.1 mm，通过（8）式建立的数学模型，用MATLAB仿真出超声换能器声压分布的三维图形:

图4 声轴截面声场的声压分布

图4中第一幅图距探头z0处声轴截面声场声压分布的三维图形，第二幅图为第一幅图x轴方向的视图，第三幅图是第一幅图的俯视图。图中色轴坐标表示声压的大小。同样声压轴以分贝作为单位。由图中我们可以看出截面上声场呈轴对称分布，在中心轴线附近声压最高，轴线附近声场衰减较慢，轴线两侧声场声压呈快速振荡衰减趋势。声场的能量主要集中在轴线附近。