基于BP神经网络的地下水动态预测

张 斌，刘俊民

（西北农林科技大学 水利与建筑工程学院，陕西 杨凌712100）

地下水是贮存于地球表面松散层孔隙或基岩裂隙中的水资源，是人类不可缺少的一种宝贵的自然资源，对人类生活、工农业生产及城市建设都起着重要作用。同时，地下水也是影响生态环境系统的一个重要因子，地下水的流量大小、水位高低往往会影响生态系统的天然平衡状态。进入21世纪，随着工农业生产的迅速发展和城市化进程的不断加快，人类对水资源的需求量越来越大，相应地下水资源开发利用的规模也越来越大，相伴而来的便是愈演愈烈的不合理地下水开发而导致的一系列严重的生态环境问题。地下水水位是地下水的一个重要指标，地下水水位的变化受区域地下水系统中影响水位变化的因素所激励，即影响因素与地下水位之间存在着一种映射关系，这种映射关系一般是非线性的，而人工神经网络正是一种高度非线性的并行分布处理系统［1］。宝鸡市北临黄土台塬，南依秦岭山脉，西为群山所阻，东去进入宽阔的关中平原，呈长条状分布在渭河两岸的高漫滩及一级阶地之上，东西长20km，南北宽3～5 km。为了保护地下水资源，宝鸡市政府实施逐年关停自备井，使地下水开采量从2000年前的6 000万m3下降到目前的2 000万m3，减少了4 000万m3。地下水开采量的大幅度减少使得地下水资源得到了有效的补充与涵养。

1 BP神经网络简介

1.1 BP神经网络的基本结构

BP（Back Propagation）神经网络是一个有指导的多层前馈神经网络，由输入层、隐含层和输出层组成，每层又有若干个神经元，如图1所示，它是三层前馈神经网络的拓扑结构，其中第一层为输入节点，第二层为隐节点，第三层为输出节点［2－3］。

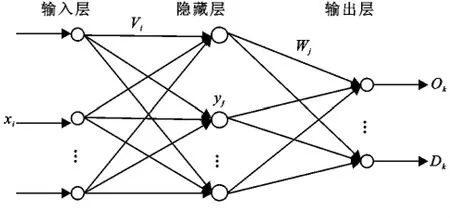
图1 BP网络结构

1.2 BP神经网络的基本原理［4－7］

BP网络将整个学习过程分为两个部分，即网络输入信号正向传播和误差信号反向传播，按照有导师学习方式训练网络。在正向传播中，输入信号从输入层经隐含层逐层计算传向输出层；在输出层，各神经元的输出对应输入模式的网络响应，若输出层得不到期望输出，则误差转入反向传播，遵循减小期望输出与实际输出之间误差的原则，将各单元的误差信息从输出层经中间层回到输入层。层层修正连接权值和阈值，如此循环直至误差信号达到允许范围内或者训练次数达到预先设定的次数为止。节点的作用函数通常选取Sigmoid型函数，简称S型函数，其表达式为：

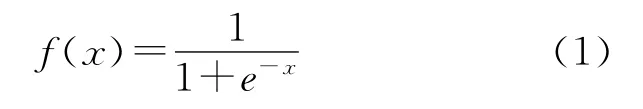
式中：f（x）——为网络节点作用函数；x——为神经元节点的输入值。

标准BP算法的编程步骤为：

（1）数据归一化处理。通过premnmx（）函数对所有样本数据进行归一化处理。

（2）初始化。对权值矩阵W、V 赋随机数，将样本模式计数器p和训练次数计数器q置为1，误差E置0，学习率η设为0－1内的小数，网络训练后达到的精度Emin设为一个正小数。

（3）输入训练样本对，计算各层输出。用当前样本Xp，dp对向量数组X，d赋值，用下式计算隐含层Y和输出层O中的分量。

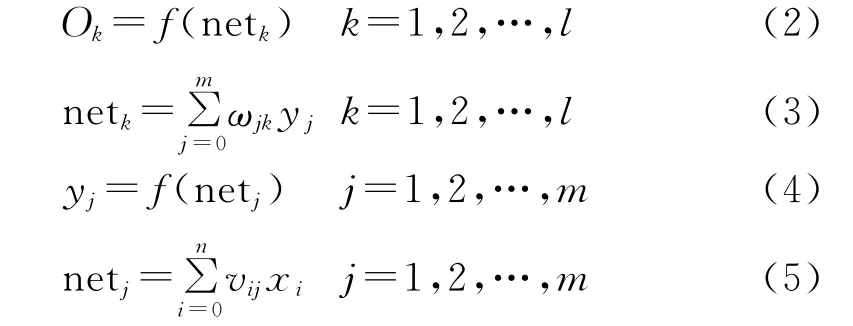
（4）计算网络输出误差。设共有P对训练样本，网络对于不同的样本具有不同的误差Ep，可将全部样本输出误差的平方（Ep）2进行累加再开方，作为总输出误差，也可用诸误差中的最大者Emax代表网络的总输出误差，实际应用中更多采用均方根误差EMRE作为网络的总误差。

（5）计算各层误差信号。应用式（6）计算δok和δyj。

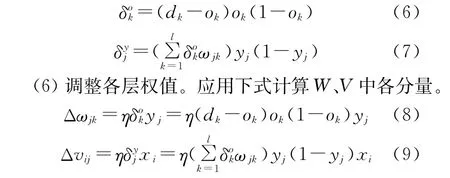
（7）检查是否对所有样本完成一次轮训。若p＜P，计数器p、q增1，返回步骤（3），否则转步骤（8）。

（8）检查网络总误差是否达到精度要求。当用ERME作为网络的总误差时，若ERME＜Emin，训练结束，否则E置0，p置1，返回步骤（3）。

2 实例应用

2.1 原始数据的准备［8－9］

以宝鸡市姜谭堡、十里铺、市区、福临堡、卧龙寺、下马营、石坝河和八里桥8个水源地地下水资料为基础，对各水源地的地下水埋深进行加权平均，概化求得整个研究区范围的平均水位埋深。选取1995—2007年研究区范围内降水入渗补给量、河道渗漏补给量、人工开采量和闸坝蓄水渗漏量作为输入因子，将研究区年均地下水位作为输出因子，建立BP模型进行模拟，然后用训练好的网络预测2008年的地下水位埋深。

2.2 建立模型及预测地下水动态

采用快速BP算法训练网络时，设定显示间隔次数为50，最大循环次数为10 000，目标误差为1×10－3，初始学习速率为0.7，学习速率增加的比率为1.3，学习速率减小的比率为0.8，动量常数为0.9，最大误差比率为0.7。将归一化后的13个学习样本依次输入BP网络，按上述快速BP学习算法的步骤反复训练。在训练了1 028次后，其均方误差MSE＝9.9910E－05，结束网络训练，结果见图2。

图2 BP网络训练结果

模型训练完毕，达到要求误差精度后，用训练好的网络进行仿真，对1993—2007年的地下水位埋深进行模拟，并预测2008年的地下水位埋深，网络输出值为22.4m。此时将2008年水位埋深归入模拟值中，同时绘制网络拟合下的地下水位年际变化图（图3）。由图3可见，宝鸡市地下水位在逐年上升，尤其在1998—2001年和2004—2007年间，曲线变化比较明显，水位上升幅度较大。为了检验模拟的精度，本文选用了灰色模型［10－12］GM（1，n）进行计算，并将其与BP网络相应的模拟结果进行对比，计算出各自的相对误差，结果见表1。

图3 地下水位年际变化

表1 地下水位模拟及预测结果

表1说明，BP神经网络的相对误差介于0.07%～1.98%，比灰色模型（0.13%～6.41%）的精度高。

图4 BP神经网络和灰色模型预测水位埋深对比

由BP神经网络和灰色模型预测的水位埋深对比图（图4）可知，1994—1996年地下水位保持不变，1996—1998年地下水位呈下降趋势，1998—2003年地下水位呈上升趋势，2003—2005地下水位基本保持不变，2005—2008年地下水位呈上升趋势。总体而言，宝鸡市地下水位呈上升趋势，这主要是由于宝鸡市政府实施逐年关停自备井，地下水开采量的大幅度减少使得地下水资源得到了有效的补充与涵养。

3 结论

（1）本文利用宝鸡市8个水源地地下水资料，对各水源地的地下水埋深进行加权平均，概化求得整个研究区范围的平均水位埋深，将研究区范围内降水入渗补给量、河道渗漏补给量、人工开采量和闸坝蓄水渗漏量作为输入因子，将研究区地年均地下水位作为输出因子，建立BP神经网络模型，结果表明，宝鸡市地下水位呈上升趋势。

（2）通过与传统的灰色模型［13］作对比，BP模型和灰色模型的平均相对误差分别为0.55%和3.45%，因而BP神经网络有较高的预测精度，结果真实可靠，对该灌区地下水位监测预报和合理开发利用地下水具有一定的指导意义。

［1］ 平建华，李升，钦丽娟，等.地下水动态预测模型的回顾与展望［J］.水资源保护，2006，22（4）：11－15.

［2］ 赵胜利，刘燕，李书全，等.用BP神经网络预测地下水动态［J］.河北农业大学学报，2002，25（4）：205－207.

［3］ 张忠永，王明涛，贾惠艳.人工神经网络在地下水动态中的应用［J］.辽宁工程技术大学学报，2002，21（4）：504－506.

［4］ 郑书彦，李占斌，李喜安.地下水位动态预测的人工神经网络方法［J］.西北水资源与水工程，2002，13（2）：14－16.

［5］ 赵延涛，姜保良.基于BP神经网络的地下水水位预测［J］.勘察科学技术，2001（4）：7－10.

［6］ 温忠辉，廖资生.用神经网络模型预测济宁市地下水水位变化规律［J］.水文地质工程地质，1995（5）：14－16.

［7］ 陆衍，过仲阳，顾慧娜，等.人工神经网络在地下水评价中的应用简述［J］.上海地质，2001（2）：25－28.

［8］ 徐春迪，郭俊理，宋军林.宝鸡市水资源问题及其可持续利用［J］.水资源与水工程学报，2006，17（5）：77－83.

［9］ Jin Mei－juan，Zhang Jun－hui.Study on the problems of the sustainable utilization of water resources in Baoji City［J］.Journal of Baoji University of Arts and Sciences，2006，26（3）：230－236.

［10］ 孙玉兰，王茂廷.基于灰色模型GM（1，1）的疲劳寿命预测［J］.科学技术与工程，2011，11（3）：560－562.

［11］ 邓丽娟，魏光辉.基于灰色模型的城市用水量预测［J］.地下水，2011，33（1）：100－101.

［12］ 刘洪，孙国曦，曹瑞祥.GM（1，1）动态模型在吴江市地下水水位预测中的应用［J］.地质灾害与环境保护，2008，19（3）：47－51.

［13］ 郝健，刘俊民.GM（1，1）模型改进技术在咸阳市地下水动态预测中的应用［J］.水土保持研究，2011，18（3）：252－254.