应用分形理论计算碳酸盐岩地层胶结指数m值

2012-09-06姜虹范宜仁陈华

测井技术 2012年3期

姜虹，范宜仁，陈华

（1.中国石油大学地球资源与信息学院，山东青岛266555；2.中国石化股份胜利油田分公司地质科学研究院，山东东营257015；3.中国石油大学CNPC测井重点实验室，山东青岛266555；4.中国石油大学理学院，山东青岛266555）

姜虹1，2，范宜仁1，3，陈华3，4

碳酸盐岩储层具有复杂的孔隙空间结构与较强非均质性，致使胶结指数m值出现了规律性异化。引入分形几何理论，以岩心分析数据和测井数据为依据，开展复杂碳酸盐岩储层分形特征及应用技术研究。以岩心数据作为一个时间序列，通过嵌入维数与无标度区的自适应计算方法，在完善关联维数算法的同时，建立了岩心分维值与胶结指数m的基本关系；分析测井曲线的分形特性，以分形理论为桥梁，建立了测井曲线分维值与m值之间的函数关系，实现了通过测井曲线求取m值的设想。

测井曲线；分形理论；关联维数；岩心分析；胶结指数；碳酸盐岩

0 引言

分形［1］几何在石油地质、岩石物性等方面已经得到广泛应用。近期研究表明，大多数岩石的原生、次生孔隙，以及裂缝和溶洞网络，即使其孔隙尺寸变化极大（纳米级至几十米级尺度范围），但均呈现分形结构的特点。这些分形对象的大小、形状、位置以及孔隙度、渗透率等其他属性参数的统计分布，都将遵从储层非均质性指数定律，可用分形几何进行描述，同时这些貌似复杂的现象仅用少量的参数（如分数维）便可以表征［2］。

分形理论在测井中也有一定的应用，分数维与阿尔奇公式的胶结指数m值直接相关，且已有利用测井曲线资料与地层的分形特性求取地层胶结指数m值的先例。鉴于岩心实验数据能够准确且直观反映地层的孔渗特征，可以从岩心数据出发，研究岩石孔隙结构的分形特征。本文分别从岩心数据和测井曲线数据2个角度，利用分形理论建立分数维与胶结指数m值的基本关系。

1 关联维数算法

1.1 G－P算法

关联维数的计算方法有很多种，其中应用比较广泛的是G－P算法。G－P算法基本过程［3］：① 相空间重构：将一个指定的时间或空间数据系列构造成一个d维的相空间［4］（d称为嵌入维数）；② 求出以上向量当中所有点对的距离γij；给出一个数r＞0，将所有点对的距离γij与r相比较，求出小于r的γij数目；③求关联积分函数C（r）：所有小于r的点对距离γij的数目在所有点对数中的比例。

若分形存在，r取充分小值，在某一区间内关联积分函数会逼近式（1）。C（r）＝rD，其中D为关联维数。所以，将关联维数定义为

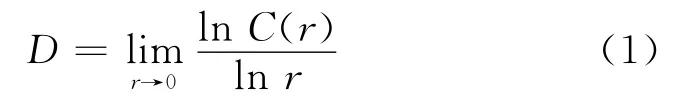
在上述算法过程中，核心问题是嵌入维数d和无标度区的确定。如图1所示，不同的嵌入维数所对应的ln r－ln C（r）的双对数曲线不同，导致关联维数计算不稳定、不准确。而无标度区的确定通常是人工给出，缺乏客观性。有必要研究适合岩心分析数据的嵌入维数d和无标度区的自动计算方法。

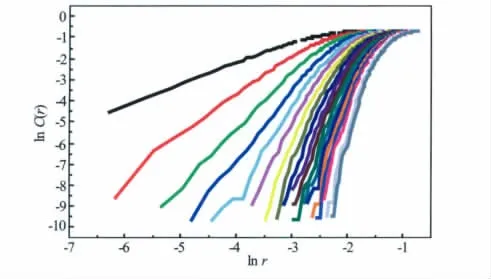
图1 嵌入维数1：20对应的ln r－ln C（r）的双对数曲线图

1.2 嵌入维数d的确定

一般情况下，在给定时间序列进行相空间重构时，其嵌入维数的确定根据Takens定理［5］得到，认为当嵌入维数d≥2D＋1（D为原动力系统吸引子维数）时，重构相空间和原动力学系统的相空间拓扑等价。但这一结论的前提是数据量无限长且无噪声干扰，显然，实际测量的岩心分析数据无法满足以上要求，而且计算的嵌入维数未必是最小嵌入维数，这样容易增加计算的复杂度，影响计算的准确性。因此选择一个合适的嵌入维数，进行有效的相空间重构十分关键。

使用Cao方法确定嵌入维数，定义一个E（d）［6］

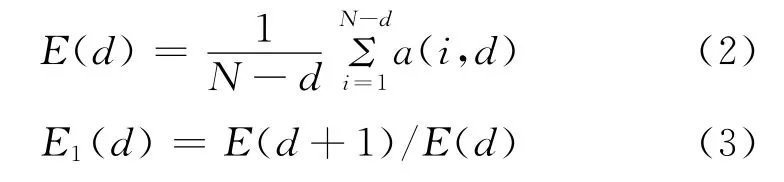
式中，d为嵌入维数；N为数据列长度；a（i，d）＝‖yi（d＋1）－yn（i，d）（d＋1）‖／‖yi（d）－yn（i，d）（d）‖，yi（d）为重构相空间中第i个向量，yi（d＋1）是以d＋1为嵌入维数重构的相空间中的第i个相量，n（i，d）（1≤n（i，d）≤N－d）是一个整数，yn（i，d）（d）是在重构的d维相空间中与yi（d）最邻近的点，如果yn（i，d）（d）＝yi（d），将用第2邻近的点代替它。

随着d不断增大，E1（d）将会趋近于一个稳定值（程序中设定了一个下限值δ，当ΔE1（d）＜δ时就认为E1（d）趋近于一个定值），当E1（d）不随d的增大而变化时，就将此时的d定义为重构相空间的嵌入维数（见图2，嵌入维数d＝10）。图3为确定嵌入维数为10对应的ln r－ln C（r）双对数曲线图。在确定嵌入维数之后，无标度区的确定通常是人工给出的，缺乏客观性，因而有必要研究适合岩心分析数据的无标度区的自动计算方法。

图2 嵌入维数d－E1（d）关系图

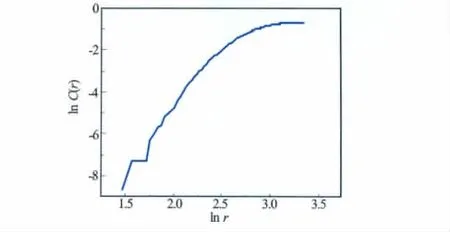
图3 嵌入维数为10的ln r－ln C（r）曲线图

1.3 无标度区的确定

一般研究的分形系统并非严格意义上的自相似，严格的自相似仅存在于一定的尺度变化范围内，一旦超出了这个尺度变化范围，其自相似性就不存在，这个尺度的变化范围就是分形无标度区。根据分形理论的标度不变性，当r在分形的无标度区内变换时，函数C（r）与r之间呈指数关系，即ln r与ln C（r）之间呈线性关系。

①根据G－P算法，得到ln r－ln C（r）的双对数点图，将所有的点拟合成较平滑的n次曲线，并对该曲线上的每个点分别求一阶导数和二阶导数（见图4）。②由于理想的线性区域的二阶导数为0，因此为了寻找到无标度区域，定义了一个门限值ε，将曲线上二阶导数值小于ε的每个区间都找出来。③分别将每个区间中的点进行最小二乘法拟合，并求出拟合度以及拟合后直线的斜率。④ 比较各区间的点拟合成直线后的拟合度，拟合程度最高的区间即为无标度区，该区间直线斜率为关联维数（见图5）。

图4 ln r－ln C（r）拟合曲线及一、二阶导数图

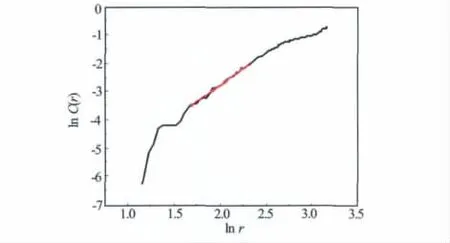
图5 无标度区拟合度99.16%

2 豪斯道夫维数算法

具有分形特征的图形其覆盖尺度与测度之间存在指数关系，测井曲线为采样间隔相等的曲线，定义覆盖曲线的尺度ε与曲线测度μ（k，ε）的关系式为［7－9］

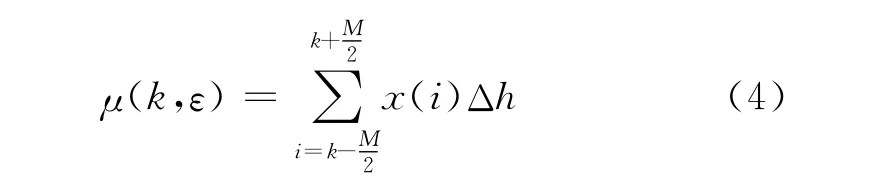
式中，Δh为测井曲线采样点的采样间隔；x（i）为深度i·Δh的测井值；ε＝M·Δh为覆盖测井曲线的尺度；μ（k，ε）为点k处对应尺度ε的测度，当覆盖尺度ε缩小（或扩大）a倍，测度μ（k，ε）将缩小（或扩大）b倍，测井曲线的豪斯道夫维数Df可表示为［10－11］

当豪斯道夫维数Df大于拓扑维数时，可以认为曲线具备分形特征。测井曲线具备分形特征的条件即分形维数Df应在1～2之间变化。

3 相似维数算法

如果一分形集合S可以划分为N个同等大小的子集，每一子集为原集合放大r倍，则集合S的相似维数dS定义为［3］

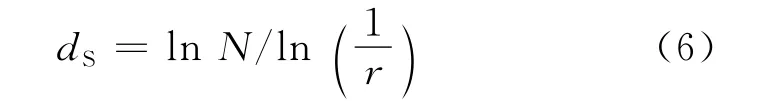
相似维数值范围在一般曲线维数值1和平面维数值2之间。

4 将关联维数算法应用于岩心数据求取胶结指数m值

选取某碳酸盐岩区块的5口井进行研究，以这5口井取心的岩心分析数据为研究对象，以岩心实验测量的孔隙度为原始数据进行处理，依据上述关联维数的计算方法，分别对每一口井取心的孔隙度进行了关联维数的计算分析，结果见表1。

表1 某区块5口井胶结指数m与关联维数D数据表

以此建立的模型方程m＝2.4251－0.2119D，拟合程度为95.0%。将×6井的数据代入建立的模型进行验证，×6井的取心孔隙度的关联维数值为1.396，其胶结指数m值为2.149。将×6井的取心孔隙度的关联维数值为1.396代入模型计算得到的m0＝2.16，误差分析（m－m0）／m≈0.005。在误差允许范围内，在该区块内，上述模型比较适用。

将以上模型与孔隙度－胶结指数的交会图对比（见表2），得出其拟合程度仅为86.3%，对比后可以明显看出胶结指数m与孔隙度φ之间没有明显的线性相关性。将计算得到的孔隙度的关联维数D与胶结指数m交会，能得出两者有一定线性相关性。

表2 某区块5口井的胶结指数与孔隙度数据表

以上是对该区块各井取心的孔隙度数据进行的关联维数计算，得到孔隙度的关联维数与胶结指数m值之间有一定的线性相关性。说明碳酸盐岩地层的孔隙应该具有一定的分形特征，胶结指数m值变化范围大，但仍有规律可循。

5 分形理论应用于测井曲线计算m值

利用计算得到的测井曲线分维数就可以间接反映地层信息，如地层的孔隙结构、非均质性等地层信息都能够比较准确求出。

5.1 测井曲线的分形特征分析

图6至图9分别为声波、电阻率、自然伽马及井径测井曲线的分形特征图。从图6至图9可以看出，声波曲线（Df＝1.03）、电阻率曲线（Df＝1.13）、自然伽马曲线（Df＝1.04）以及井径曲线（Df＝1.01）的豪斯道夫维数都大于其拓扑维数1，而且拟合程度都在97%以上，因此以上测井曲线具备分形特征，可以用来进行分形计算。

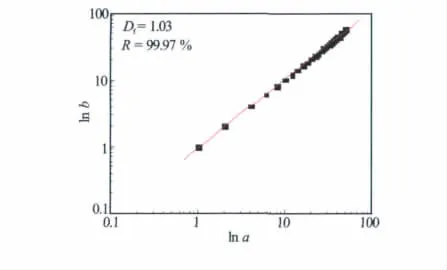
图6 声波测井（AC）曲线分形特征

5.2 相似维数法求m值

在一段储层中，用边长为L1的正方形网格覆盖电阻率测井曲线，边长为L2的正方形网格覆盖声波测井曲线，可以得到2种测井曲线的相似维数d（Rt）和d（lnφ）。用阿尔奇公式进行m值计算时，如果该段储层的流体性质以及岩石的岩性物性变化不大，可以推导得到利用测井曲线分数维计算胶结指数m值（令电阻率测井曲线的覆盖尺度L1与声波测井曲线的覆盖尺度L2都等于L）的表达式［12］

利用上述方法，对某碳酸盐岩区块××2井进行胶结指数m值计算，取××2井4 921.4～5 203.36m井段，按照储层的岩性、物性以及流体性质特征，将该井段分为11个层段，取L为10－4分别对声波测井曲线和深侧向测井曲线进行覆盖，得到lnφ和ln Rt，进而进算出胶结指数m值，并将计算值与岩电实验测量结果进行对比（见表3）。

图7 电阻率测井（Rt）曲线分形特征

图8 自然伽马测井（GR）曲线分形特征

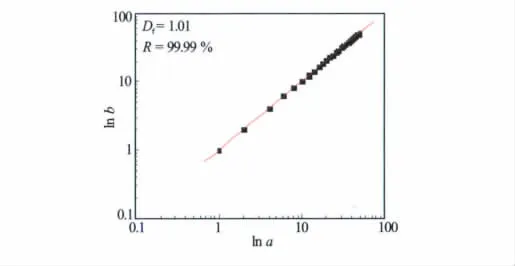
图9 井径测井（CAL）曲线分形特征

将通过分形计算得到的胶结指数m值与取心实验测量结果对比可见，平均误差在8.0%以下，在误差允许范围内，计算结果能够比较准确地反映岩石的孔隙结构特征，因此利用测井曲线分维数求胶结指数m值可行。常规采用岩石物理实验方法求取胶结指数m最直接而且准确，但是取心和岩石物理实验过程复杂而且耗费人力物力，通过测井曲线计算得到m值，是比较有意义的。

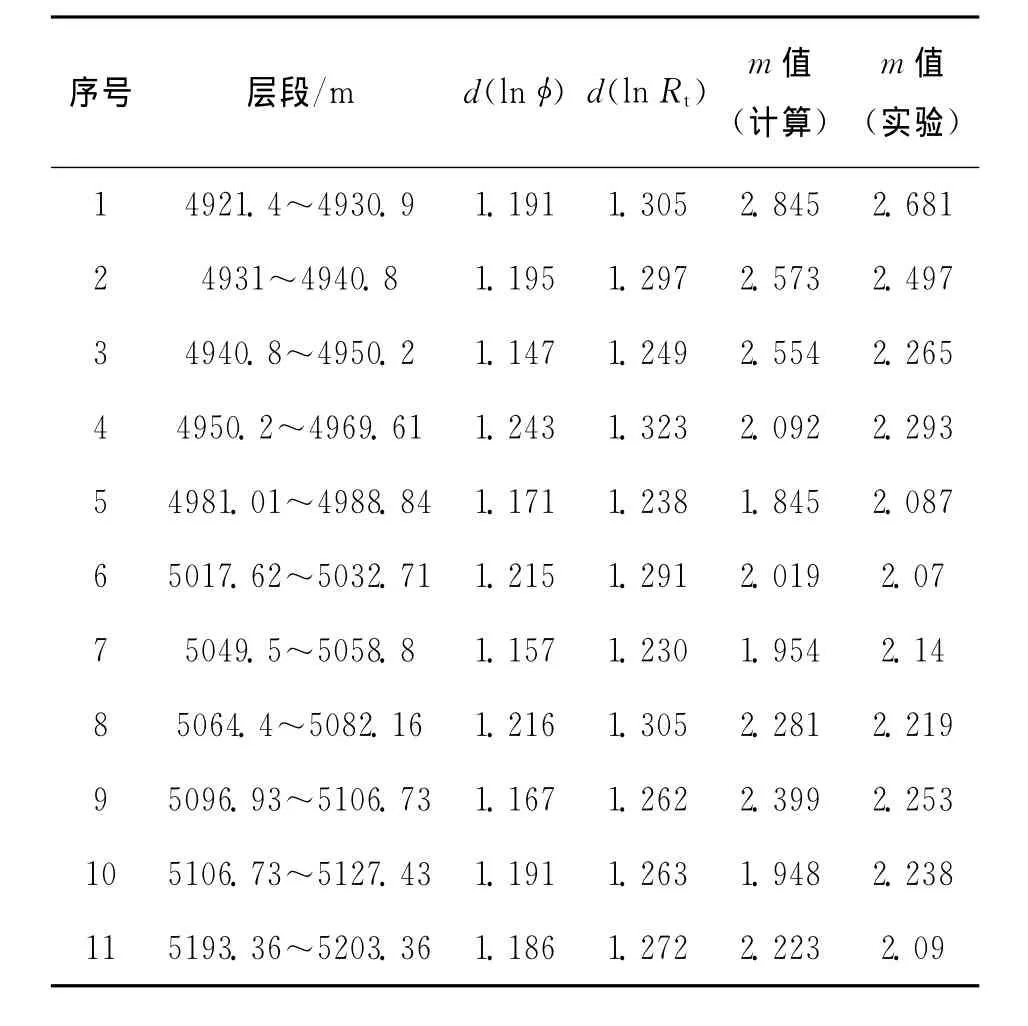
表3 利用测井曲线分维数计算胶结指数m值与实验测量值对比表

5.3 关联维数法求m值

测井曲线采样点也是一个时间序列，将关联维数应用于测井曲线求取m值方法同样适用。为建立岩心m值与测井曲线关联维数值的一一对应关系，需将岩心归位后，求取归位深度处各相关测井曲线的关联维数值。将每个测井数据序列求出的关联维数值，作为该数据列中点数据深度处的分维值，基本能够反映该深度处的测井曲线分维特征，并且做到了分维值与深度的一一对应。

常规测井曲线当中，与孔隙结构指数m值密切相关的主要是三孔隙度曲线（声波、中子和密度），其分形维数可表示为dAC、dCNL、dDEN，由叠加和匹配原理可以得到一个与地层孔隙结构相关的分形维数值dm

［13］［见式（8）］，dm综合反映了地层信息，与胶结指数m之间应该有相关性。

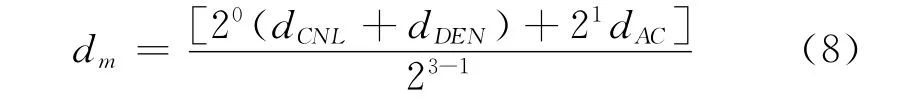
将岩心归位后，首先计算归位深度处的dm值，将dm值与岩心分析得到的胶结指数m之间进行比较（见表4），分别取某碳酸盐岩区块某组上、下段岩心与测井曲线分维值进行对比分析，发现dm与m之间具有较好的线性关系，见图10与图11，拟合关系式见式（9）和式（10）。

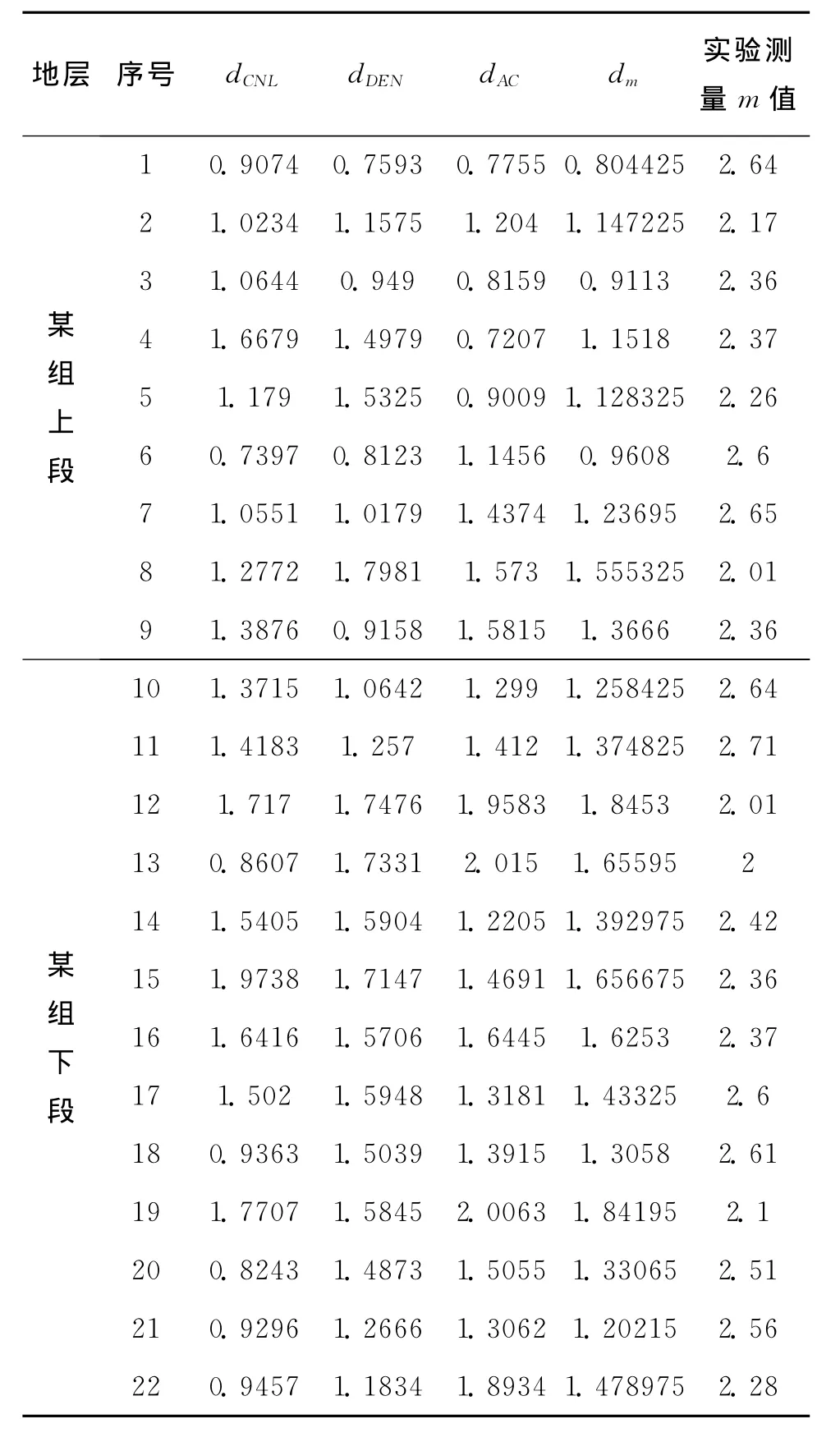
表4 利用测井曲线关联维数求取胶结指数m值

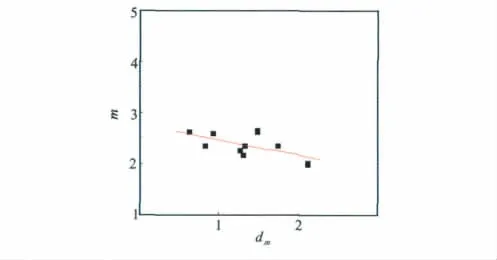
图10 某组上段m与dm关系图

某组上段m与dm的关系式

某组下段m与dm的关系式

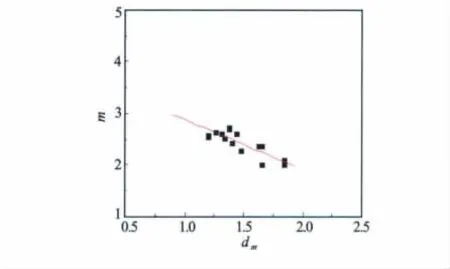
图11 某组下段m与dm关系图

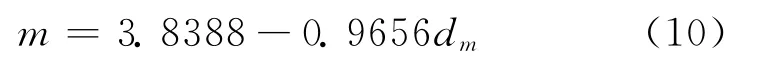
式（9）、式（10）的分形几何规律与储层的地质特征是相符的。分维数本身反映的是样本空间的变化剧烈程度，dm综合反映三孔隙度曲线的变化剧烈程度，dm越大则地层结构越复杂，即dm与地层的非均质性成正比。储层级别越高，其孔隙的连通性越好，非均质性相对较弱，dm越小；反之，则dm越大。通过对某碳酸盐岩区块岩心实验分析得到，高级别储层的m值较大（原因是高级别储层主要以孔洞型为主），因此dm与m值理论上应该成反比关系，与推导的关系式相符。为验证关系式的正确性，由式（9）、式（10）分别对×6井的3个类储层进行分形计算，得到各类储层的m值与岩心实验分析得到的m值较相符，具体见表5。

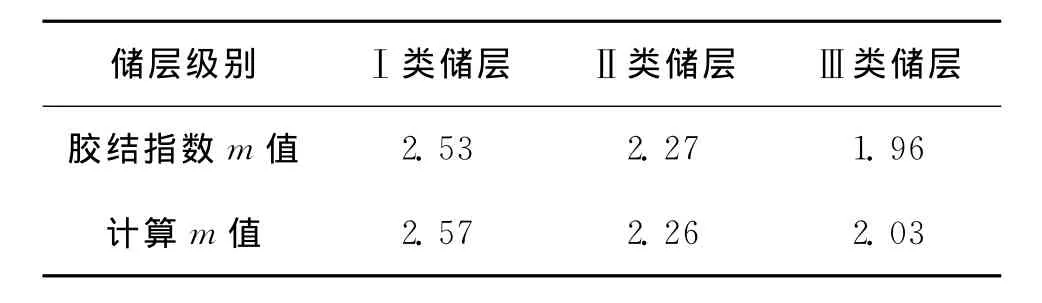
表5 岩心胶结指数m值按储层分类统计表

胶结指数m值与测井曲线的分维值建立良好的线性关系，尤其针对强非均质性的碳酸盐岩储层，m值变化大，且变化规律不易把握，通过引入分形数学的方法，降低了m值求取难度，同时证明复杂的碳酸盐岩储层孔隙结构遵循非均质性指数定律，可用分形几何进行描述。

6 结论

（1）实现了关联维数的自动求取方法，尤其解决了适合对岩心分析数据进行分维数计算的嵌入维数以及无标度区的自动计算方法。

（2）将岩心分析孔隙度数据转化为时间序列，进行了关联维数的计算，得到孔隙度的分维数与胶结指数m值之间有一定的线性相关性，说明碳酸盐岩储层的孔隙应该具有一定的分形特征。

（3）证明测井曲线具有分形特征，并以测井曲线的分维数为桥梁，建立了测井曲线与m值之间的函数关系，实现了通过测井曲线求取m值的设想。

［1］ Mandelbrot B B.The Fractal Geometry of Nature［M］.New York：W.H.Freeman And Company，1982.

［2］牟书令.中国海相油气勘探理论技术与实践［M］.北京：地质出版社，2009.

［3］王域辉，廖淑华.分形与石油［M］.北京：石油工业出版社，1994.

［4］陈颙.分形与混沌在地球科学中的应用［M］.北京：学术期刊出版社，1989.

［5］ Takens M.Detecting Strange Attractors in Fluid Turbulence［C］∥Dynamical Systems and Turbulence，Lecture Notes in Mathematics.Berlin：Springer.1986.

［6］ Liangyue Cao.Practical Method for Determining the Minimum Embedding Dimension of a Scalar Time Series［J］.Physica D，1997，110：43－50.

［7］ Pape H，Clause C，Iffland J.Variation of Permeability with Porosity in Sandstone Diagenesis Interpreted with a Fractal Pore Space Model［J］.Pure and Applied Geophysics，2000，157：603－619.

［8］ Cheng Q M.Multifractal Interpolation［C］∥Lippard S J，Nass A，Sinding L.5th Annual Conference［LAMG99］Proceedings：International Association of Mathematical Geology.Norway：Trondheim.1999，245－250.

［9］李庆谋，成秋明.测井曲线分形校正［J］.中国地质大学学报：地球科学，2002，27（1）：63.

［10］谢季坚，邓小炎.现代数学方法选讲［M］.北京：高等教育出版社，2001.

［11］梁齐瑞，赵世龙，丁忙生.自然伽马测井曲线的分形特征分析［J］.物探与化探，2006，30（3）：240－243.

［12］刘红岐，夏宏泉，王拥军，等.地层胶结指数m的分形特征研究［J］.测井技术，2001，25（1）：24－27.

［13］王天波，董春旭，徐丽萍，等.用分形理论确定m、n值的方法及其应用［J］.测井技术，1998，22（1）：16－19.

On Calculation of Cementation Index min Carbonate Formation Using Fractal Theory

JIANG Hong1，2，FAN Yiren1，3，CHEN Hua3，4
（1.College of Geo－resource and Information，China University of Petroleum，Qingdao，Shandong 266555，China；2.Geoscience Research Institute，Shengli Oilfield CO.，SINOPEC，Dongying，Shandong 257015，China；3.CNPC Key Well Logging Laboratory，China University of Petroleum，Qingdao，Shandong 266555，China；4.College of Science，China University of Petroleum.Qingdao，Shandong 266555，China）

Carbonate reservoir with complex pore structure and strong heterogeneity often results in irregular change of the cementation index m.So，fractal geometry theory is introduced.Based on core analysis and log data，carried out are the researches on fractal characteristics and application technology in complex carbonate reservoirs.The core data are transformed into time series，and by using adaptive method of embedding dimension and scale－free zone，the correlation dimension algorithm is modified and meanwhile the basic relationship between fractal dimension of core and the cementation index mis established.Then analyzed are the fractal characteristics of logging curves and built is a function of the fractal dimension of logging curves and mthrough the fractal theory，and therefore figuring out the value mwith logging curves.

logging curve，fractal theory，correlation dimension，core analysis，cementation index，carbonate

P631.84；TE19

2012－01－05 本文编辑余迎）

1004－1338（2012）03－0250－06

姜虹，女，1984年生，硕士，研究方向为测井理论、方法与技术。