一种基于椭圆曲线的Schnorr型多重数字签名
2012-09-06张秉儒
周 敏,张秉儒
(青海师范大学数学系,青海西宁 810008)
1 引言
数字签名在密码学中就是用私有密钥进行加密,接受方用公开密钥进行解密.数字签名技术首先最早是应用于用户登录过程,其次相关的数字证书应用在网上报关,网上采购,电子商务交易,现在还广泛应用于电子邮件,数据交换,电子交易[1].1983年Boyd提出多重数字签名[2]的概念以来,多重数字签名发展的很快,对于不同的数学难题的多重数字签名应运而生.多重数字签名即多个用户对同一消息进行的数字签名,从而实现多个用户对同一消息进行签名方案.根据签名的顺序不同分为有序多重数字签名和广播多重数字签名.有序多重签名是所有签名者按照一定的次序进行签名,每一位签名者在收到前一位签名者签名先对其验证,若验证没通过,则拒绝后面的工作并终止整个签名,若验证通过,则进行接下来的签名.广播多重签名是指在签名过程中签名组成人员之间没有先后顺序,但在每个签名成员签完名后有一个签名收集者来最终完成这个签名.基于椭圆曲线的多重签名是指在椭圆曲线的离散对数问题下的多重数字签名,它比一般基于离散对数问题更加困难.2006年阎希光提出了一种基于椭圆曲线的多重签名[2],2007年李斌等又提出另一种基于椭圆曲线的多重数字签名[3],在同一年他们又提出Schnorr型多重签名[4],而本文基于前人基础上提出了基于椭圆曲线的Schnorr型多重签名它不仅提高安全性,还利用Schnorr签名的特点即密文短,运算速度快.
2 Schnorr型广播多重数字签名
2.1 方案描述
此方案包括系统参数的选取,签名过程和验证过程,方案的参与者即消息发送者U1,若干签名者Ui(i=1,2…n),签名收集者Uc和签名验证者Uv.
2.2 系统参数的选取
选取大素数p,q满足q整除p-1,q和p是整数,g∈Z*p且满足gq=1modp,g≠1,h为单向哈希函数,选取的私钥为x,1<x<q,公钥为y,y=gxmodp,(p,q,g,y,h) 公开.
2.3 签名过程
Step1:每一位签名者Ui(i=1,2…n)任意选取xi∈Z*q,作为Ui的私钥,并计算ri=gkimodp,将其发送给其他签名者Uj(j≠i).
Step2:Uj收到ri后计算R=rimodp和e=h(R,m),然后再计算si=ki-xi(e+R)modq.
Step3:将签名(m,(si,ri))作为用户对m的签名发送到Uc.
Step4:Uc收到(m,(si,ri)) 后,其中i=1,2…,n,按照R=rimodp计算R和e,然后验证方程g-siri=gki=y(e+r)modp
Step5:Uc计算s=s1+s2+…+sn,则多重签名是(m,(s,R)).
2.4 验证过程
消息接收者Uv收到消息(m,(s,R))后,验证(y1y2…yn)(e+R)=Rg-smodp是否成立,若成立则签名有效,否则拒绝签名.

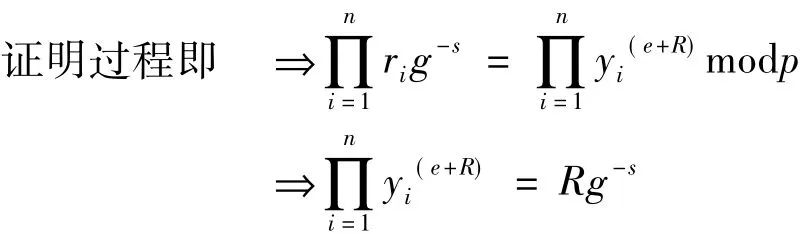
3 基于椭圆曲线的Schnorr型广播多重签名
3.1 参数选取
设N是元素个数为q的有限域,全局参数表示为(q,FR,a,b,G,n,l),FR为GF(q) 中的一个元素,定义椭圆曲线E:y2=x3+ax+b,基点y2=x3+ax+b,xG,yG∈GF(q),G∈E,G的阶为素数n,n>2160,n>4,#E(GF(q))为椭圆曲线构成群的阶,l=#E(GF(q))/n.每一个签名者Ui的私钥为di,相应的公钥为Q=diG∈E(GF(q)),Ui的公钥为Qi=diG.
3.2 签名生成
UI将m发送到每一个签名者Ui(i=1,2…,n),Ui和Uc收到消息后进行如下操作:
Step1:Ui选择一个随机数ki,ki∈[1,n-1]计算kiG=(xi,yi),ri=ximodn,Ui将ri发送给签名收集者Uc
Step2:Uc收到ri后,计算R1=rimodp和e=h(m,R1)将R1发送每一位签名者Ui(即将R1广播出去).
Step3:对消息m,Ui计算si=ki-di(e+R1)modn,si作为用户Ui对消息m的签名,将(si,ri)发送到Uc.
Step4:Uc收到(si,ri) 后,计算R1=rimodp,s=s1+s2+…+…sn,然后将(si,ri,R1) 发送签名收集者Uv.
3.3 验证过程
Uv收到签名后(si,ri,R1) 后,计算Xi=siG-(e+R1)Qi=(xi,y1),验证vi=rimodn是否成立,其中(i=1,2…n),如果等式成立则认为Ui对消息的签名有效,否则签名无效.


由上述推论过程可得,Uv收到签名(s,ri,R1)后验证vi=rimodn是否成立,才能确定所有签名是否有效.
4 安全性分析
4.1 体制上的安全
首先,基于椭圆曲线体制上,且定义在GF(q)上,G是椭圆曲线上有理子群,设A,B满足B=kA,k∈[0,n],求出k是困难的,这是基于椭圆曲线的离散对数问题,因此该方案基于椭圆曲线上就保证了其安全性.其次,Schnorr型的密文比ELGamal型的密文短,所以该签名比基于椭圆曲线ELGamal型多重数字签名运算速度快.
4.2 防完全攻破
它所依赖的主要是哈希函数,该签名在签名生成过程中引进了哈希函数e=h(),伪造者伪造e',从而计算m是困难的,因为哈希函数伪造者无法计算.
4.3 防一般伪造
对于每个签名者Ui签名si=ki-di(e+R1)modn,其验证方程为:vi=rimodn和对于收到签名消息(si,ri)的签名收集者Uc,有式子R1=rimodp和si=s1+s2+…+sn所得出的消息签名(xi,ri,R1),若攻击者欲以Uc的身份伪造所有签名Ui的签名即求解(si,ri,R1) 满足Xi=siG-(e+R1)Qi=(xi,yi),得vi=rimodn它是困难的.
5 结束语
本文首先给出了一种Schnorr型的多重数字签名方案,并由前人的理论依据给出了一种基于椭圆曲线的Schnorr型的多重数字签名方案,并对其进行验证,此外还对其的安全性进行了分析.
:
[1]赵泽茂.数字签名理论[M].北京:科学出版社,2007:67-68.
[2]阎希光.基于椭圆曲线的多重签名[J].网络安全技术与应用,2006,35(3).
[3]李斌,赵泽茂,李继国.基于椭圆曲线的多重数字签名方案[J].计算及应用与软件,2007,24(4).
[4]李斌,赵泽茂,龚少麟.Schnorr型多重数字签名方案[J].河海大学常州分校学报,2005,19(3).
