基于GRNN的主要编组站办理车辆数的预测

李益民

（中国铁道科学研究院 运输及经济研究所，北京 100081）

基于GRNN的主要编组站办理车辆数的预测

李益民

（中国铁道科学研究院 运输及经济研究所，北京 100081）

运用广义回归神经网络对铁路编组站办理车辆数进行预测。在对编组站办理车辆数的经济因素和结构因素进行分析的基础上，给出GRNN预测的全过程，并将GRNN与BP网络预测进行比较，建立网络、训练和检测，最终模拟得到全路主要编组站办理车辆数。实例分析证明GRNN能提高预测精度，为编组站规划和设计提供理论支持。

铁路；编组站；办理车辆数；有调中转车；无调中转车；广义回归神经网络

1 概述

编组站在铁路路网运输中承担大量的列车改编作业，编组站办理车辆数的效率直接关系到路网运输效率和运输质量。编组站办理车辆数是衡量和评价编组站运营效果的重要指标，编组站的发展规划需要对未来年办理车辆数进行预测。另外，该类指标对于评估车站作业的负荷和车站作业能力的适应性，以及确定编组站改编设备配置，都具有十分重要的作用。

编组站办理车辆数不仅受到铁路内部因素的影响，也会随着国民经济的发展发生变化，而选择相关的重要影响因子将有助于提高预测结果的可靠性。另外，短期预测会减小预测的相对误差，使得预测结果更具有实际意义。

以铁路40个主要编组站总办理车辆数、有调中转车和无调中转车为研究对象，选择若干宏观经济指标作为重要的影响因子，运用广义回归神经网络（Generalized Regression Neural Network，GRNN）进行5年的短期预测。

2 广义回归神经网络的基本结构

目前，常用的预测方法有时间序列法（移动平滑法、指数平滑法和季节调整法）、相关（回归）分析法、灰色预测法和多种方法综合的组合预测方法等。这些方法大都集中在对其因果关系回归模型和时间序列模型的分析上，因而所建立的模型适用范围有限。

人工神经网络作为一种并行的计算模型，具有传统建模方法所不具备的很多优点，有很好的非线性映射能力，一般不必事先知道有关建模对象的结构、参数和动态特性等方面的知识，只需给出对象的输入、输出数据，通过网络本身的学习功能就可以得到输入输出的映射关系。

办理车辆数的预测可以利用BP（Back Propagation）网络模型和径向基函数（Radial Basis Function，RBF）网络模型，但是这两种模型在用于预测时，存在收敛速度慢和局部极小的缺点，在解决样本量少并且噪音较多的问题时，效果并不理想。

广义回归神经网络在逼近能力、分类能力和学习速率上较BP网络和RBF网络有较强的优势，模型最后收敛于样本集聚较多的优化回归面，并且在样本数据较少时预测效果也比较好。此外，网络模型还可以处理不稳定的数据。因此，采用GRNN建立网络预测模型，对办理车辆数进行预测。

GRNN网络的基本思想是，用径向基函数作为隐单元的“基”，构成隐含层空间。隐含层对输入向量进行变换，将低维空间的模式变换到高维空间内，使得低维空间内的线性不可分问题在高维空间内线性可分，广义回归神经网络结构图如图1所示。图1中，X=x1，x2，…，xn，为网络输入向量；ϕj（X）（j=1，2，…，m）为任一隐节点的激活函数，W为输出权矩阵，T为输出层阀值向量；Y=y1，y2，…，yl，为网络输出向量[1]。

3 全路主要编组站办理车辆数的预测

3.1 影响因素分析

通过调查分析，影响主要编组站办理车辆数、有调中转货车数和无调中转货车数的因素包括经济因素和结构因素两部分，如表1所示。

图1 广义回归神经网络结构图

表1 编组站办理车辆数影响因素分析表

经济因素和结构因素涵盖了宏观与微观的相关因素，宏观上，GDP、工业总产值、CPI、进出口总额、社会消费品零售总额和人口作为大的指标，对于国家货物的流动有重要影响；微观上，横向市场竞争的公路货运量，纵向的铁路内部指标包括全国铁路营业里程、货车日均装车数、机车（货车）的拥有量和铁路货运量，将直接影响办理车辆数。煤炭、钢铁和粮食属于最主要大宗货物，主要采用无改编运输形式，直接影响无调中转车数。

3.2 数据样本

选择以上15个因素作为影响因子，主要编组站办理车数、有调中转车数、无调中转车数作为输出因子，构建GRNN。

以2001—2009年数据作为网络的训练样本，以2010年样本作为外推预测检验，如表2和表3所示，预测目标样本如表4所示。

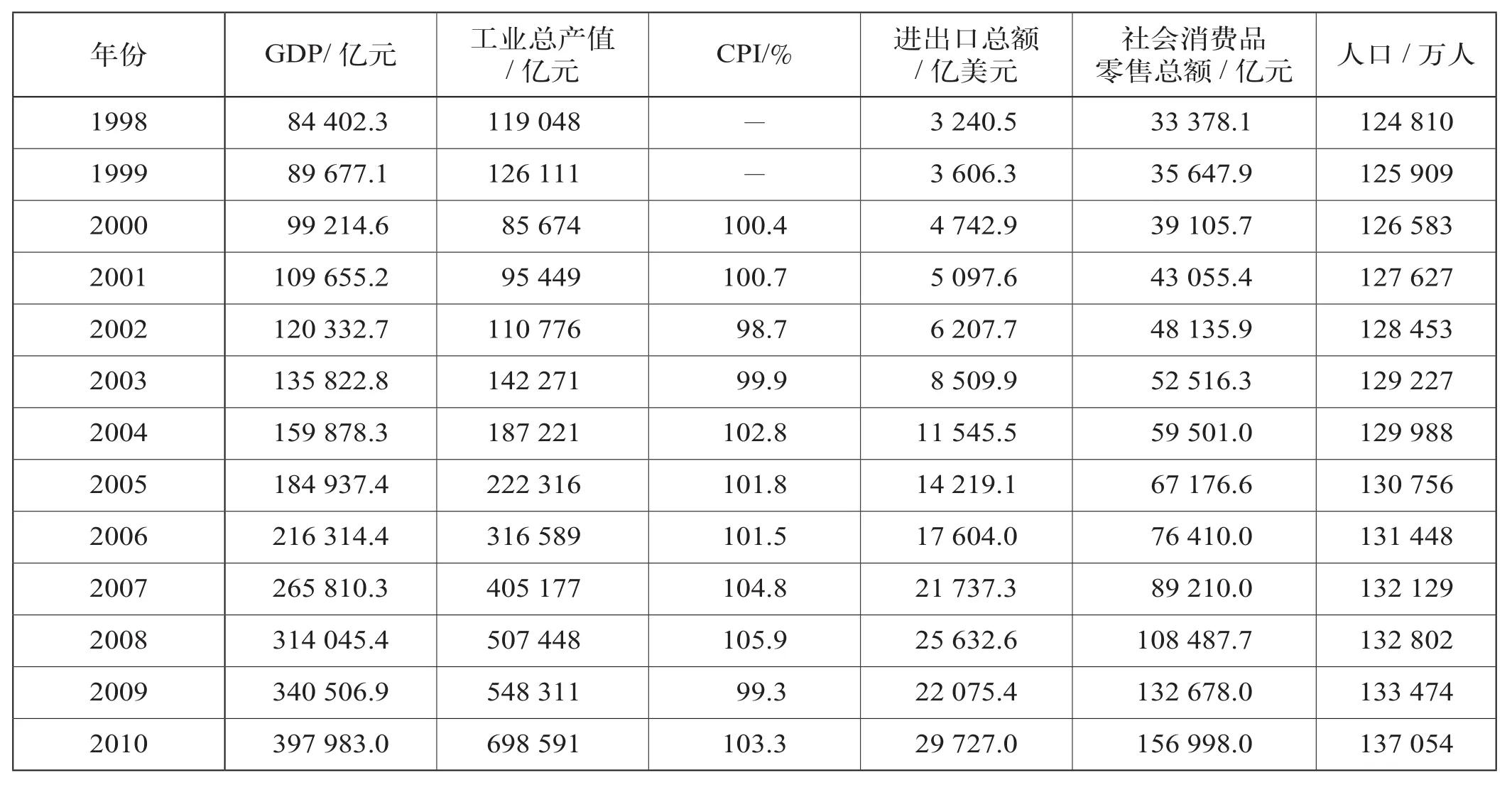
表2 样本数据表1

表3 样本数据表2

3.3 预测模型的建立

3.3.1 训练和预测1

为了得到短期内2011—2015年全路主要编组站办理车辆数、有调和无调中转货车数，必须得到并补全2011—2015年15个影响因子的基础数据，下面将针对不同的预测因子采用不同的预测方法以期达到最佳效果。

（1）GDP的预测。对于GDP基础数据的预测，不论是单线预测还是非线性的神经网络预测，都可以从原始数据和相隔时间序列差值进行预测，下面将从原始数据和其差值作为历史数据分别做预测，结果如表5所示。

从表5可以看出，以相隔时间序列差值为基础数据作出的预测效果要优于原始数据作出的预测，并且BP神经网络的预测相对误差值达到了0.44%，是比较理想的外推测试效果，下面将通过BP神经网络得到外推数据，如表6所示。GDP的平均增长率为5.3%，这与《十二五规划纲要（草案）》中提出的未来5年目标GDP增长率控制在7%以内相一致。

（2）其他影响因子的预测工业总产值、CPI、进出口总额等其余14个影响因子测试样本预测表如表7所示。测试样本年份为2010年。在对影响因子的预测中，除CPI采用指数平滑预测方法，社会消费品零售总额和国家铁路营业里程采用回归分析预测方法外，其余因子均采用BP神经网络预测方法。

由表5和表7可得到影响因子预测误差平均值为2.18%。

对于影响因子的预测结果如表8和表9所示。

3.3.2 训练和预测2

对样本数据进行归一化处理，以归一化后的样本数据创建一个GRNN网络和BP网络，以计算第t年的主要编组站办理车辆数。

将光滑因子分别设置为0.01，按照0.01步长递增至2寻找最优光滑因子值，通过训练，检查网络对样本的逼近性能。

当光滑因子（步长）spread = 0.67时，均方误差mse取得最小值为0.052 342。即此时网络逼近性能和预测性能的误差都为最小。因此，将光滑因子设定为0.67。

表5 GDP测试样本预测

表6 GDP预测数据

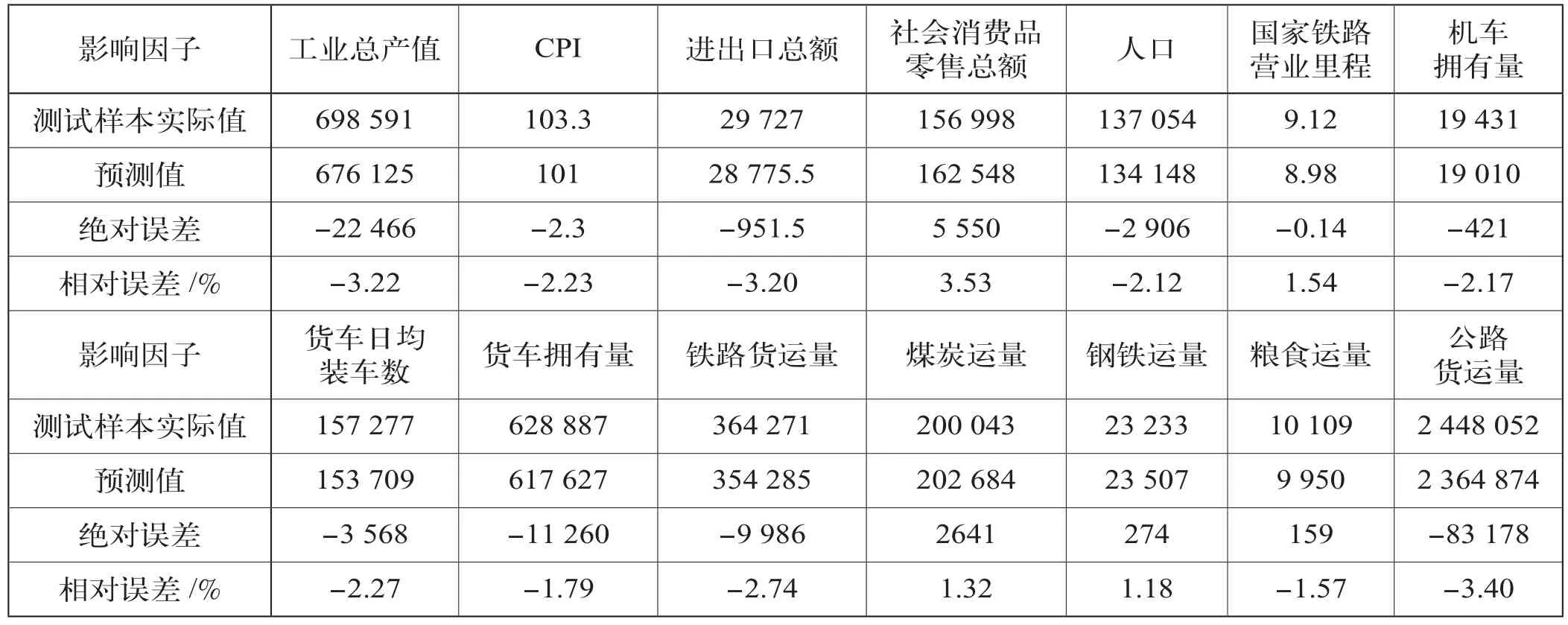
表7 其他影响因子测试样本预测

表8 影响因子预测值1

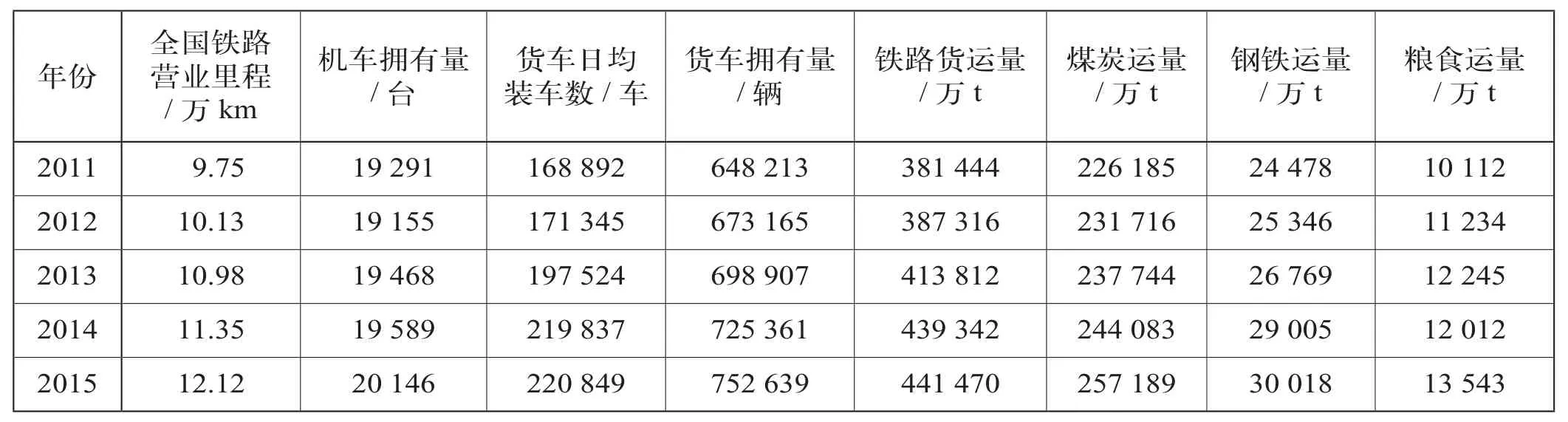
表9 影响因子预测值2

将2010年作为测试预测年，用GRNN网络和BP网络预测总办理车数、有调中转车数、无调中转车数，结果如表10所示。

由表10可以看出，GRNN网络相对于BP在预测精度上更接近实际值，尤其是无调中转车的办理车辆数。考虑2009、2010年数据波幅较大，训练样本容量较小，精度虽然不是十分精确，但是预测结果还是可以接受的。

运用训练完毕的网络，将表8和表9中的影响因素值作为输入向量，对2011—2015年的编组站办理车辆数、有调和无调中转货车数进行预测，其结果如表11所示。

表10 网络 1 预测结果

表11 网络 2 预测结果

根据调研得知，无调中转车数在地方性、区域性和路网性编组站上升趋势相对明显，有调中转车数比较平稳，总办理车辆数依然稳中有升，这和预测数据的趋势较一致。

4 结束语

基于分析全路编组站办理车辆数的影响因素及特点，经过预测效果的检验和分析，证明了利用GRNN神经网络进行预测的有效性。

实例分析表明，GRNN在设定的条件下，输入和输出结果关系明显，模拟结果稳定，预测结果与接近年份的数据相关度更大；在直接影响因素缺失的情况下，能够反映出数据时序的变化规律；GRNN神经网络虽然在趋势修正上优于其他时间序列法，但有突发的干扰波动影响时，此时若没有与干扰存在关联的参数作为影响因子进行广义回归神经网络预测的输入向量，外推预测数据也会存在较大误差。

：

[1] 张德丰. MATLAB神经网络应用设计[M]. 北京：机械工业出版社，2009.

1003-1421(2012)02-0051-06

TP183；U291.4

B

2011-11-17

2011-12-26

金 颖