用一般脉宽调制器构造的变频式脉宽调制器
2012-09-05孙定浩赵长春
孙定浩,赵长春
(1.北京控制工程研究所,北京100190;2.北京圣业科技发展有限公司,北京100190)
用一般脉宽调制器构造的变频式脉宽调制器
孙定浩1,赵长春2
(1.北京控制工程研究所,北京100190;2.北京圣业科技发展有限公司,北京100190)
提出为直流变换器增加一个控制变量的概念,以弥补现行直流变换器只有一个调节变量引起的一些缺陷.本文选定的控制变量是直流变换器的运行频率f,将它与一次电源电压V联系起来,使f随V上升按预设的规律下降,以解决直流变换器以固定频率运行时这种情况下出现的许多问题,如开关管发热加剧等.实现这一设想的主要问题是将一般脉宽调制器构造成变频式脉宽调制器.现以脉宽调制器1842/3/4/5(简记为184X)和1842A/3A/4A/5A(简记为184XA)为例,给出了将它构造成变频式脉宽调制器的方法,示出了可实现的变频特性.设计了两个将一次电源电压转换为变频式脉宽调制器输入电压的线性转换电路,推导了计算这些电路中各元件参数的表达式.实验结果与设计一致.
变频式脉宽调制器;电压线性转换电路
目前用一般脉宽调制器实现的直流变换器,只有一个调节变量,即以固定频率f产生的脉冲宽度w,没有其他调节变量或控制变量.但直流变换器的外部变量却有多个,如输入电压 V,航天器一次电源电压的变化率约 ±25%;输出功率的变化率更高.用一个调节变量调节直流变换器以适应多个外部变量的变化,使输出电压Vo稳定,虽在技术上可行,但从直流变换器运行的总体结果(除Vo的各项指标外,尚应包括开关管功耗,整机效率,对外辐射等)来衡量,普遍存在许多缺陷.例如 V上升时,在相同输出功率条件下,不论采用何种变换器拓扑,主开关(MOS管)的功耗均上升,发热加剧等.
笔者的思路是,为直流变换器增设一个控制变量,以便为设计者解决面临的缺陷提供一个可能的解决办法.本文选择的控制变量是直流变换器的运行频率f,将它构造成输入电压 V的函数,故用f(V)表示.这函数的特性可由设计者给定,例如将f(V)设置成V的单调下降函数.这样可使各种变换器在 V上升时主开关管的功耗不致上升;对于反激变换器,可使V上升时脉宽不致过窄等.为实现上述思路,首先要解决的问题是如何将一般脉宽调制器构造成与一次电源电压V有关的变频式脉宽调制器,以实现预定f(V)特性.现以航天器中常用的脉宽调制器 1842/3/4/5(简记为184X)和1842A/3A/4A/5A(简记为184XA)为例,讨论这一问题.
文献[1]给出了这类脉宽调制器运行频率 f的一般解析表达式(生产厂给出的数据见文献[2]).现将其中串联RT(定时电阻)和CT(定时电容)的电源电压E作为变量,RT作为参数,故将f记为f(E,RT).令E在4V至6V之间变化,RT分别为1kΩ,1.2kΩ,…,10kΩ,绘制了表征f(E,RT)变化特征的曲线族F(E,RT).其结果表明,以E为变量,RT为参量,这类脉宽调制器可输出我们需要的变频特性.
接着,本文设计了一个以放大器为基础的V/E转换电路,将一次电源电压V转换为电压E,并给出了计算转换电路中各电阻值的公式.这样,便在原理上解决了构造变频式脉宽调制器的问题.
最后,利用本文的解析结果设计了两个变频式脉宽调制器,实验结果与设计预期一致.
1 一类振荡器的变频特性
图1示出脉宽调制器184X和184XA中振荡器的电路模型.按文献[1]的解析结果,其振荡频率f(E,RT)和占比空D(E,RT)的表达式为

图1 振荡器电路模型及等效电路Fig.1 Circuitmodel and effective circuit of oscillation

其中各常数的标称值为VL=1V,VH=2.7V;184X的i=0.013A,184XA的i=0.0083A(各物理量均用国际标准单位).由于CT是一个可由设计者给定的量,RT是参数,故可将式(1)改写成

其中

用函数F(E,RT)表征图1振荡器运行频率与E和RT的关系.表1(a)和(b)分别示出F(E,RT)的计算结果,E在4~6V之间,RT在1kΩ至10kΩ之间.在以上参数范围内,由式(2)计算可知D>0.5.表1中比值F(6,RT)/F(4,RT)表示RT在所示值且E在4~6V之间变化时,Fmax与Fmin的比值.

表1 (a) 184X的F(E,RT)值Tab.1(a) F(E,RT)values of 184X
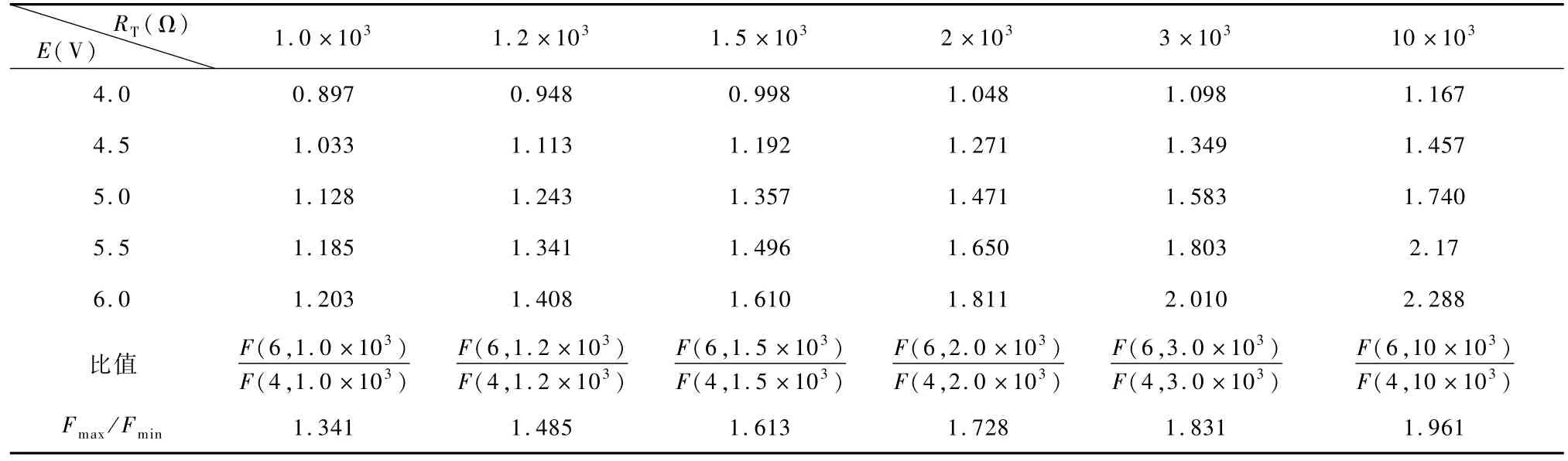
表1 (b) 184XA的F(E,RT)值Tab.1(b) F(E,RT)values of 184XA
按表1(a)和(b)的数据,图2(a)和(b)分别示出184X和184XA的F(E,RT)的曲线族.由图可见,选择不同的RT值,在相同的E的变化范围内可得出不同的F(E,RT)变化规律.设计者可根据期望的运行频率f与电压E的关系,从这曲线族中选定一曲线(例如 RT=2kΩ),并在其右方选定一点p1(E1,2×103)作为最高频率fmax点(参看图2(b)所示).设预定最小运行频率为fmin,其相应的E值用E2表示.由式(3)知,

在RT=2×103曲线上找到F值等于上式值的p2点,其横坐标即E2值.至此,确定了E值的变化范围应在E2至E1.
2 设计V/E转换电路
直流变换器一次电源电压 V在 V1至 V2间变化,V2>V1,要求相应的运行频率在fmax至fmin之间变化.由上述已知,相应的E值应在E1至E2之间变化.因此,变量V和变量E之间应构成图3(a)中由曲线段p1p2所示的关系.

图3 V/E转换电路情况Fig.3 Situation of V/E transformation circuit
将直线段p1p2延长至与V轴、E轴相交,得直线p0p1p2p3.此直线方程为

其中:

令式(6)中E=0,得
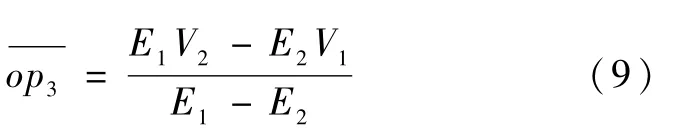
现用电路分析法讨论图3(b)电路实现的V/E线性转换.当V=0时,A1点与A2点电位为零.流经R3的电流为Vref/R3,向左流动.因R3和R4流过相同的电流,故输出的电位为

当输出端电位为零时,流经R4的电流为Vref/R4,向右流动.因R3、R4流过相同的电流,故此时A2的电位为

另一方面,A1的电位为

因VA1等于VA2,故由式(11)和(12)得

令图3(a)和(c)中相应的截距相等,可得

由式(14)和(15)得

式(17)和(18)给出图3(b)电路中各电阻应满足的条件.
现用电路分析法讨论图3(d).当V=0,R1与R2并联,流经R3的电流为
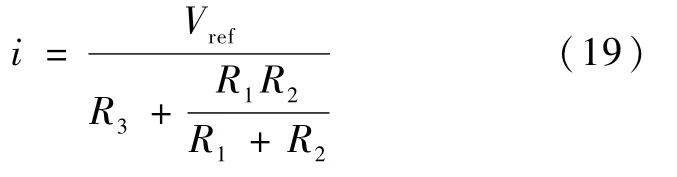
向左流动.由于流经R3和R4的电流相同,故此时电路输出电压

当E=0,由图3(d)电路可知,此时流经R4的电流

向右流动.由于流经R3和R4的电流相同,故此时A点的电位

因此流经R1的电流为
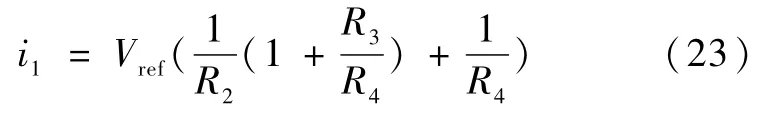
由V=i1R1+VA得

令图3(a)、(b)中相应的截距相等得

将式(25)改写成

式(26)和(27)的右侧均为已知数.选定

则式(26)和(27)有3个比值R1/R2,R3/R4和R1/R4待定.将这两式联列解得

式(29)与(18)相同.因比值R3/R4>0,故由式(30)得

满足上式的比值R1/R4,均可用来构成V/E转换电路.现取

将上式代入式(30)得

式(29)、(32)、(33)给出图3(d)中各电阻应满足的条件.
3 两个设计例子
设定一次电源电压80V时直流变换器运行频率fmax=300kHz,120V时运行频率fmin=200 kHz,故比值fmax/fmin=1.5.选定用1843A来构造变频式脉宽调制器.由表1(b)知,当选择RT=2kΩ,E在4~6V变化时可实现这个频率比值.在图2中RT= 2 kΩ的曲线上选定E=5.80的点p1作为fmax= 300kH z工作点,p1点的F值为1.74.根据式(5), fmin=200kH z工作点的F值应为

在RT=2 kΩ的曲线上找到F=1.16的点p2,其E值(即E2)为4.24.至此我们得到数据:V1=80V, V2=120V,E1=5.80V,E2=4.24V.取Vref=5.0V,它满足式(16).取R2=10 kΩ,将以上数据代入公式(17)和(18)得

将RT=2 kΩ,F(5.80,2×103)=1.74,f(5.80,2× 103)=300 kHz代入式(3)得

图4(a)示出这个设计电路.
现计算图4(b)中各电阻的值.将数据 V1= 80V,V2=120V,E1=5.80V,E2=4.24V,Vref=5.0V, R2=10kΩ代入式(29)(32)(33)得R1=191kΩ, R3=9.5kΩ,R4=14.90kΩ.

图4 构造变频式脉宽调制器Fig.4 Constructing a frequency-modulated pulse-width modulator
4 实验结果
现选用一般脉宽调制器 UC1843A和放大器LM648构造图4(a)和(b)的实验电路.首先测量UC1843A中振荡器参数VL,VH和i的值.VL和VH由图4中UC1843A⑥脚电压波形的最低值和最高值测得,它们与标称值一致.i由⑥脚引线电流波形的幅值测得,它与标称值一致.选用十圈电位器构成R1,R2,R3, R4,RT,调节其阻值精确到计算值的末位,CT值为2917pF.所得实测结果如表2所示,它与计算结果一致.

表2 UC1843A的实测与理论数据Tab.2 Measured and theoretical data of UC1843A
5 结 论
本文提出为直流变换器增设一个控制变量的思路,解决了将一般脉宽调制器184X和184XA构造成变频式脉宽调制器的有关问题.
本文的实验证实在参考文献[1]中提出的计算184X和184XA振荡频率和占空比的公式(1)和(2)是正确的.本文所述电压(E/V)线性转换电路,其解析方法与以往所见文献不同,我们称为“截距法”,可推广用于解析其他形式的电压线性转换电路.
[1] 孙定浩.脉宽调制器中一类振荡器的全面解析结果[J].空间控制技术与应用,2011,37(5):26-30 Sun D H.Completely analytical results of a kind of oscillators in pulse width modulators[J].Aerospace Control and Application,2011,37(5):26-30
[2] Unitrode.Product&applications handbook[M].1993-1994(5):179-191
A Variable Frequency Type of Pulse W idth M odulator Constructed of Using General Pulse W idth M odulator
SUN Dinghao1,ZHAO Changchun2
(1.Beijing Institute of Control Engineering,100190,China;2.Beijing Shengye Science and Tech.Development Co.Ltd,100190,China)
In order to remedy some defects caused by only one regulating variable in the current DC/DC converters,a new concept to add a control variable in the converters is proposed.In this paper,the chosen control variable is the operating frequency f of the converter,and make f decrease according to a set law when the voltage of the primary power supp ly increases,so as to solve some problems such as severe heating of the switching transistors,etc.when the frequency is invariable.The main problem to realize the idea is to construct a variable frequency type of pulse width modulator(PWM)by a general PWM. Now taking the general modulator 1842/3/4/5 and 1842A/3A/4A/5A as examples to discuss how to construct the variable frequency type of PWM,and show the realizable frequency characters are given. Both of the linear transform circuits of voltages are designed to transform the voltage of the primary power supply to the input voltage of the PWM.The representations for calculating parameters of elements in these circuits are derived.The experiment results are consistent with designs.
variable frequency type of pulse width modulator;linear transfer circuits of voltages
TM13
A
1674-1579(2012)01-0040-06
10.3969/j.issn.1674-1579.2012.01.007
孙定浩(1934-),男,高级工程师,研究方向为电功率变换技术;赵长春(1976-),男,工程师,研究方向为电功率变换技术.
2011-08-01
