基于双二体模型的月球探测器返回轨道初步设计及特性分析
2012-09-05周亮,胡军
周 亮,胡 军
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
研究论文
基于双二体模型的月球探测器返回轨道初步设计及特性分析
周 亮1,2,胡 军1,2
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
双二体模型是深空探测初步轨道设计普遍采用的假设.本文针对月球探测器从月球驻留轨道返回的任务,对直接返回型轨道和间接返回型轨道,建立了基于直观六参数的返回轨道模型.通过对直观六参数及出口点时刻这些可选参数的分析,得到了约束条件和可选参数的定性关系,易于搜索满足要求的返回轨道.最后针对两种返回轨道类型的算例表明该方法是有效的.
返回轨道;初步设计;特性分析;直观六参数
轨道设计与特性分析一直是深空探测领域内一个重要的研究方向,轨道设计的优劣直接关系到航天使命能否顺利完成[1].月球采样返回是月球探测任务中的重要内容[2],对于返回轨道的研究无疑具有重要的意义.
一般基于双二体模型,采用圆锥曲线拼接法进行轨道的初步设计.对飞行任务的初步分析方法,在月球影响球的边缘将两个圆锥曲线轨道拼接在一起的简便方法是一种相当好的近似方法[3].对于深空探测的轨道设计来说,利用初步轨道设计得到的初值尤其重要,它直接影响到精确轨道设计中数值计算的复杂性和收敛性.利用较精确的轨道初值,能够大大缩短搜索精确轨道设计参数所需的时间和迭代次数,初值选择不恰当很容易导致精确轨道设计中参数的不收敛.另外在初步设计阶段,只需考虑影响探测器运动的主要因素,在合理的假设基础上根据简单的表达式分析计算.经大量计算,定性分析各种转移轨道的特性,有利于抓到影响轨道特性的主要因素,这对实际轨道设计有重要的指导意义.
本文在文献[4]的基础上,针对直接返回型轨道和间接返回型轨道,采用双二体理论模型,提出了直观六参数返回轨道初步设计方法.新选择六个独立参数,物理意义明晰,可直接得到月心段轨道参数,方便在出口点轨道拼接.利用简单且解析的计算公式,可初步设计返回轨道,并分析直观六参数以及出口点时刻对轨道特性的影响,得到一些定性的结论.针对提出的方法,对应两种返回轨道类型,分别给出较节省燃料的返回轨道初步设计算例,并进行了比较.
1 月球探测器返回轨道初步设计模型
本文所指的返回轨道是指从月球驻留轨道出发,经深空遨游,到达地球驻留轨道,或地球大气再入点的轨迹.采用双二体模型,即在返回过程中,在月球影响球内只受月球引力的影响,其月心段轨迹为双曲线;在月球影响球外只受地球引力的影响,其地心段轨迹为椭圆.
研究从月球驻留轨道出发的两种类型的返回轨道,即直接返回型轨道和间接返回型轨道,分别如图1和图2所示.直接返回型轨道只需在月球驻留轨道实施一次变轨,在返回轨道终端需满足再入点的约束条件,直接再入大气,节省了燃料,但对GNC系统提出了更高的要求,增大了对返回窗口的限制.间接返回型轨道还需在返回轨道的终端即近地点处实施一次变轨,形成地球驻留轨道,加大了对速度增量的需求,但有利于提高返回任务的可靠性,同时为探测器与空间站的交会对接提供了可能.
1.1 坐标系的建立和直观六参数的选取
建立月心近焦点坐标系OL-pqw,探测器月心段轨道面为基本平面,月心OL为坐标系原点,OLp轴由月心指向加速点,OLw轴垂直轨道面,方向与探测器角动量方向一致,OLq轴在轨道面满足右手法则.月心白道坐标系OL-xyz取探测器离开月球影响球瞬时的白道面为基本平面,月心OL为坐标系原点,OLx是该时刻月心指向地心的方向,OLz轴垂直白道面,方向与探测器角动量方向一致,OLy在白道面满足右手法则.OL-xyz为惯性空间保持方向不变的坐标系[5].将OL-xyz原点OL平移至地球中心OE,方向不变,形成地心白道坐标系OE-xyz.地心赤道坐标系OE-XYZ,即常用的地心J2000平赤道坐标系,地心OE为原点,OEX在赤道面内指向春分点,OEZ垂直于赤道平面,与地球自转轴重合,指向北极,OEY在赤道面满足右手法则.
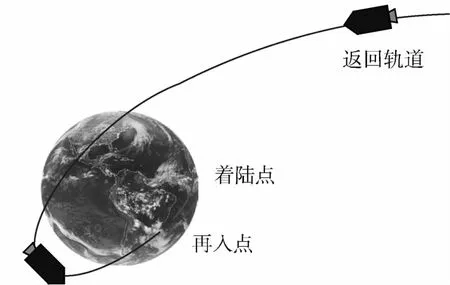
图1 直接返回型轨道示意图Fig.1 Sketch of direct return trajectory

图2 间接返回型轨道示意图Fig.2 Sketch of indirect return trajectory
图3 显示了返回轨道在出口点时的几何关系,只包含了升段出口的情况,对于降段出口情况,分析方法一致,不再论述.选取探测器月球驻留轨道高度hL,驻留轨道的倾角iL,出口点和月球的连线与地月连线的夹角δ,出口点纬度φ及出口点时月心真近点角fCL以及加速点航迹角βAL作为独立参数.显而易见,利用此直观六参数可直接求出月心段轨道的参数.
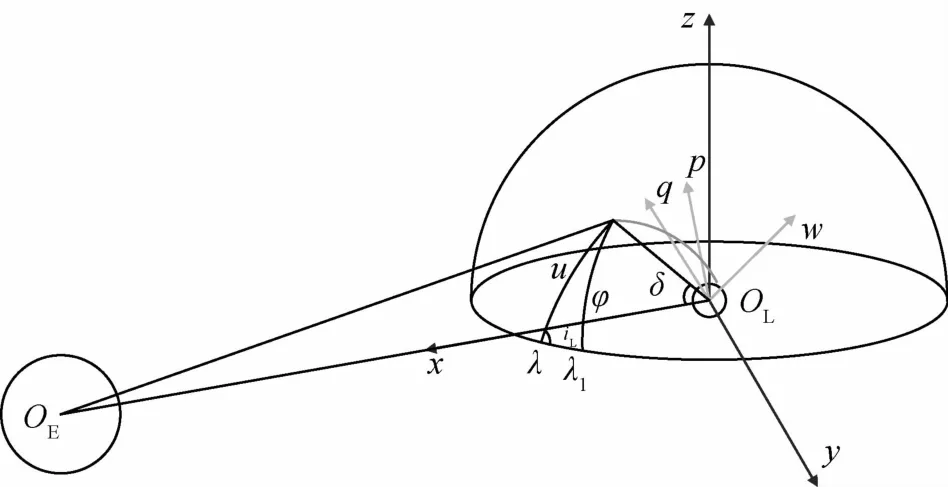
图3 月球探测器出口点示意图Fig.3 Sketch of outlet point
1.2 月心段轨道参数的求取利用
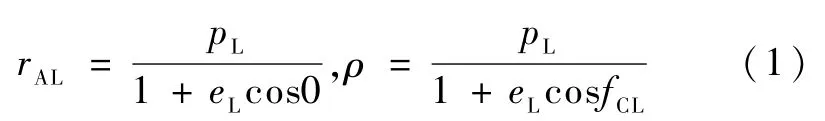
可求出月心段轨道的半通径pL和偏心率eL.其中rAL为加速点的月心距,ρ=66200km表示月球影响球半径.继而容易求出月心段半长轴aL和月心段轨道飞行时间TCL.
在坐标系OL-pqw下,加速点速度矢量vAL为
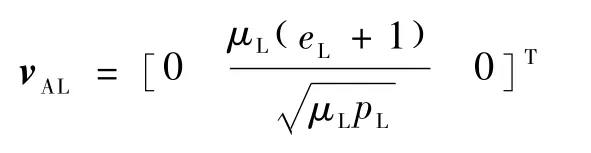
其中μL为月球引力常数.
所以加速点所需的速度增量ΔvA
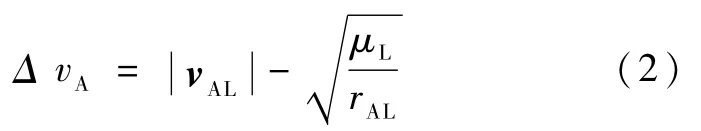
1.3 出口点位置矢量与速度矢量的求取
在坐标系OL-pqw下可得出口点相对月心的位置矢量rCL和速度矢量vCL如下:
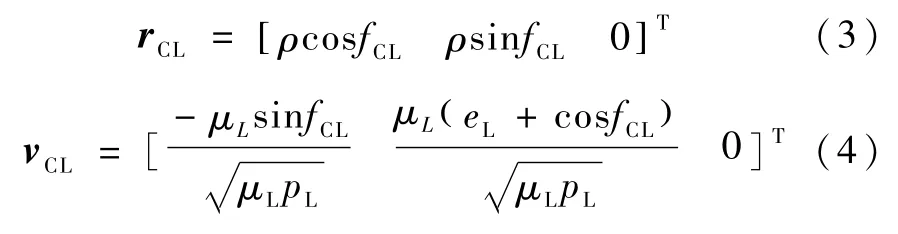
如图3所定义,根据球面三角形公式可知
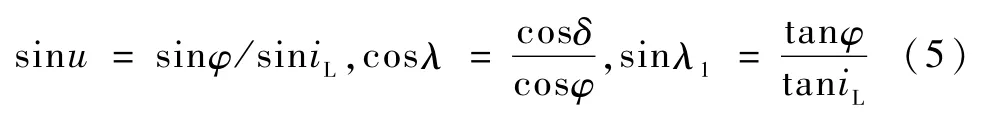
由几何关系可得,月心段轨道的升交点经度ΩL和近月点幅角ωL为
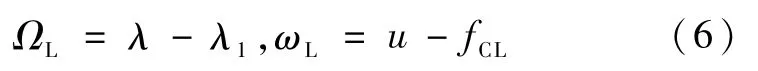
利用坐标系变换,可得在OL-xyz坐标系内的位置矢量RCL和速度矢量VCL,以及加速点的位置矢量RAL和速度矢量VAL:
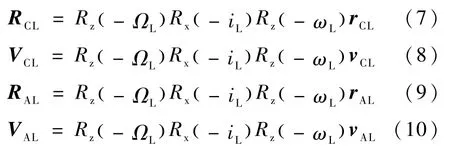
其中rAL=rAL[ ]0 0T.
根据双二体假设,月球绕地球以384400km为半径作圆周运动.则月球位置矢量REL和速度矢量VEL分别为

由此可得出口点相对地心的位置矢量RCE和速度矢量VCE
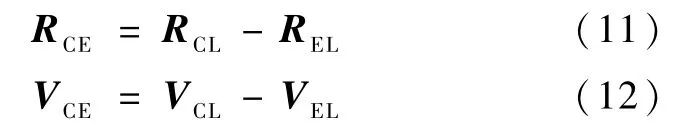
1.4 地心段轨道参数的求取
由RCE和VCE可得OE-xyz坐标系下地心段的轨道根数[6].
对于间接返回型轨道,可得一些重要参数:近地点地心距rE,出口点地心扫角fCE,间接返回型轨道地心段轨道飞行时间TCE,分别为
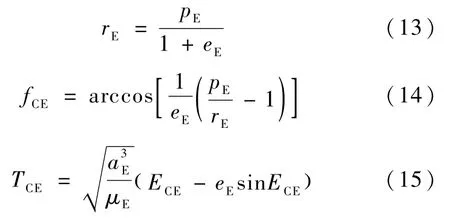
其中ECE满足
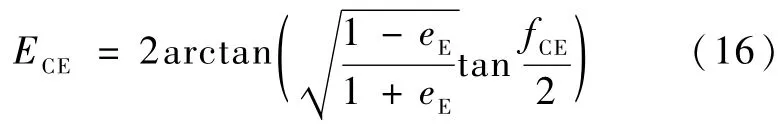
对于直接返回型轨道,再入点地心距rZE与所对应的地心扫角fZE满足
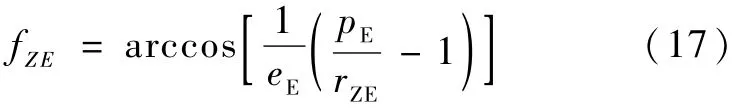
直接返回型轨道地心段飞行时间为
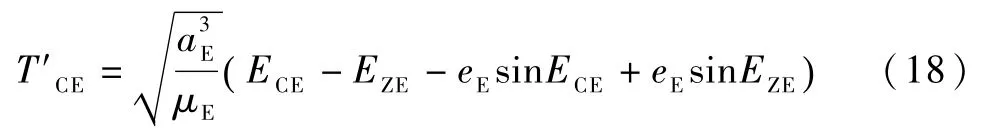
其中EZE满足
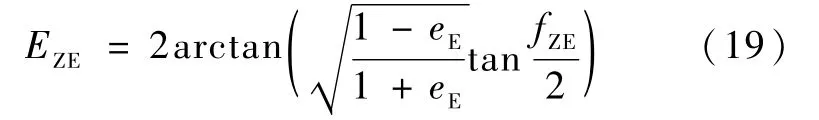
直接返回型轨道要求再入点再入角在 -3°~-8°之间,再入角θ是再入点处速度方向即轨道切向与轨道横向之间的夹角[7],与地心扫角和轨道偏心率有关,如下式所示:
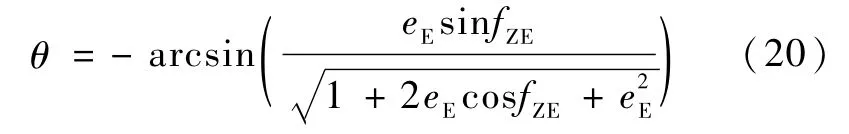
类似求取月心段近月点状态的方法,可得坐标系OE-xyz下近地点的位置矢量RE和速度矢量VE或再入点的位置矢量RZE和速度矢量VZE.
1.5 地心赤道坐标系下参数的求取
由探测器到达出口点的时刻 tC,通过近似公式或JPL的DE405星历[8]都可以得到该时刻月球运行的位置和速度.从而求出地心白道坐标系到地心赤道坐标系的状态转移矩阵M.即在地心赤道坐标系OE-XYZ近地点的位置矢量rE和速度矢量vE
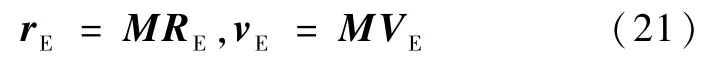
由rE,vE可根据1.4节的方法求得地心段轨道在OE-XYZ下的轨道根数.对于直接返回型轨道位置矢量rZE和速度矢量vZE,以及轨道根数可采用相同的方法得到,此外还需求取再入点的经纬度.
根据rZE可得再入点的赤经θE和纬度φE:
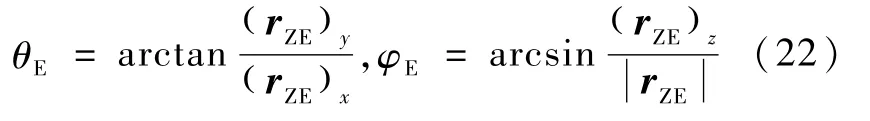
出口点时刻为tC,则到达再入点时刻为tC+ TCE,将再入点时刻世界时化为儒略日JD,J0表示世界时0点的儒略日,UT表示过世界时0点后的小时数,则
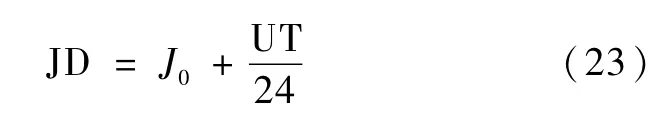
可得到达再入点时格林威治的赤经θGθG=100.4606184+36000.77004T0+
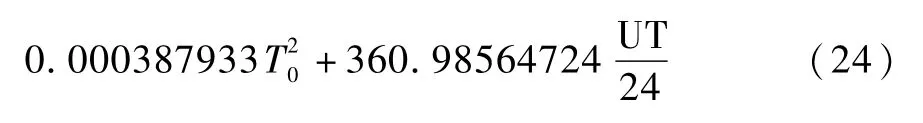
而后可得再入点的经度

下节主要分析直观六参数对返回轨道参数的影响,试图找到直观六参数以及出口点时刻与约束条件之间的定性关系.对于间接返回型轨道,地球端需要满足近地点地心距、轨道倾角的要求,而对于直接返回型轨道,地球端需要满足再入点地心距、轨道倾角、再入角、再入点经度和纬度的约束.
2 轨道特性分析
为得到满足要求的轨道,需要分析直观六参数与约束条件的关系.由于问题的复杂性,定量的关系不可能得到,只有通过分析其中的定性关系,从而确定可选参数,所以必须要进行轨道特性的分析.
由于返回轨道要求是地心顺行轨道(iE≤90°),所以对于iE>90°的情况将不再讨论.对于直观六参数的分析,任选出口点时刻为2015年3月1日 0时 0分 0秒,由于恒星月的平均长度为27.32166平太阳日,所做假设并不失普遍性.
2.1 月球驻留轨道高度的影响
假设:探测器月球驻留轨道倾角iL=40°,出口点和月球的连线与地月连线的夹角δ=70°,出口点纬度φ=-3°,加速点航迹角βAL=90°.要求根据探测器不同的月球驻留轨道高度hL,调整出口点时月心真近点角fCL使得探测器地球驻留轨道地心距rE=6600km.表1给出了探测器不同月球驻留轨道高度对返回轨道的影响.
由表1可以看出:
1)月球驻留轨道高度越高,对应月心真近点角越小,所需速度略有减小,航行时间略有增加;
2)月球驻留轨道高度的变化对地心段轨道倾角基本没有影响,对升交点赤经影响不大;
3)月球驻留轨道高度的变化总体上对探测器轨道特性影响不大.
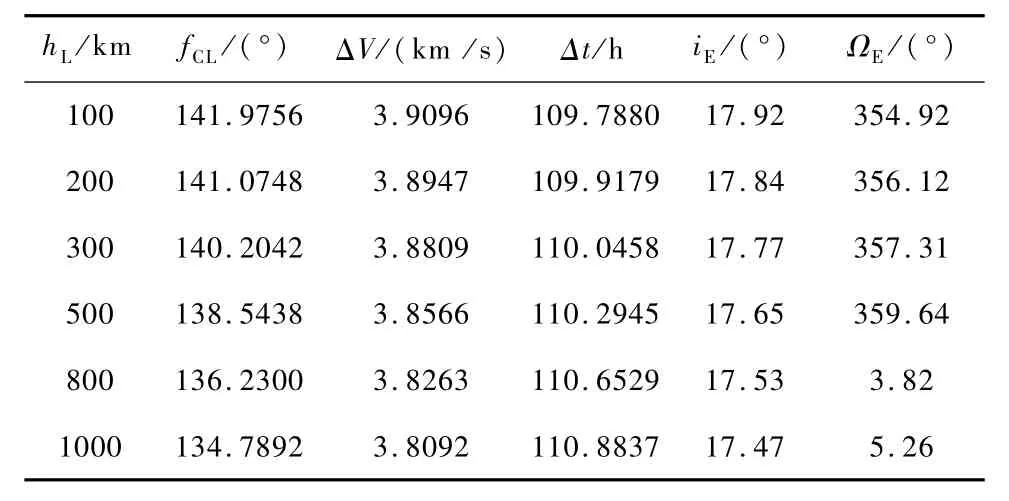
表1 月球驻留轨道高度对返回轨道的影响Tab.1 Effect ofmoon parking orbit altitude on return trajectory
2.2 月球驻留轨道倾角的影响
在介绍完桌上的祭品之后,三位演员开始倒酒,点香烛,跪拜。祖、父、孙三位演员在主持人的介绍下先后走到桌边,双手合十面朝外跪拜三次,后又起立拜了三次。跪拜完毕,就是散福。据主持人介绍,按照传统,散福就是家人一起吃用鸡、鹅的汤汁烧的年糕,而在景区就以花生替代了。主持人的一句“大家把干果放在口袋里,就是把福带回家了”引来游客纷纷索要花生。刚才的几个演员一把一把地把花生分发给游客,但还是有外围的游客没有拿到。他们争着往里面挤进来,伸着手臂,把围在八仙桌外的护栏带都挤垮了。工作人员只好马上停止散福,游客散去,“祝福”仪式就此结束。
假设:hL=200km,δ=70°,φ=-3°,βAL=90°.要求根据探测器不同的 iL,调整 fCL使得 rE= 6600km.表2给出了探测器不同月球驻留轨道倾角对返回轨道的影响.
由表2可以看出:
1)在合适的出口点参数δ,φ选择后,只需选择合适的fCL就保证对于不同的iL都能返回地球;
2)随着iL的增加,对应fCL逐渐减小,所需速度增量略有增加,航行时间则略有减少;
3)在iL=60°时大致对应最小的iE,但iE对iL的变化不敏感,调节iL可以有效控制ΩE;
4)iL对φE,λE几乎没有影响;
5)iL的变化总体上对探测器轨道特性影响不大.
假设:hL=200km,iL=40°,φ=-3°,βAL= 90°.要求根据探测器不同的δ,调整fCL使得rE= 6600km.表3给出了不同探测器与月球连线和地月连线夹角对返回轨道的影响.
由表3可以看出:
1)随着δ的增加,对应fCL大幅度增加,飞行时间单调递增,所需速度增量先迅速减小,而后略有增大,即存在最小的速度增量.对于本例δ=74°所需速度增量最小.表明 δ的选择不仅决定月球探测器所需要的速度增量,也可以决定飞行时间,这与文献[9]所得到的结论一致;
2)存在δ的盲点,即在这些夹角情况下,不能完成返回轨道的设计;
3)δ对iE,ΩE和φE,λE都有一定程度的影响.通过调节δ,可以对iE,ΩE和φE,λE进行细调;
4)δ是返回轨道设计中重要的调节参数.
2.4 出口点纬度的影响
假设:hL=200km,iL=40°,δ=70°,βAL= 90°.要求根据探测器不同的φ,调整fCL使得rE= 6600km.表4给出了探测器不同出口点纬度对返回轨道的影响.
由表4可以看出:
1)随着φ的增加,所需速度增量先减小,而后略有增大,即存在最小的速度增量,对于本例 φ= -3°所需速度增量最小;
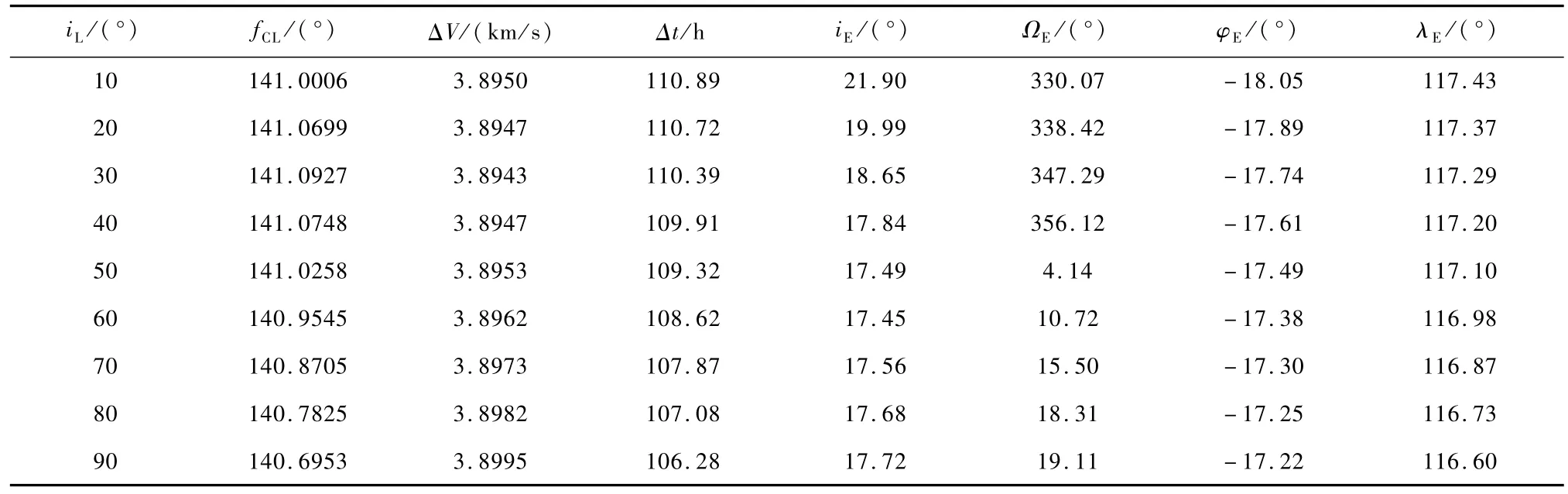
表2 月球驻留轨道倾角对返回轨道的影响Tab.2 Effect ofmoon parking orbit inclination on return trajectory
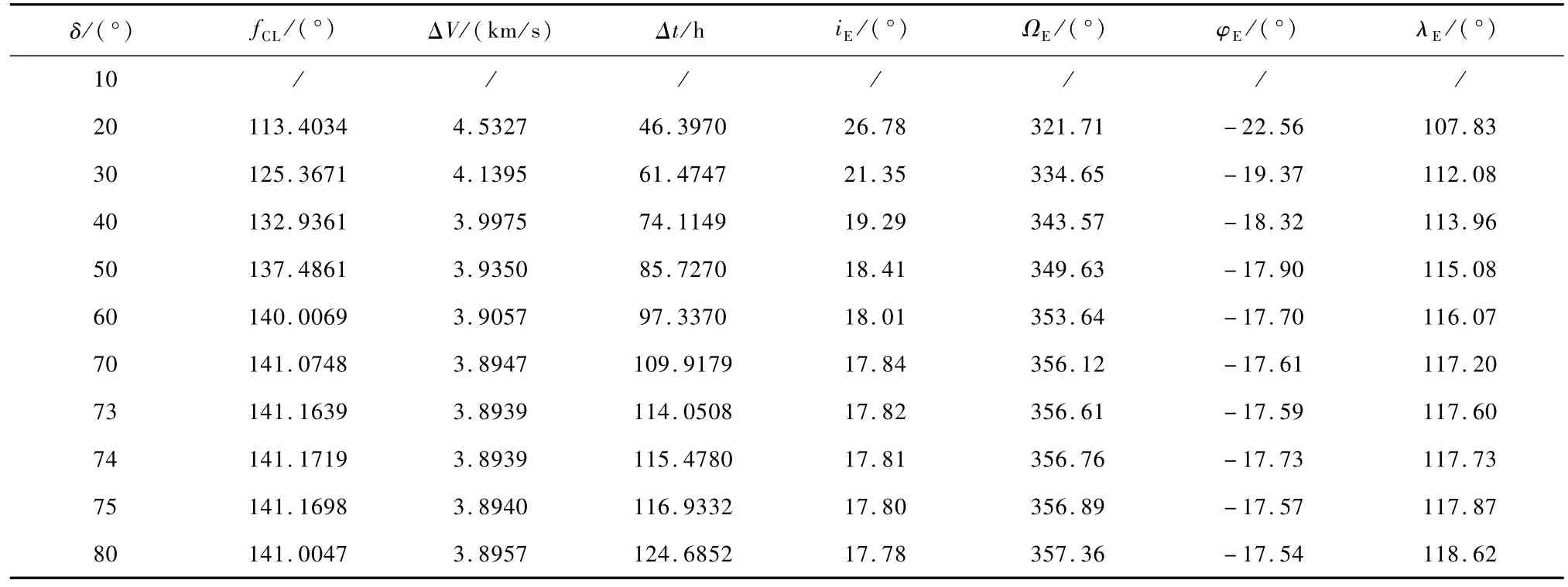
表3 探测器与月球连线和地月连线夹角对返回轨道的影响Tab.3 Effect of angle between probe-moon line and earth-moon line on return trajectory
2)存在 φ的盲点,即在这些出口点纬度情况下,不能完成返回轨道的设计;
3)iE,ΩE对φ的变化很敏感,从而通过调整φ可以调整iE和ΩE;
4)φ对φE,λE几乎没有影响.
2.5 出口点时月心真近点角的影响
假设:hL=200km,iL=40°,δ=70°,φ= -3°,βAL=90°.表5给出了探测器不同出口点时月心真近点角对返回轨道的影响.
由表5可以看出:
1)探测器地球驻留轨道高度hE随着fCL增加而增加,所需的速度增量越少,飞行时间越长,但变化并不明显,所以调整地球驻留轨道高度的主要参数是fCL;
2)iE,ΩE和φE,λE对地球驻留轨道高度的变化不敏感;
3)月心真近点角的微小变化都会使探测器地球驻留轨道高度发生较大的变化,这对于深空测控和轨道控制提出了更高的要求.
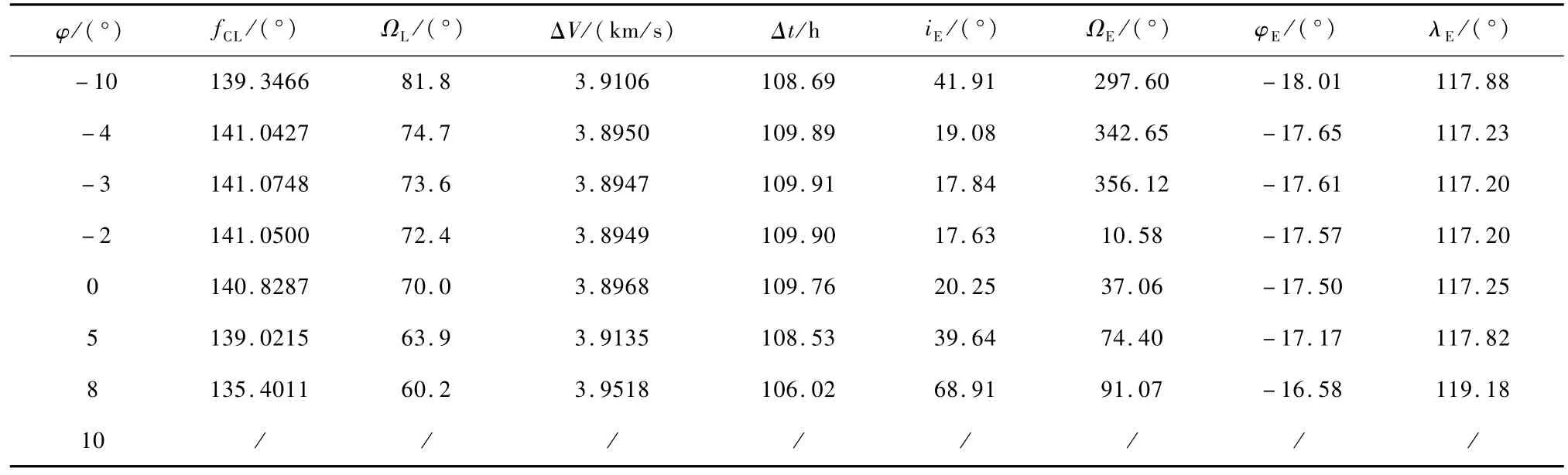
表4 探测器出口点纬度对返回轨道的影响Tab.4 Effect of outlet point latitude on return trajectory
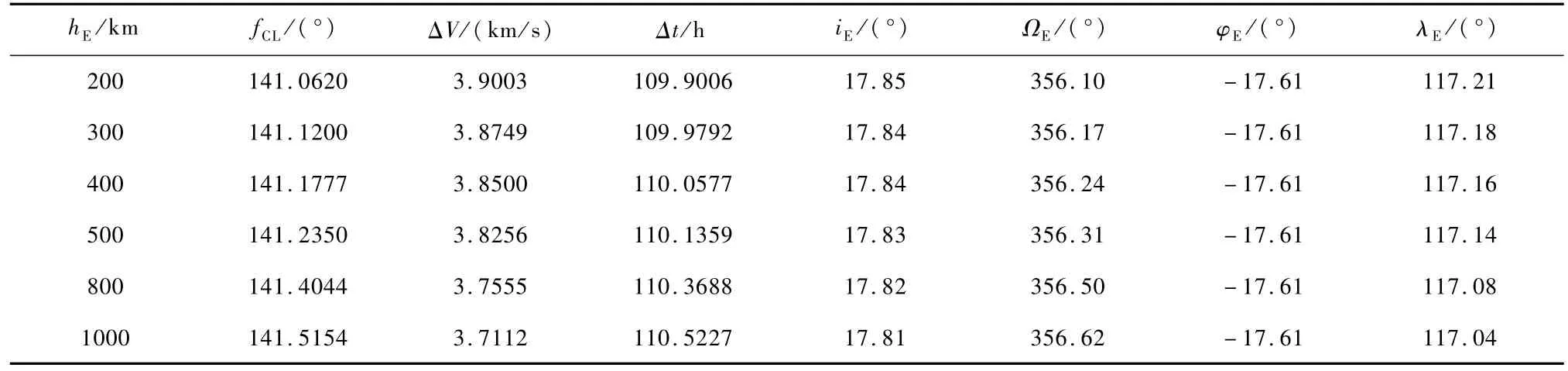
表5 出口点时月心真近点角对返回轨道的影响Tab.5 Effect of outlet point true anomaly on return trajectory centered in themoon
2.6 加速点航迹角的影响
利用动量矩守恒可得
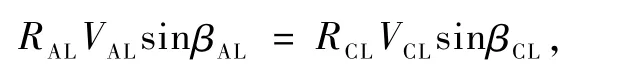
根据其他轨道要素可确定加速点RAL以及出口点RCL,VCL和βCL,所以要使得加速点所需VCL最小,应使βAL=90°,即探测器在月球驻留轨道上加速的方向和探测器的速度方向一致.事实上,工程上大都采用这样的加速方案,以保证加速所需能量较小.
2.7 出口点时刻的影响
首先分析出口点时刻对间接返回型轨道的影响.假设:hL=200km,iL=40°,δ=73.6°,φ=3° ,fCL=140.1178,βAL=90°.此时rE=6600km.图4给出了2015年3月间接返回型轨道地心段轨道倾角随出口点日期变化的曲线.
下面考察出口点时刻对直接返回型轨道的影响.假设:hL=200km,iL=40°,δ=73.6°,φ=3°, fCL=140.0039,βAL=90°.此时 rZE=6500km, θ=-6°.图5给出了2015年3月直接返回型轨道地心段轨道倾角随出口点日期变化的曲线,图6给出了再入点经纬度随出口点日期变化的曲线.
对于间接返回型轨道,从图 4可以看出:不同的出口点时刻对应不同的 iE,从而可通过调整出口点时刻调整iE.对于直接返回型轨道,从图5和6可以看出:不同的出口点时刻对应不同的iE,同时出口点时刻的变化对 φE,λE影响很大,从而可通过调整出口点时刻调整 iE和 φE,λE.需要说明的是,由于采用的双二体模型,对条件进行了简化,所以不同的出口点时刻对速度增量和飞行时间没有影响.
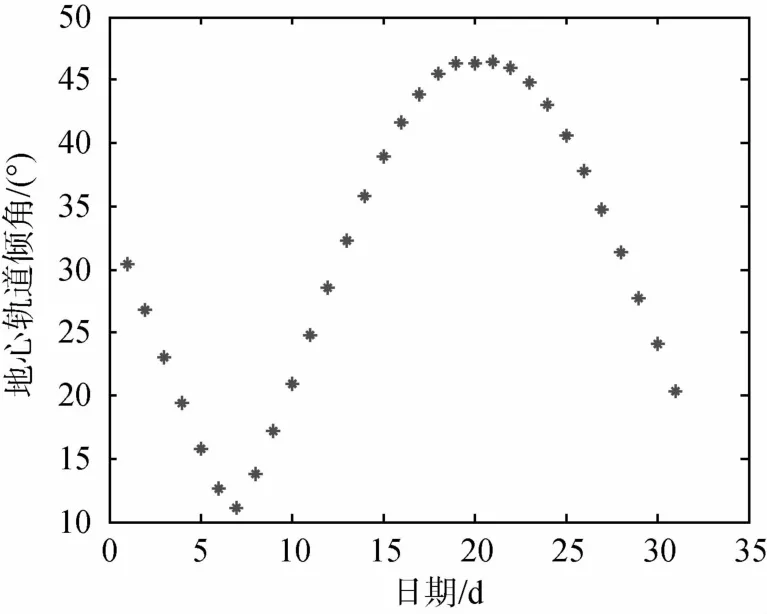
图4 间接返回型轨道出口点时刻对地心段轨道倾角的影响Fig.4 Relation between inclination centered in the earth and time of outlet point at indirect return trajectory
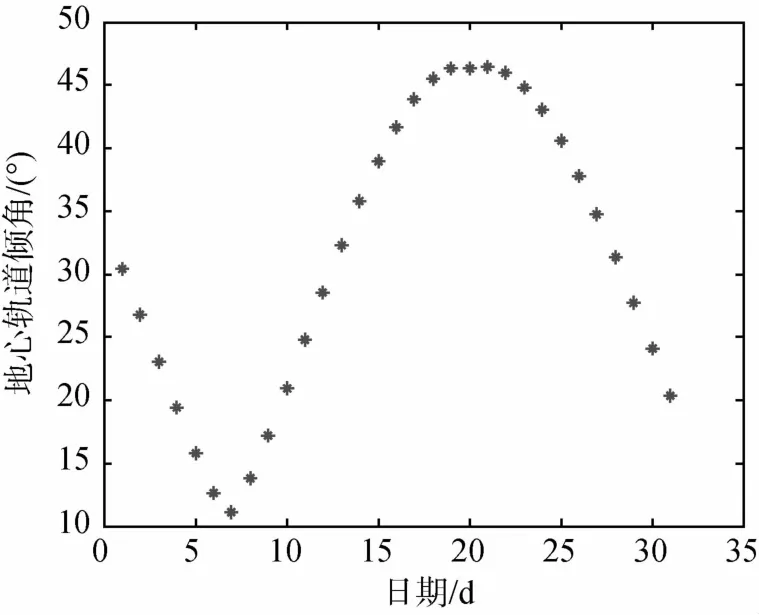
图5 直接返回型轨道出口点时刻对地心轨道倾角的影响Fig.5 Relation between inclination centered in the earth and time of outlet point at direct return trajectory

图6 直接返回型轨道出口点时刻对地心纬度、经度的影响Fig.6 Relation between latitude,longitude centered in the earth and time of outlet point at direct return trajectory
2.8 返回轨道设计流程
双二体轨道设计实质上是要找出合适的出口点和出口点状态,使探测器在两个中心引力体的分别作用下,满足特定月球探测任务的约束条件.通过分析直观六参数以及出口点时刻对返回轨道特性的影响,可得以下结论:
1)通过调整出口点时刻可对iE,ΩE和φE,λE进行粗调;
2)通过调整iL可有效控制ΩE;
3)通过调整δ,可对iE,ΩE和φE,λE进行细调;
4)通过调整φ可对iE和ΩE进行细调,而几乎不影响φE,λE;
5)通过调整fCL可调整hE,从而可选择合适的θ.
间接返回型轨道和直接返回型轨道初步设计的设计流程图如图7、8所示.
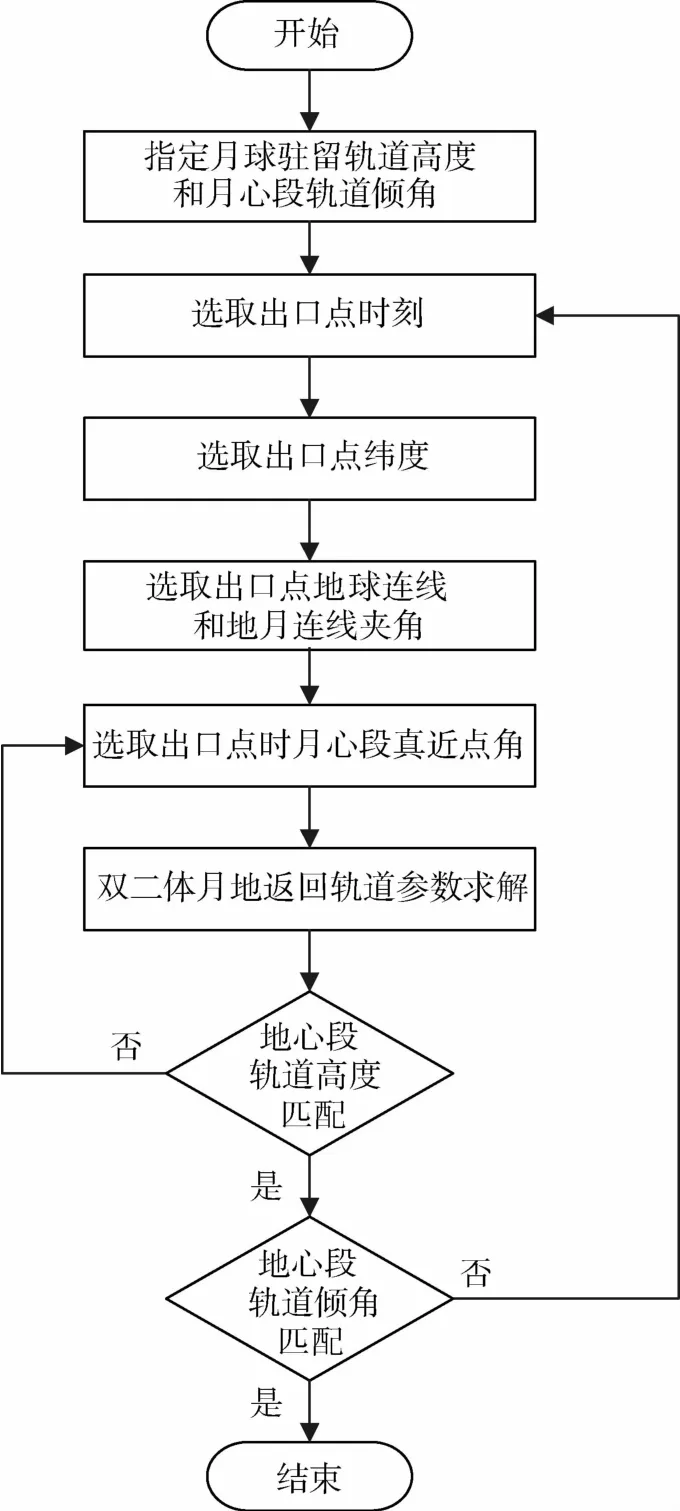
图7 间接返回型轨道初步设计流程图Fig.7 Flow chart of preliminary design of indirect return trajectory
3 轨道初步设计算例
对于返回轨道类型和具体的约束条件如表6所示.对于间接返回型轨道,可选参数值如表7所示.对应的月心段参数和地心段参数分别如表8和9所示.对于直接返回型轨道,可选参数值如表10所示.对应的月心段参数和地心段参数分别如表11、12所示.得到的返回轨道仿真图如图9所示.本着节省能量的要求,δ选择在70°左右,φ选择在0°左右,fCL选择在140°左右,这些参数范围的确定对于参数的搜索是十分有利的.同时由轨道特性的分析结果可知,在这些范围选择参数可以得到较省能量的轨道设计结果.参数的搜索选择分层穷举法,利用定性分析的轨道特性结论,设定合适的搜索初值和较小的搜索范围可以有效降低搜索的时间.由于可选参数选择类似,两种类型的返回轨道得到的轨道参数非常接近.但从能量角度出发,采用直接返回型轨道所需的速度增量仅是间接返回型所需速度增量的1/5左右.间接返回型轨道则可实现在近地轨道的交会对接等任务.
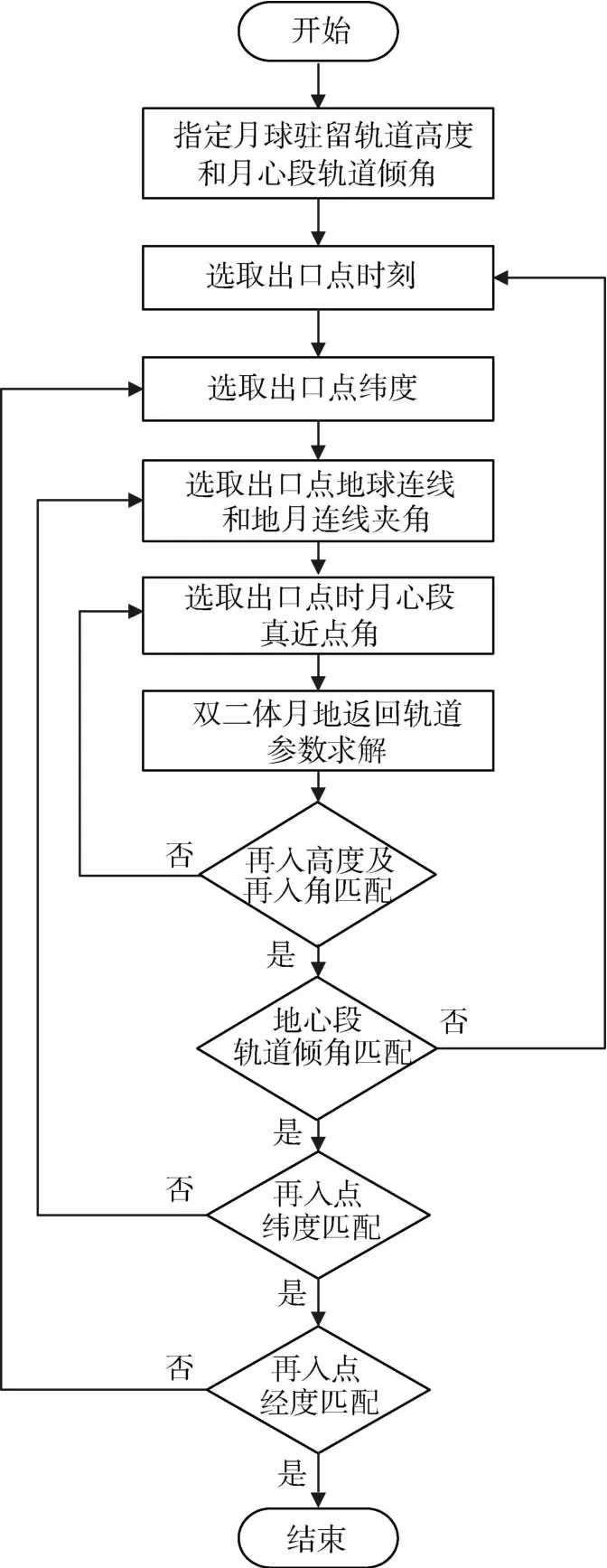
图8 直接返回型轨道初步设计流程图Fig.8 Flow chart of prelim inary design of direct return trajectory

图9 直观六参数返回轨道初步设计图Fig.9 Sketch of preliminary design of return trajectory using six independent parameters

表6 返回轨道的约束条件Tab.6 Constraints of return trajectory

表7 间接返回型轨道参数Tab.7 Parameters of indirect return trajectory

表8 间接返回型轨道月心段参数Tab.8 Parameters of indirect return trajectory centered in themoon

表9 间接返回型轨道地心段参数Tab.9 Parameters of indirect return trajectory centered in the earth

表10 直接返回型轨道参数的选取Tab.10 Parameters of direct return trajectory
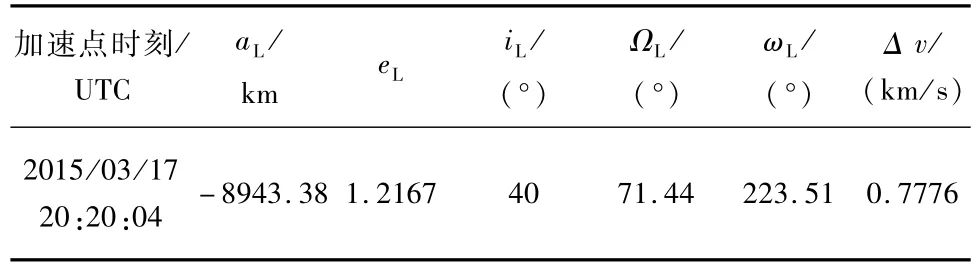
表11 直接返回型轨道月心段参数Tab.11 Parameters of direct return trajectory centered in the moon

表12 直接返回型轨道地心段参数Tab.12 Parameters of direct return trajectory centered in the earth
4 结 论
利用本文所提出的直观六参数法求解初步轨道,直观、简单,可直接得到轨道参数,避免了复杂方程的求解.同时,选择的各物理量意义明显,有利于对于轨道特性的分析,根据得到的定性结论,易于搜索满足约束条件的轨道.针对两种返回类型轨道的算例表明该方法是有效的.
[1] Wertz J R,Larson W J.Space m ission analysis and design[M].EL Segundo,USA:Microcosm Press, 1999
[2] 韩鸿硕,陈杰.21世纪国外深空探测发展计划及进展[J].航天器工程,2008,17(3):1-22 Han W S,Chen J.21st century foreign deep space exploration development plans and their progress[J]. Spacecraft Engineering,2008,17(3):1-22
[3] Bate R R,Mueller D,White JE.Fundamental of astrodynamics[M].New York,USA:Dover Publications, 1971
[4] 白玉铸.月球探测器轨道特性分析[D].长沙:国防科技大学,2005 Bai Y Z.Characteristic analysis of lunar probe trajectory[D].Changsha:National University of Defense Technology,2005
[5] 郗晓宁,曾国强,任萱,等.月球探测器轨道设计[M].北京:国防工业出版社,2001 Xi X N,Zeng G Q,Ren X,et al.Orbit design of lunar probe[M].Beijing:National Defense Industrial Press, 2001
[6] Curtis H D.Orbitalmechanics for engineering students[M].Oxford,UK:Elsevier Butterworth Heinemann, 2005
[7] 赵玉晖,侯锡云,刘林.月球返回轨道再入角变化特征[J].飞行器测控学报,2010,29(5):75-79 Zhao Y H,Hou X Y,Liu L.Characteristics of the reentry angle of lunar probes[J].Journal of Spacecraft TT&C Technology,2010,29(5):75-79
[8] 周文艳,杨维廉.月球星历的计算方法及比较[J].航天器工程,2002,11(4):22-28 Zhou W Y,Yang W L.Computation methods and comparison ofmoon ephemeris[J].Spacecraft Engineering, 2002,11(4):22-28
[9] 林胜勇,李珠基,和兴锁.月球探测器转移轨道特性[J].导弹与航天运载技术,2004,(3):7-12 Lin S Y,Li Z J,He X S.Some characteristics of translunar trajectory[J].Missiles and Space Vehicles, 2004,(3):7-12
[10] 张磊,于登云,张熇.直接再入大气的月球返回轨道设计研究[J].航天器工程,2010,19(5):50-55 Zhang L,Yu D Y,Zhang H.Design of moon return trajectory with direct atmospheric reentry[J].Spacecraft Engineering,2010,19(5):50-55
Return Trajectory Prelim inary Design and General Characteristic Analysis of Idealized Double Two-Body M odel-Based Lunar Spacecraft
ZHOU Liang1,2,HU Jun1,2
(1.Beijing Institute of Control Engineering,Beijing 100190,China;2.Science and Technology on Space Intelligent Control Laboratory,Beijing 100190,China)
Idealized double two-bodymodel is the universal hypothesis in the preliminary trajectory design of deep space.Based on this hypothesis,a return trajectory model with six independent parameters of lunar spacecraft from parking moon orbit including direct return trajectory and indirect return trajectory is designed.Through analysis of the six independent parameters and the time of outlet point,general relationships between constraint and free parameters are given to easily search certain trajectories.Finally, effectiveness of the proposed approach is validated by examples including two types of return trajectory.
return trajectory;preliminary design;general characteristic analysis;six independent parameters
V44
A
1674-1579(2012)01-0001-09
周 亮(1984-),男,博士研究生,研究方向为航天器轨道设计与制导研究;胡 军(1963-),男,研究员,研究方向为航天器制导、导航与控制系统设计与仿真,智能控制、自适应控制理论及其在航天领域中的应用.
2011-09-14
DO I:10.3969/j.issn.1674-1579.2012.01.001
