卫星编队飞行有限时间控制方法*
2012-09-05曾国强
胡 敏,曾国强
(1.中国人民解放军装备学院,北京101416;2.国防科技大学航天与材料工程学院,长沙410073)
卫星编队飞行有限时间控制方法*
胡 敏1,曾国强2
(1.中国人民解放军装备学院,北京101416;2.国防科技大学航天与材料工程学院,长沙410073)
针对卫星编队飞行相对位置控制问题,提出了一种有限时间控制方法.首先,建立了编队卫星相对运动的非线性动力学方程.其次,设计了有限时间快速收敛的滑模面,提出了一种有限时间控制方法,该方法能保证闭环控制系统的全局稳定性和快速收敛性,并给出了理论证明.最后,将提出的方法应用于卫星编队飞行维持控制.仿真结果表明该方法在收敛时间和控制精度方面均优于传统线性滑模控制和终端滑模控制.
卫星编队飞行;有限时间控制;滑模控制;编队维持
提高航天器系统的可靠性和实现系统功能的灵活扩展,是目前整体式大型航天器难以破解的难题.分布式卫星系统技术的发展,例如分离模块集群航天器概念的提出,可以实现多任务载荷以及载荷的升级换代,提高系统的灵活性和可靠性,在完成快速响应空间任务以及遥感与空间探测等领域将发挥重要作用.比较典型的任务是美国国防高级研究计划局于2007年提出的F6计划,模块航天器之间无线连接,进行自由飞行,通过信息交换共同完成特定的任务使命[1].
当分布式卫星系统完成InSAR干涉测高任务时,需要雷达载荷能够快速重构和稳定,同时将卫星之间的基线维持在一定范围.卫星编队飞行技术经过十几年的发展,在编队构形优化设计、高精度相对状态测量、编队协同控制和仿真系统方面都取得了丰硕的成果[2].线性二次型最优控制、自适应控制、滑模控制、模型预测控制以及平均轨道根数都被证明是有效的编队控制方法[3],但是上述方法大多为渐近稳定,没有考虑到有限时间收敛问题,也就是说系统状态会在无穷大的时间才能真正收敛.对于分布式卫星系统完成InSAR任务,系统状态快速收敛和稳定是很关键的.已有研究结果表明,即使存在干扰和不确定性,有限时间控制技术往往能够使闭环系统具有更快的收敛速度和更好的鲁棒性[4].有限时间控制可以通过开环控制方法、非连续反馈控制方法和连续反馈控制方法等实现[5],包括时间最优控制、终端滑模控制、自适应控制、齐次性方法以及有限时间稳定方法等.开环控制的抗干扰能力差,非连续状态反馈会引起系统的抖振,连续有限时间控制技术已经得到了广泛的引用,包括机械臂控制、飞行器姿态控制以及导弹末端导引律设计等[6].
本文针对卫星编队的相对位置控制问题,利用有限时间控制技术设计控制律,该控制律兼顾有传统滑模和终端滑模控制的优点,使得闭环系统同时具有快速的收敛性能和很强的抗扰动性能.仿真结果验证了该方法的有效性和优越性.
1 相对动力学模型
图1中OXIYIZI为地心惯性坐标系,oxyz为卫星之间的相对运动坐标系,即Hill系,x轴指向参考星地心矢径方向,y轴指向参考星速度水平分量方向,z轴和x,y轴构成右手系.
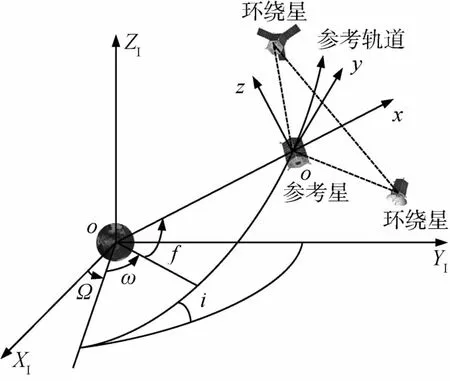
图1 卫星编队飞行示意图Fig.1 Schematic of satellites formation flight
在Hill系中,非线性动力学方程可以表示为[7]
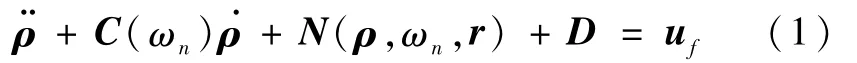
其中:ωn为参考星轨道角速度,D=[D1,D2,D3]T为各种不同摄动力,干扰力以及模型不确定等因素引起的摄动加速度,uf为控制加速度,ρ(t)=[x(t),y(t),z(t)]T为环绕星相对于参考星的位置.
C(ωn)∈R3×3定义如下
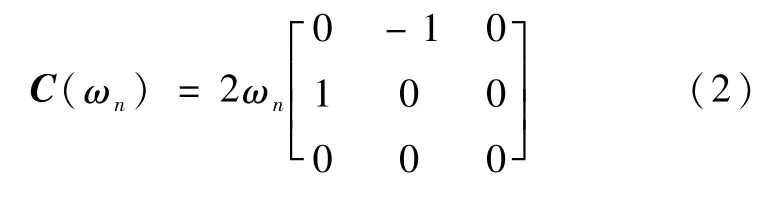
非线性项N(·)∈R定义如下
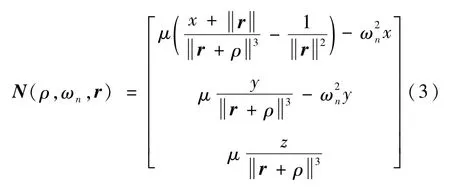
控制的目标就是实现当前相对状态到目标相对状态的跟踪控制,即
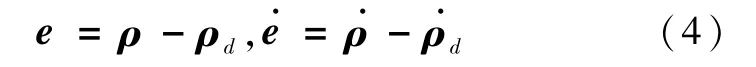
式中ρd和是期望的相对位置和相对速度.
2 控制器设计
2.1 滑模面设计
受文献[8]的启发,将滑模面设计如下
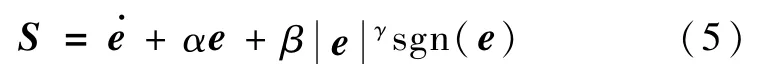
式中α,β>0,0<γ<1.sgn()为符号函数.
2.2 控制律设计
系统控制的目的是在模型具有不确定性和存在外界干扰的情况下,使系统当前的状态跟踪期望状态,并使系统保持稳定且具有良好的动态性能.
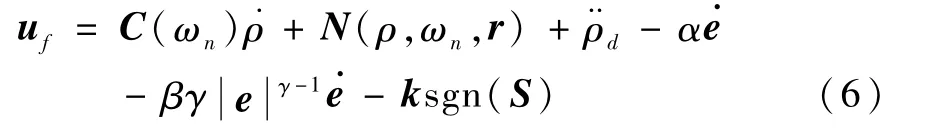
滑模控制律设计如下:如果系统的偏差量较大,线性部分 -αe将起主要作用,使系统具有较快的收敛速度;如果偏差量较小,
式中k=diag{k1,k2,k3}为控制增益矩阵,ki(i= 1,2,3)为正实数.
定理.对于系统(1),在控制律(6)的作用下,系统状态可在有限时间内到达滑模面(5),而且状态量将在有限时间内收敛到零.
证明.(1)先证明系统可在有限时间内到达滑模面
选取Lyapunov函数为

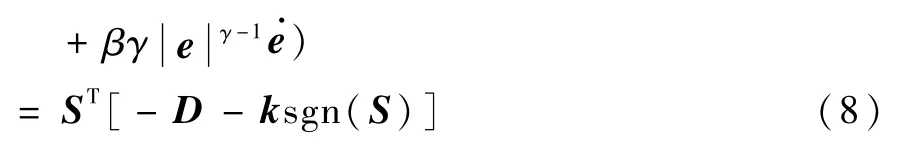
对于近地轨道卫星而言,地球非球形摄动占主导地位,故可以假定扰动 D有界,满足i=1,2,3,其中Fi为一正常数.取控制增益ki>Fi,则
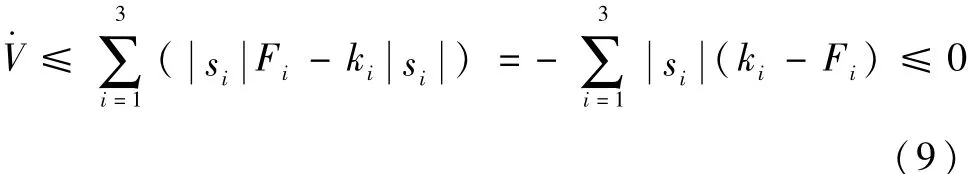
(2)再证明系统可在有限时间内沿滑模面收敛到原点
一旦系统到达滑模面S=0,那么系统运动方程变为:
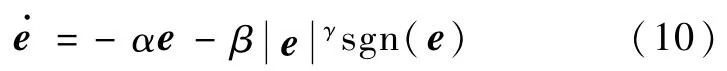
e=0是系统的终端吸引子.通过对式(10)积分,求得在滑模面上的收敛时间为:
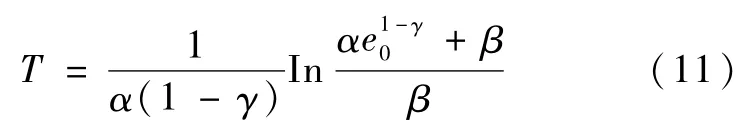
式中In表示自然对数,e0表示x轴,y轴或者z轴的初始状态误差.
可见,一旦系统达到滑模面(5),系统状态将在T时刻收敛到零.
证毕.
注1.对于一般的光滑控制器,为了增强闭环系统的抗扰动性能,只能增大控制增益,考虑到能耗和系统的稳定性,控制增益不宜过大.对于有限时间控制系统,除了可以调节控制增益,还有指数γ可调,在保证控制量不明显增加的情况下,可以使系统具有更高的控制精度,即更强的抗扰动性能.
注2.为了减小变结构系统的抖振现象,通常采用饱和函数来平滑控制量,即
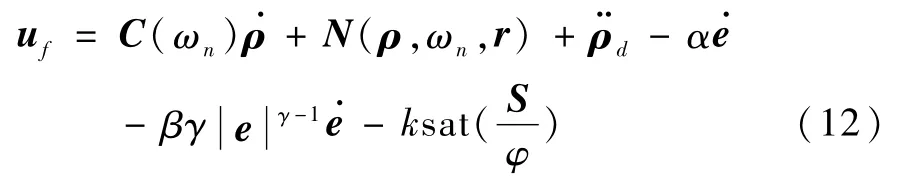
式中sat(·)为饱和函数,定义为
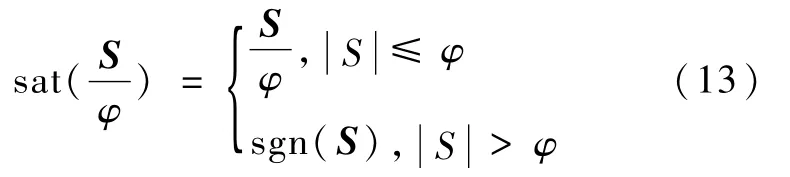
式中φ为边界层的厚度.在边界层外,仍按式(6)进行控制,确保该边界层具有吸引性,在边界层内对uf
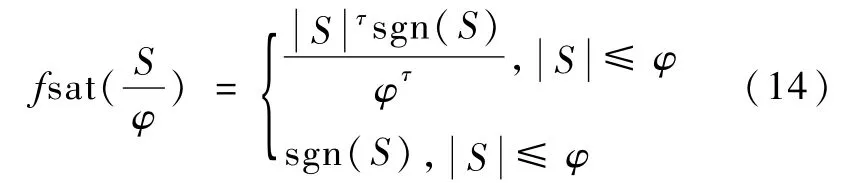
式中0<τ<1.
于是,控制律(12)可以表示为
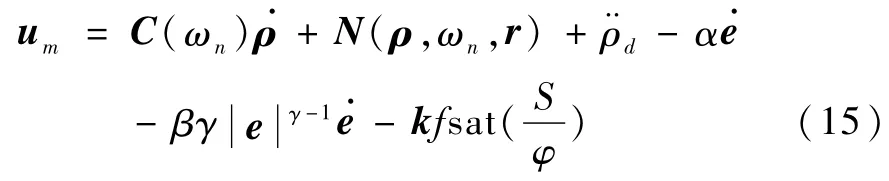
文献[9]证明了采用新的饱和函数(14),系统状态可以在有限时间内收敛到零.
注3.为了测试控制律(15)的有效性,本文还给出了另外两种控制律,分别介绍如下[10-11]:
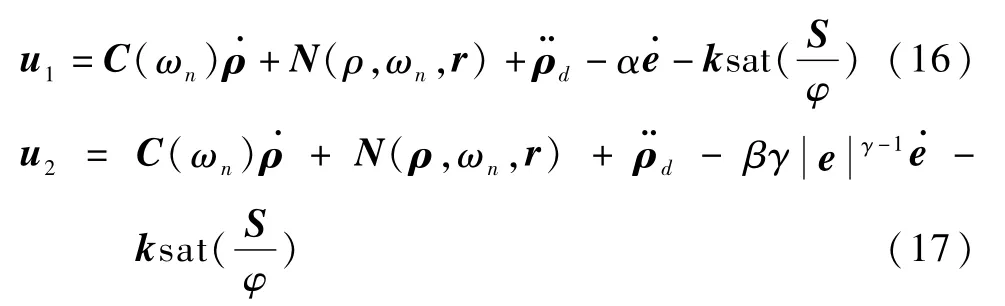
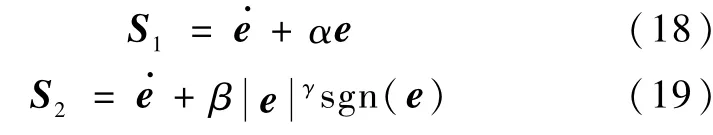
可见,控制律(16)是基于传统线性滑模面的,控制律(17)是一种终端滑模控制器.当初始状态离平衡点较远时,控制律(16)比控制律(17)具有更快的收敛速度;当初始状态离平衡点较近时,控制律(17)比控制律(16)具有更快的收敛速度.本文提出的控制律(15)兼顾有控制律(16)和控制律(17)的优点,能够使系统状态全局快速收敛.
相应的滑模面为:
3 仿真算例与结果分析
参考轨道为近地圆参考轨道,其初始轨道根数如表1所示.

表1 参考轨道初始轨道根数Tab.1 Initial elements of reference orbit
Hill系的初始状态如表2所示.

表2 编队相对状态初始值Tab.2 Initial relative states of formation flying satellites
利用高精度轨道动力学环境进行仿真,考虑地球非球形摄动项、大气摄动、太阳光压摄动、三体摄动以及固体潮摄动,引力场模型为EGM96,大气模型为Jacchia70.采用8阶龙格库塔进行轨道积分,编队维持控制启控误差阈值取为编队构形尺寸的10%,即50m,仿真时间为20000s.控制器(15)中的参数取值为α=[0.01,0.01,0.01]T,β=[0.01,0.01,0.01]T, γ=0.6,k=[0.96,0.96,0.96]T,φ=1.
图2给出了编队卫星在轨飞行的相对摄动加速度变化曲线.
由图2可以看出,摄动加速度是有界的,故推导式(9)前的假设以及k值的选取是合理的.图3给出了卫星编队构形的三维示意图,图4给出了相对位置和距离误差的变化曲线,图5给出了相对位置的放大图,图6给出了滑模面参数变化曲线,图7给出了控制加速度变化曲线.
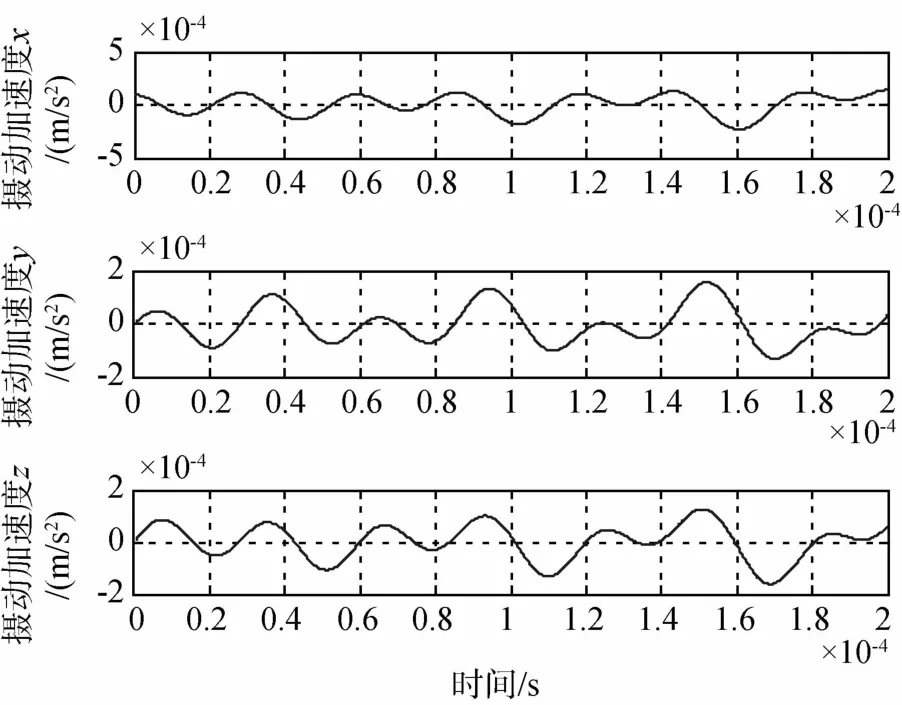
图2 相对摄动加速度变化曲线Fig.2 Curves of relative perturbation acceleration
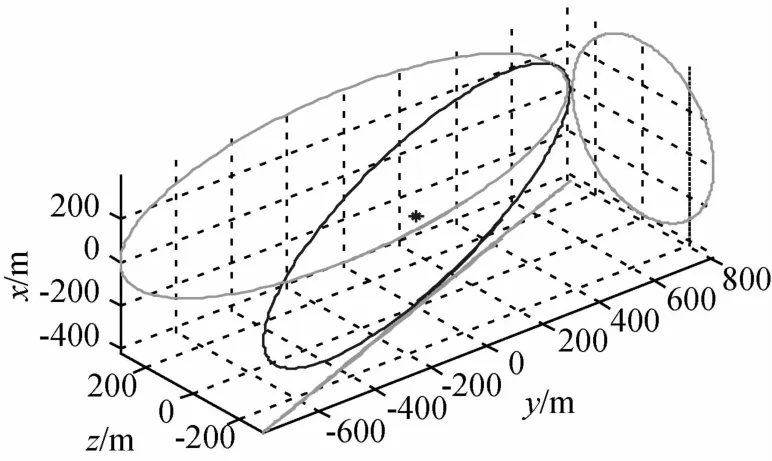
图3 卫星编队构形三维示意图Fig.3 Three-dimensional formation configuration
图3 给出了编队卫星的绕飞构形及其在Hill坐标系的投影.从图4和图5可以看出,在t=15888s时,编队卫星之间的相对距离与标称值偏差达到50m,控制器启动.在控制律(15)的作用下,相对位置和距离误差很快控制到零值附近,说明控制律(15)是有效的.x轴、y轴和z轴误差的收敛时间依次为292s、282s以及522s,收敛后的控制精度优于0.03m.
下面通过与控制器(16)和控制器(17)进行比较,说明控制律(15)的优越性,控制器(16)和控制器(17)的参数取值与控制律(15)的取值相同.图8~10给出了x轴,y轴和z轴的控制效果比较图.图11给出了3种控制器对应的y轴控制加速度比较图.
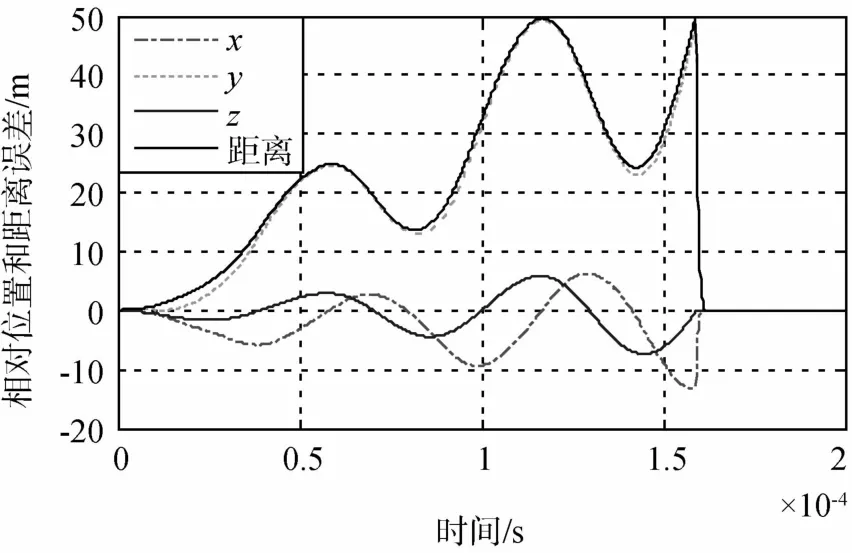
图4 相对位置和距离误差变化曲线Fig.4 Curves of relative position and distance errors
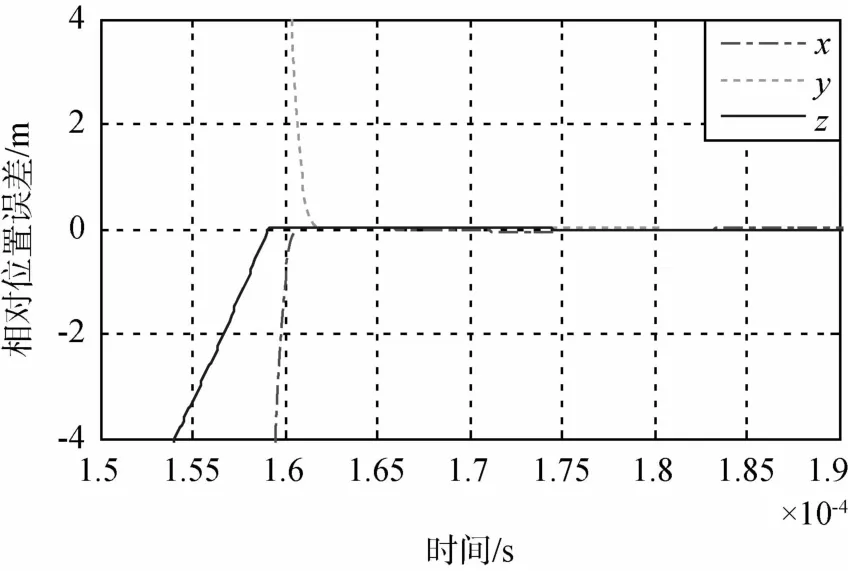
图5 相对位置误差的放大图Fig.5 Enlargement of relative position error
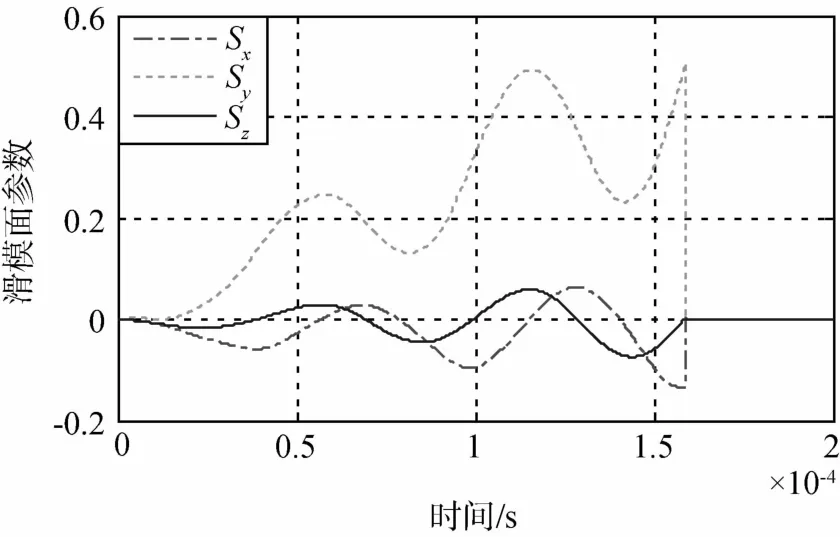
图6 滑模面参数变化曲线Fig.6 Curves of sliding mode manifold
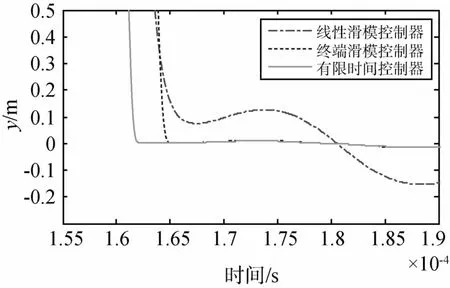
图9 y轴相对位置误差比较图Fig.9 Comparison of trajectory tracking error of y axis
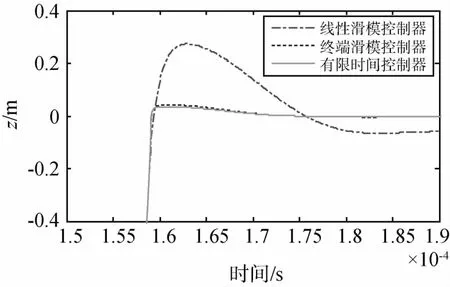
图10 z轴相对位置误差比较图Fig.10 Comparison of trajectory tracking error of z axis
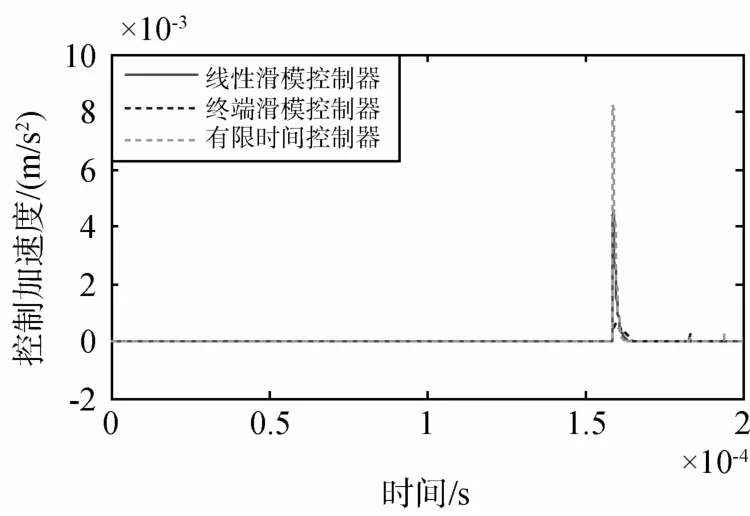
图11 三种控制器y轴控制加速度比较图Fig.11 Comparison of control accelerations of y axis for three controllers
由图8至图10分析可知,对于传统线性滑模控制器,x轴、y轴和z轴的状态误差收敛到0.15m的误差范围内需要的时间依次为1028s、3082s以及1082s.对于终端滑模控制器,x轴、y轴和z轴的状态误差收敛到0.03m的误差范围内需要的时间依次为422s、572s以及662s.可见,传统线性滑模控制器的收敛速度较慢,控制误差较大.终端滑模控制器在平衡点附近的收敛速度较快,控制误差较小.而本文提出的有限时间控制器不仅具有较高的控制精度,还具有更快的收敛速度.由于y轴沿航迹漂移引起的控制加速度较大,故图11以y轴控制加速度为例,给出了三种控制器的比较图.由图11分析可知,传统线性滑模控制器的总速度增量为1.177m/s,而有限时间控制器的总速度增量为1.766m/s.相比线性滑模控制而言,有限时间控制大大改善了控制效果,燃耗量仅增加了50%.
4 结 论
本文利用有限时间控制技术,设计了卫星编队构形维持控制律.该控制方法兼顾了传统线性滑模控制和终端滑模控制的优点,即使系统状态离平衡点较远,也具有较快的收敛速度,可以确保系统状态在有限时间内全局快速收敛.仿真结果表明,即使考虑多种摄动影响,有限时间控制方法不仅具有更快的收敛速度,还具有较高的控制精度,可以用在卫星编队构形快速重构和精密保持控制.
[1] Brown O,Eremenko P,Bille M.Fractionated space architectures:tracing the path to reality[C].Proceedings of the 23thAnnual AIAA/USU Conference on Small Satel-lites,Utah,USA,2009
[2] 张育林,曾国强,王兆魁,等.分布式卫星系统理论及应用[M].北京:科学出版社,2008:3-17 Zhang Y L,Zeng G Q,Wang Z K,et al.Theory and application of distributed satellite[M〛.Beijing:Science Press,2008:3-17
[3] Liu H,Li J F.Terminal slidingmode control for spacecraft formation flying[J].IEEE Transactions on Aerospace and Electronic Systems,2009,45(3):835-846
[4] 丁世宏,李世华.有限时间控制问题综述[J].控制与决策,2011,26(2):161-169 Ding SH,Li SH,A survey for finite-time control problems[J],Control and Decision,2011,26(2):161-169
[5] Ma G F,Lv Y Y,Hu Q L,et al.Terminal slidingmode attitude control for satellite[C].The 8thWorld Congress on Intelligent Control and Automation,Jinan,China, July 6-9,2010
[6] 丁世宏,李世华,罗生.基于连续有限时间控制技术的导引律设计[J].宇航学报,2011,32(4):727-733 Ding SH,Li SH,Luo S.Guidance law design based on continuous finite-time control technique[J].Journal of Astronautics,2011,32(4):727-733.
[7] Liu H,Li J F,Baoyin H X.Sliding mode control for low-thrust Earth-orbiting spacecraft formation maneuvering[J].Aerospace Science and Technology,2006 (10):636-643
[8] Yu SH,Yu X H,Shirinzadeh B,et al.Continuous finitetime control for robotic manipulators with terminal sliding mode[J].Automatica,2005,41(10):1957-1964
[9] 丁世宏,李世华.空间飞行器姿态的有限时间跟踪控制方法[J].航空学报,2007,28(3):628-633 Ding SH,Li SH.Finite time tracking control of spacecraft attitude[J].Acta Aeronautica et Astronautica Sinica,2007,28(3):628-633
[10] Wu SN,Sun X Y,Sun ZW,et al.Robust slidingmode control for spacecraft global fast-tracking manoeuvre[J]. The Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2011,225(G7):749-760.
[11] Wu S N,Radice G,Gao Y S,et al.Quaternion-based finite time control for spacecraft attitude tracking[J]. Acta Astronautica,2011,69:48-58
Finite-Tim e Control for Satellite Form ation Flight
HU Min1,ZENG Guoqiang2
(1.Academy of Equipment of people’s Liberation Army,Beijing 101416,China;2.College of Aerospace and Material Engineering,National University of Defense Technology,Changsha 410073,China)
A finite-time control scheme is proposed for satellites formation flight.Firstly,the nonlinear relative dynamics equation of formation flying satellites is established.Then,the sliding manifold with global fast convergence is designed,and a finite-time control technique is also presented,to guarantee global fast stability of the closed-loop system and fast convergence of the tracking errors.The theoretical proof of stability and convergence is given subsequently.Finally,formation keeping scenarios are carried out to validate the effectiveness and advantage of the finite-time controlmethod.Simulation results show that the developed finite-time control technique has faster convergence time and better control accuracy than traditional linear and terminal sliding mode controls.
satellite formation flight;finite-time control;sliding mode control;formation keeping
V448
A
1674-1579(2012)01-0023-06
胡 敏(1983-),男,博士研究生,研究方向为集群航天器动力学与控制;曾国强(1973-),男,教授,博士生导师,研究方向为分布式航天器动力学与控制,微纳卫星集群飞行.
*国家高技术研究发展计划资助项目(2010AA7026053).
2011-07-28
DO I:10.3969/j.issn.1674-1579.2012.01.004
