基于T－S模糊神经网络的覆冰厚度预测模型

2012-09-04刘军李安均赵丽萍

湖南电力 2012年3期

刘军，李安均，赵丽萍

(1.湖南省电力公司娄底电业局，湖南娄底417000;2.长沙理工大学，湖南长沙 410114)

近年来，中国大部分地区输电线路时常遭受覆冰灾害，极端覆冰灾害造成输电线路覆冰过荷载，严重威胁电网的安全可靠运行，造成巨大的经济损失〔1-3〕。为此，有必要对覆冰厚度进行准确预测，从而制定有效的防冰策略，保障输电线路的安全可靠运行。考虑覆冰厚度受风速、环境温度、降雨量等气象条件的影响，而众多气象条件之间相互影响且具有各种不确定性，其幅值波动常呈现较强的非线性特性。同时，气候环境与各气象条件间的相关性错综复杂，相互之间的主导性难以确定，数量关系也难进行定量分析。

目前覆冰厚度预测模型的研究主要集中在热动力学模型，然而热动力学参数太过复杂很难确定，常导致模型无法求解，从而难以直接应用于电力覆冰厚度预测〔4-5〕。与热动力学模型相比，神经网络模型属于大规模非线性动态网络结构，适用于非线性系统的建模，且具有并行处理的能力，自适应和学习能力强，对非线性系统的拟合预测具有良好效果〔6〕。然而，神经网络只能将初始权值取为零或随机数，因而使网络的训练时间变长或得到不合理的局部极值，而Takagi-Sugeno(简称T－S)模糊模型能用比较少的规则数来描述未知的系统模型，其结论部分通过线性模型来表述，即将一个非线性系统划分为多个线性系统的模型，结论参数的辨识快速、简单、有效。同时，通过神经网络对T－S模型的结构辨识和参数辨识能够自主地对模糊规则进行初始化，且能自适应调整前提隶属度参数和结论参数，通过对输入量的模糊聚类，有效地处理了误差反传算法陷人局部极小点的问题，并对解决T－S模型时随着辨识系统复杂度增加，其规则数目变多的问题提供了有效的帮助〔7〕。

因此，本文提出了一种将时间序列方法和T－S模糊神经模型相结合的覆冰厚度预测模型。

1 预测模型的建立

1.1 时间序列模型

时间序列分析主要指:预测一个事物的发展趋势，用过去行为来预测未来的变化趋势，即用该事物的历史数据来揭示该事物随时间变化的规律，将这种趋势延伸到未来，从而对该事物的未来作出有效预测，其原理是将一个事物非平稳序列转化为平稳序列〔8-9〕。本文分别对影响覆冰厚度的气象因子等数据建立自回归模型AR(n)，即:

式中 φi(i=1，2，…，n)为自回归参数;{at}为白噪声序列且at∈N(0，σ2a)。由于原始气象因子数据值可能过大或过小，为保证计算的精度、减小误差、避免溢出，可对数据进行标准化处理。记 {x'(t)}为各原始气象因子数据，对 {x'(t)}中各气象因子数据进行如下标准化处理:

式中 μx为 {x'(t)}的均值估计，其数学表达式为:

式中 σx为 {x'(t)}的方差估计，其数学表达形式为:

式 (3)， (4)中，n为各气象因子数据的个数。由式 (2)所得的时间序列 {x(t)}通过式 (1)进行建模，得预测的时间序列如下:

1.2 T－S 模糊神经网络

设输入变量为 x=〔x1，x2，…，xn〕T，且每个输入分量xi均为模糊语言变量。模糊语言变量值的集合为:

式中 Ami是xi的第m个语言变量值，它是定义在xi范围内的一个模糊集合。

因此，T－S模型的模糊规则形式表示为:

若输入变量采用单点模糊集合的模糊化方法，则对于给定的输入量，可求得其对应的每条规则的适应度为:

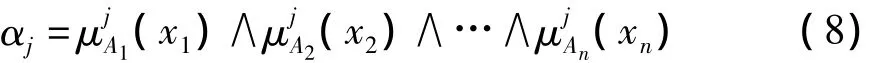
式中 μj为输入x对应的隶属度函数。A1i

模糊系统的输出值为每条规则输出值的加权平均值，即:

由上述T－S模型，可以画出如图1所示的TS模糊神经网络结构图。该网络分为前件网络和后件网络，前件网络主要用来匹配模糊规则的前件参数，后件网络主要用来产生模糊规则的后件参数。

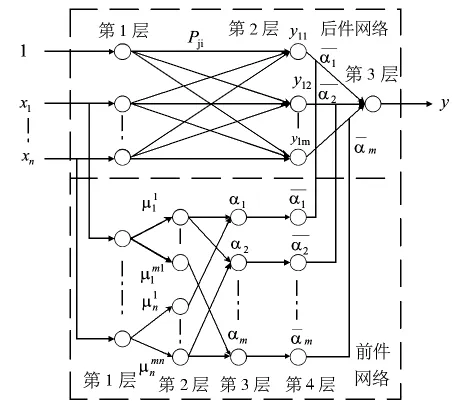
图1 T－S模糊神经网络结构图

T－S模型的前件网络有4层。第1层作为输入层，它的每个节点直接与各输入分向量xi相连接，起到将各输入量传送到下一层的作用。

第2层的作用是计算出各输入分量的隶属度函数μji，每个节点代表一个语言变量值，其中:

若隶属函数采用高斯函数表示的铃形函数，则

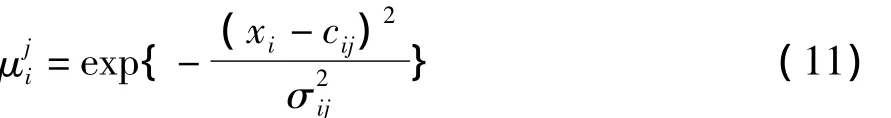
第3层的每个节点分别代表1条模糊规则，它主要是匹配模糊规则的前件参数，计算每条规则的适应度，即:

该层的结点总数N3=m。对于给定的输入量，只有在输入点附近，语言变量值才能取得较大的隶属度值，远离输入点的语言变量值的隶属度将会很小。因此，在Aj中只有少量节点会有较大输出，这一点很类似于局部逼近网络。

第4层的作用是实现归一化计算，其节点数与第3层相同，即:

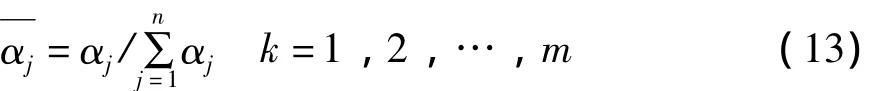
后件网络是由r个相同结构的并列子网络构成的，每个子网将产生一个输出值。子网络的第1层为输入层，其中第0个节点的输入为1，是为了提供模糊规则后件中的常数项。

子网络的第2层有m个节点，每个节点分别代表1条规则，它主要是计算出每1条规则的后件，即:

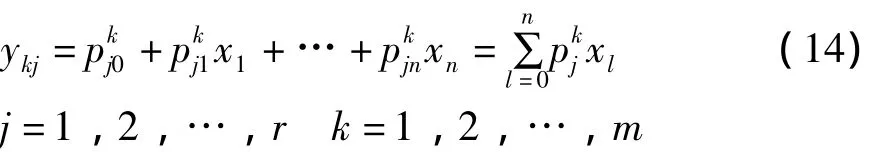
式中 x0=1。

子网络的第3层是系统的输出层，即:

若各输入分量的模糊分割数已知，则T－S模糊神经网络的待定参数为需要学习的参数，主要是后件网络的连接权pkij、前件网络中第2层各节点隶属度中心值cij及宽度σij。取误差函数为:

式中 ydi和yi分别表示期望输出和实际输出。以下给出连接权pky的学习算法:

固定参数Pkij可得

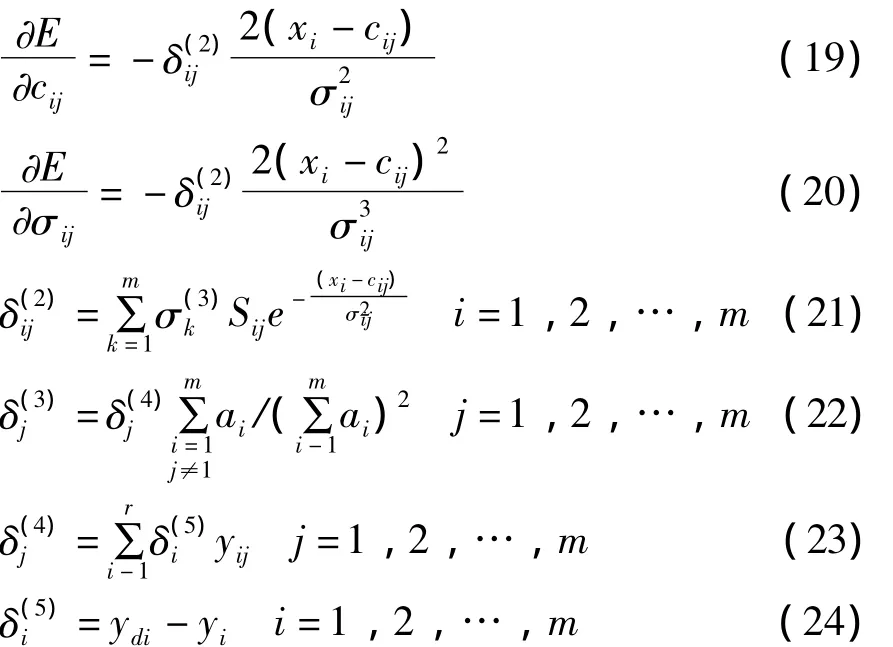
式中 β＞0为学习率。

2 算例分析

由于覆冰厚度R受风速V、环境温度T、降雨量P、覆冰时间N等因素的影响。根据2008年郴州电网220 kV东城线路连续10天的部分覆冰数据(表1)建模，由于风速V、环境温度T、降雨量P等气象因子具有明显的波动性和随机性，本文先用AR(n)模型对这些气象因子进行预测。将这些气象因子的预测数据作为训练样本，然后根据图1所示的模糊神经网络对其进行训练，调整网络参数。

表1 覆冰数据

将输入量均分为5个模糊等级，它们分别对应从N到P的5个模糊语言，即mi=5。隶属度函数的形状为铃形分布，需要调整的是后件网络参数的连接权pkij、前件网络参数的隶属度中心值cij和宽度σij。为了便于比较，本文采用3组不同的输入变量来比较本文提出的模型的精确度。其输入形式如下:①〔V(t)，T(t)，P(t)，y(t)〕;②〔V(t)，V(t－1)，T(t)，T(t－1)，P(t)，P(t－1)，y(t)，y(t － 1)〕;③ 〔V(t)，V(t－1)，V(t－2)，T(t)，T(t－1)，T(t－2)，P(t)，P(t－1)，P(t－2)，y(t)，y(t－1)，y(t－2)〕(其中，V(t)为在t时刻的风速;T(t)为在t时刻的环境温度，P(t)为在t时刻的降雨量，y(t)为在t时刻的覆冰厚度)。第1组输入量表明，在预测覆冰厚度时，只需考虑预测点这一时间点，即t时的气象数据;第2组输入量表明，在预测覆冰厚度时，需考虑预测点这一时间点和前一个时间点，即t，t－1时的气象数据;第3组输入量表明，在预测覆冰厚度时，需考虑预测点这一时间点和前2个时间点，即t，t－1，t－2时的气象数据。

在第1—3种情况下，覆冰厚度的预测值和实际值的比较分别如图2(a)—图2(c)。