两步单参数法研究支承偏心对弯箱梁桥的影响
2012-09-04宋国华王东炜
宋国华,罗 玲,霍 达,王东炜
(1.郑州大学土木工程学院,河南郑州 450001;2.北京市市政工程设计研究总院,北京 100045;3.北京工业大学建筑工程学院,北京 100124)
两步单参数法研究支承偏心对弯箱梁桥的影响
宋国华1,罗 玲2,3,霍 达3,王东炜1
(1.郑州大学土木工程学院,河南郑州 450001;2.北京市市政工程设计研究总院,北京 100045;3.北京工业大学建筑工程学院,北京 100124)
为了研究支承偏心对弯箱梁桥的影响,以桥长、圆心角和支承偏心距为参数建立了270个两等跨连续弯箱梁桥模型,采用两步单参数拟合法进行数据处理,拟合出极限状态下的截面配筋内力、单位位移及支承反力与圆心角、桥长和支承偏心距的显示函数关系。得到各种结构反应受该三参数影响的变化趋势及程度大小。认为通过统计分析和数值模拟的方法拟合出结构反应与圆心角、桥长及支座偏心距间的显示函数关系,方法可行,结果可靠。可知受偏心距影响的结构反应与偏心距为线性关系,可以通过两个指标来定性表征结构反应随偏心距增大而变化的情况以及变化程度的大小。
弯箱梁桥 支承偏心 两步单参数法 圆心角
在弯梁桥结构中,为了改善梁内扭矩的分布和桥墩的受力状态,往往采用偏心设置的支座,即支座中线不通过梁的中线[1-2]。这种情况多用于具有独柱墩的连续弯梁桥中。
在点铰支承处给以一定的预偏心,可以达到人为调整结构扭矩分布形式的目的,使连续弯梁沿梁长方向的扭矩峰值得到控制,从而使结构所承受的扭矩分布趋于合理。点铰的预偏心实际上是在点铰处人为施加一反向的集中扭矩,以达到调整连续弯梁的扭矩峰值的目的,这和设置抗扭支座的目的是一致的[1,3-4]。
支座径向外移,不但可以改善端部支座内、外侧支反力的分配,使端部内、外侧支座反力趋于均衡,避免不利荷载作用下支座脱空;还能使端部支座的反扭矩随偏心距的增大呈线性减小。支座偏心对剪力影响很小,特别是活载作用下,几乎没有影响。偏心距变化,边跨恒载扭矩图近似地发生“平移”和微小的“转动”,最大扭矩和最小扭矩同时增大或同时减小,当偏心距选择适当时,可使最大扭矩和最小扭矩的绝对值趋于相等[2,5]。
总之,弯梁桥中间点铰支承设置预偏心,使静载扭矩沿梁长方向趋于均匀,同时使抗扭支座的支点反力更趋均匀,增加了全桥的侧向稳定性,经济效益显著,美观上收到良好效果。
本文主要研究桥长L、圆心角φ和支承偏心距e对两等跨连续弯箱梁桥的结构反应的影响。提出以梁格系法为理论基础编制的“斜弯坡及异形空间分析软件系统3D-BSA”为结构计算分析工具,以EXCEL为数据处理工具,用两步单参数法建立变截面两跨弯箱梁桥受力性能与圆心角及桥长间的显示函数关系。
1 模型建立
研究参数有圆心角φ、桥长L以及支承偏心距e,它们的取值范围如下:
1)φ 值为 30°,60°,90°,120°,150°;
2)L 值为 50,70,80,100,130,150 m;
3)e值为 0,0.2,0.4,0.6,0.8,1.0,1.5,2.0,2.5 m。
根据参数的数量和取值,共建立了5×6×9=270个模型,模型的建立步骤同文献[3],只是在建立支承单元时根据偏心距e向桥外方向移动一定距离而已。图1示出了圆心角φ=60°,桥长L=100 m,偏心距e=1.0 m的模型的支承偏心情况。

图1 支承偏心1.0 m
模型计算包括四部分:数据处理,施工计算,活载计算及荷载组合。因由软件3D-BSA计算,故不再赘述。
2 两步单参数拟合法数据处理
2.1 所关心的结构反应
所关心的结构反应包括分别在正常使用极限状态和承载能力极限状态下控制截面的内力,和局部坐标系下施工阶段4自重作用下的位移,以及组合1和组合2工况下支承单元的反力。因为,上述内力为截面的配筋内力,上述位移最能反映支承偏心对结构的影响情况,而支承反力反映了支承本身随偏心距的变化情况。
2.2 拟合过程
两步单参数法数据处理是先拟合结构反应与偏心距e间的关系曲线,再拟合其表达式的各个系数和常数与桥长L或圆心角φ间的关系曲线。由于各变量间的相关关系,一般较难进一步拟合出与第三个变量的关系,所以这种方法只能用于拟合在桥长L(或圆心角φ)一定时结构反应与偏心距e及圆心角φ(或桥长L)的关系曲线,而且通常可靠度较高。
在圆心角φ一定时,该法拟合的结果具有以下形式
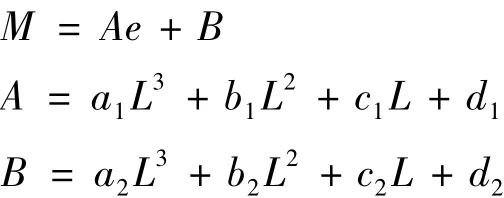
式中,M代表所关心的任意一种结构反应;A,B为系数,均为 L的多项式;带下标的 a,b,c,d均为系数。
由上可知,结构反应M和偏心距e均是线性关系。如果知道A的正负,就可以知道M随偏心距e的增大而增大(或减小)的情况。但是增大(或减小)的程度会随着L的变化而变化。这里用ΔL来表示这种变化程度,ΔL=dA/dL=3a1L2+2b1L+c1,即A关于L的曲线的斜率。
当ΔL>0时,表示M随e的变化程度随着L的增大而增大;当ΔL<0时,表示M随e的变化程度随着L的增大而减小;当ΔL=0时,表示M随e的变化程度不受L影响。
另外,上式中B仅为L的函数,当e=0时,B与L的关系即为M与L的关系,将在其它文章中讨论。当然,以上讨论中L和φ可互换。
用A的正负及ΔL及Δφ的正负来表示所关心的结构反应随e的变化情况及变化程度的大小,见表1。
2.3 拟合结论
1)内力 Qz,Mz,My;支承反力 Rx;位移 w,θy均只与桥长L和圆心角φ有关,设计时可不考虑支承偏心的影响。

表1 结构反应随偏心距e变化的指标
2)内力Qy及支承反力Ry(1),Tz(2)可以用多项式表达,其参变量为桥长L、圆心角φ和偏心距e。
3)桥梁在水平面内的反应,如Mz,Ry(2)和Tz(1)及除v外的所有位移用经验公式计算误差较大。
4)各项反应Nx及 θz值都很小,设计时可忽略不计。
3 结语
1)通过统计分析和数值模拟的方法拟合出两等跨偏心支承连续弯箱梁桥结构反应与圆心角、桥长及支座偏心距间的显示函数关系,方法可行,结果可靠。
2)通过先拟合偏心距,再拟合桥长(或圆心角)的两步单参数拟合法,可知受偏心距影响的结构反应与偏心距为线性关系,可以通过两个指标来定性表征结构反应随偏心距增大而变化的情况以及变化程度的大小。
[1]单德山,李乔,蔡乐军.高速铁路曲线梁桥的合理结构形式初探[J].国外桥梁,2000(3):59-63.
[2]韩皓,李彬,曹劲松.支座预偏心对曲线箱梁桥受力影响研究[J].华东公路,1999(4):32-35.
[3]宋国华,罗玲,王东炜.偏心支承对120°圆心角双跨弯箱梁桥的影响[J].桥梁建设,2005(4):44-47.
U448.21;U448.42
A
1003-1995(2012)06-0004-02
2011-09-22;
2012-03-12
国家自然科学基金资助(50978232);河南省教育厅自然科学研究计划项目(2009A560014)
宋国华(1973— ),女,河南滑县人,副教授,博士。
(责任审编 白敏华)
