纯电动汽车动力总成悬置系统的优化*

徐中明，李 晓，刘和平

(重庆大学，1.机械传动国家重点实验室;2.机械工程学院;3.输配电装备及系统安全与新技术国家重点实验室，重庆 400030)

前言

动力总成悬置是指利用较柔软的连接元件将动力总成与车架相连接，从而衰减二者之间的振动传递，起到隔振、支承和限位的作用。动力总成悬置系统的隔振性能直接影响到整车的NVH性能。目前，国内外对发动机动力总成悬置系统的研究已较深入，论文成果也较多。常采用的研究方法主要有转矩轴解耦［1］和能量解耦［2］等。文献［3］～ 文献［5］中在这方面做了比较深入的研究，分析了悬置参数对悬置系统的固有频率、解耦鲁棒性和总成质心位移与支承处动反力幅频特性的影响。

对于纯电动汽车动力总成悬置系统的研究工作主要集中在动力总成固有特性的分析和优化匹配上，没有结合电机驱动的特点进行起步、制动和其它工况的瞬态分析［6］。电动机与发动机的特性有很大不同，传统的分析方法可以借鉴，但在研究纯电动汽车动力总成悬置系统的隔振问题时必须考虑电动机的特点。

本文中采用ADAMS软件对电动汽车的动力总成悬置系统进行建模。根据电动汽车在实际运行中出现的振动问题，结合电机的驱动特性对电动汽车的加速和制动两种工况进行仿真分析，并以能量解耦为目标对其进行优化，以期为解决电动汽车动力总成悬置系统的振动问题提供一种有效途径。

1 动力总成悬置系统动力学建模

该动力总成由三相异步感应电机、减速器和差速器组成，其中差速器集成在减速器内。动力总成和悬置元件一起组成动力总成的悬置系统，其固有频率通常在30Hz以下，比动力总成自身的自由模态频率低得多。因此在研究动力总成悬置系统的隔振特性时将动力总成简化为6自由度的刚体模型，将橡胶悬置元件简化为3向正交的弹簧阻尼模型。电动车动力总成如图1所示。其中①②③分别表示3个橡胶悬置元件的安装位置。

坐标系原点取在该动力总成的质心处，X轴平行于水平面并指向汽车前进方向，Z轴垂直向上，Y轴平行于电机转子轴线，方向根据右手定则确定。定义动力总成的振动分别为在X、Y、Z轴上的平动x、y、z和绕 X、Y、Z 的转动 α、β、γ，则动力总成的广义坐标可表示为

根据振动理论建立动力总成悬置系统的振动微分方程为

式中:［M］为质量矩阵;［C］为阻尼矩阵;［K］为刚度矩阵;{Q(t)}为广义坐标向量;{F(t)}为广义力向量。

在求解动力总成悬置系统的固有频率时不考虑阻尼的影响，则其无阻尼自由振动微分方程为

2 悬置系统固有特性和耦合特性分析

固有频率是动力总成悬置系统的重要特性之一，通过分析悬置系统的固有频率可以判断其是否满足悬置系统的隔振性能要求。悬置系统的固有频率可通过式(3)变换后得出，即

通常动力总成悬置系统6个自由度方向上的振动是相互耦合的，一个方向上的激励会引起多个方向上的振动。这一般会使系统的振幅加大，振动频带加宽。

利用ADAMS/Vibration模块计算该动力总成悬置系统的各阶固有频率和模态能量解耦率，其结果如表1所示。

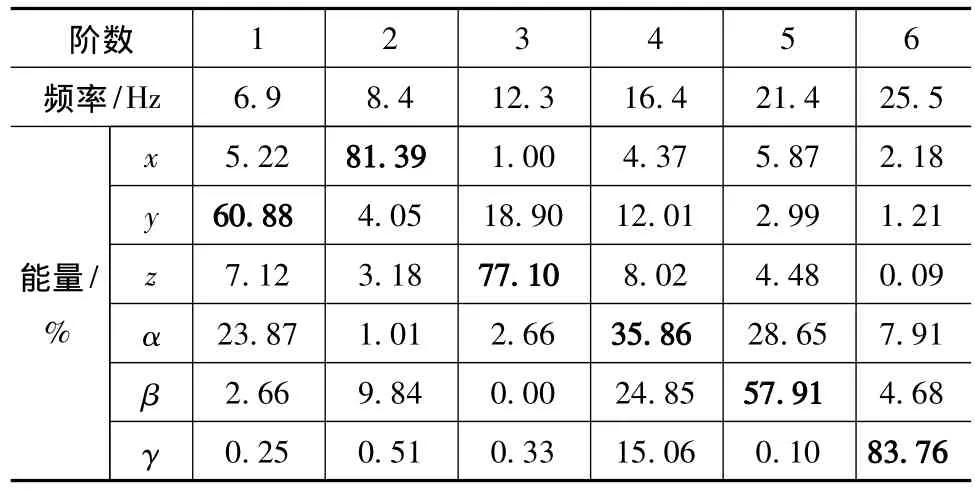
表1 动力总成悬置系统各阶固有频率和振动能量

电动汽车车身的频率在2Hz左右，轮胎频率在10Hz左右，由表1可知，该动力总成悬置系统的固有频率在6～30Hz之间，垂向频率12.3Hz。从频率来看和固有频率不很接近。从其能量分布百分比上看，各方向的解耦率都不高，最高的解耦率(第2阶的x向和第6阶的γ向)也只有81.39%和83.76%，最低的解耦率仅35.86%，说明该悬置系统的耦合非常严重，设计很不合理。

3 动力总成悬置系统瞬态响应分析

电动机与发动机的动力特性有很大不同。电动机在转速为零时也能输出很大的转矩，且响应速度很快，能够在极短时间里使输出转矩发生很大变化。运行中发现电动汽车在急加速和紧急制动工况下其悬置系统的振动非常严重。

利用ADAMS/View对电动汽车的加速和减速工况进行仿真分析。在10s的时间里同时计算电动汽车在加速和减速两种工况下的瞬态响应。其中0～5s这一时间段电动汽车以最大驱动力矩原地起步加速，5～10s这一时间段电动汽车通过控制器以能量回馈的方式进行制动。电机的最大驱动力矩为120N·m，制动力矩为80N·m，电机响应时间取1ms，同时考虑动力总成所受重力和惯性力的影响。惯性力通过样车整车结构参数和驱动(制动)条件计算加(减)速度来确定。仿真中忽略电机转矩波动的影响，转矩的加载曲线如图2所示，动力总成惯性力的加载曲线如图3所示。

仿真结果如图4～图8所示。

由图4～图8可见，在0～2s的时间段，即电动汽车在驱动时动力总成悬置系统主要的瞬态响应阶段，曲线振动较大，之后振动趋于稳定。制动时系统从稳态阶段进入瞬态阶段，在系统主要瞬态阶段的5～7s，振动也较大，之后又逐渐趋于稳定。这个过程符合实际中汽车在起步和制动时悬置系统从稳态进入瞬态，之后又恢复到稳态的状况，说明用10s时间同时仿真计算电动汽车的起步和制动过程是可行的。

从图4～图6可以看出，驱动工况时动力总成悬置系统的质心Z向位移较大，幅值接近3.5mm，质心Z向加速度也较大;制动时质心Y向角加速度较大。这主要是由于电动机动力总成自身激励的特点使动力总成悬置系统在Z向的垂直振动和绕Y轴的俯仰振动比较严重，另外路面激励也是一部分原因。从能量耦合的程度也可看出，第3阶模态的Z向能量解耦率只有77.10%，第5阶模态的β向能量解耦率只有57.91%，耦合相当严重。

由图7和图8可见，橡胶悬置元件的Z向受力和变形比较大。其中悬置2的值最大，最大力为876N，最大为位移4.9mm。制动时力和位移的变化范围也较大。这样不仅会产生运动干涉，还容易使橡胶元件发生疲劳破坏。

4 悬置系统优化

4.1 优化目标

动力总成悬置系统的优化可从多个角度来选择优化的目标函数。如以系统固有频率合理匹配为目标、以能量解耦为目标、以振动传递率最小或支承处动反力最小为目标和以人体垂向振动加速度均方根值最小为目标等，或综合以上多个设计指标进行多目标优化［7］。

理论上讲当悬置系统的弹性中心与动力总成的质心重合时，动力总成悬置系统在各个方向上的振动完全解耦。但实际上由于受到悬置元件本身性能和整车布置空间的限制，一般难以实现。只能通过合理设计悬置参数以期使悬置系统各个自由度方向上的解耦达到相对最优。本文中以能量解耦为目标对该动力总成悬置系统进行优化。

4.2 设计变量

从式(2)动力总成悬置系统的振动微分方程可以看出，影响悬置系统隔振性能的量有质量矩阵、刚度矩阵和阻尼矩阵，它们涉及动力总成的质量与惯量参数、刚度和阻尼参数以及悬置元件的安装位置和安装角度等。在对动力总成悬置系统进行优化时一般不对系统的质量和惯量参数进行修改;悬置元件的阻尼对系统的振动影响很大，主要作用是降低系统的共振峰值，文中采用固定阻尼比，不将阻尼作为设计变量;悬置元件的安装位置和安装角度由于受到安装空间的限制，不可能有大的改变，因此综合考虑之后，以3个橡胶元件共9个刚度参数作为设计变量进行解耦优化。

4.3 约束条件

为防止运动干涉，该电动汽车动力总成悬置系统的质心位移要小于5mm。悬置系统的1阶固有频率要高于悬挂质量部分的固有频率(一般为1～2Hz)和座椅的固有频率(一般为3～4Hz)，以免发生共振。因此根据隔振理论，该动力总成悬置系统的1阶固有频率应大于。考虑到该电动汽车布置空间的限制，将悬置元件的坐标位置调整为表2所示的值，悬置元件的安装角度不变。

表2 悬置元件弹性中心坐标 mm

4.4 优化结果分析

运用ADAMS/Insight模块采用3阶响应面试验设计对该电动汽车的动力总成悬置系统进行优化。首先在ADAMS/Vibration模块下建立悬置系统能量解耦的6个设计目标，再将橡胶元件的9个刚度参数设为设计变量，然后导入Insight模块进行计算，得到橡胶元件的刚度参数见表3。优化后悬置系统的固有频率和能量分布百分比如表4所示。

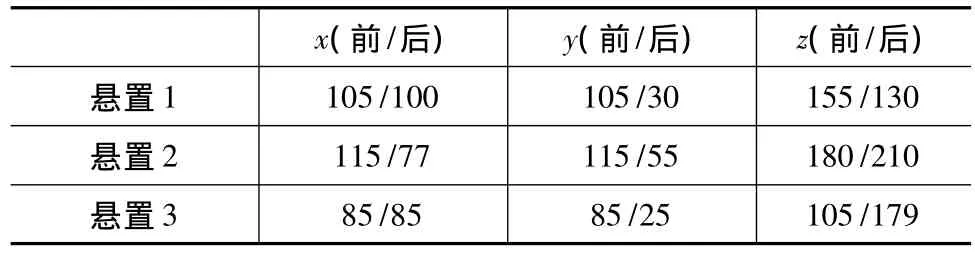
表3 优化前/后橡胶悬置元件的刚度 N/mm

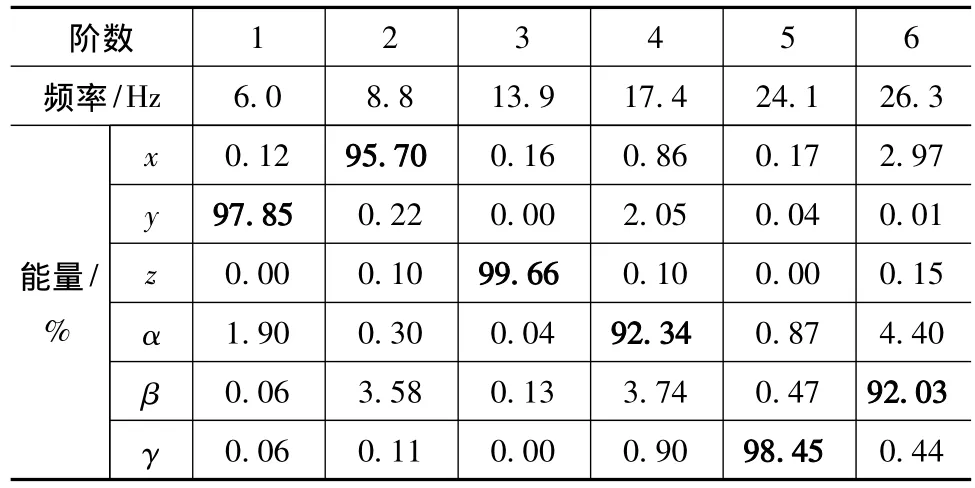
表4 优化后悬置系统各阶固有频率和振动能量

从表4和表1的对比可知，优化前后固有频率值变化并不大，但能量解耦情况却有显著改善，6阶模态的解耦率都达到了90%以上。优化后的瞬态响应结果如图9～图16所示。

从计算结果可以看出，经解耦优化后，在电动汽车起步和制动两种工况下动力总成悬置系统的瞬态响应情况得到了很大改善。下面从动力总成悬置系统Z向的瞬态响应情况加以说明。

由图9～图10可知，优化后动力总成悬置系统的质心Z向振动位移峰值由3.5mm降低到2mm，振动加速度峰值由10050mm/s2降低到8300mm/s2左右，起步和制动时的振动值都明显降低，并且由于振动能量降低使振动的衰减加快。

由图11～图13可知，优化后3个橡胶悬置元件的Z向受力情况明显改善，力的峰值和振动稳定后的值都明显降低，振动也衰减得很快。

由图14～图16可知，优化后3个橡胶悬置元件的Z向位移变形明显减小，振动衰减得很快。特别是第3个橡胶悬置元件的变形量减小得最多，由4mm降到2mm左右。

5 结论

采用动力学仿真分析软件ADAMS的View、Vibration和Insight模块对纯电动汽车的动力总成悬置系统进行了仿真分析和能量解耦优化，优化后的能量解耦率很高，取得了很好的效果。通过对电动汽车急加速和紧急制动两种工况进行瞬态响应计算获得了该电动汽车的动力总成悬置系统的瞬态振动特性，经解耦优化后，动力总成悬置系统的瞬态响应特性得到了很大改善。这说明通过能量解耦的方法能很好地解决动力总成悬置系统的振动问题，为电动汽车动力总成悬置系统的设计提供依据。

［1］Jeong T，Singh R.Analytical Methods of Decoupling the Automo-tive Torque Roll Axis［J］.Journal of Sound and Vibration，2000，234(1):85-114.

［2］江合连.混合动力轿车动力总成悬置系统隔振与优化研究［D］.长春:吉林大学，2008.

［3］吕振华，范让林.动力总成—悬置系统振动解耦设计方法［J］.机械工程学报，2005，41(4):49-54.

［4］上官文斌，黄天平，等.汽车动力总成悬置系统振动控制设计计算方法研究［J］.振动工程学报，2007，20(6):577-583.

［5］吴杰，上官文斌，等.动力总成悬置系统解耦布置的鲁棒性分析［J］.振动与冲击，2009，28(9):15-20.

［6］王珣，张立军，王建.燃料电池轿车电动动力总成悬置系统动态特性分析［J］.汽车技术，2009(2):29-32.

［7］宋才礼.动力总成悬置系统隔振性能研究［D］.镇江:江苏大学，2009.

［8］余卓平，王建，等.燃料电池轿车动力总成悬置系统的优化设计［J］.机械设计，2009，26(7):50-53.

［9］Yu Yunhe，Naganathan Nagi G，Dukkipati Rao V.A Literature Review of Automotive Vehicle Engine Mounting Systems［J］.Mechanism and Machine Theory，2001，36:123-142.