爱因斯坦的“光子箱”悖论和塔尔斯基型解悖

韩锋

(河池学院物理与电子工程系，广西宜州546300)

爱因斯坦的“光子箱”悖论和塔尔斯基型解悖

韩锋

(河池学院物理与电子工程系，广西宜州546300)

“光子箱悖论”是爱因斯坦—玻尔论战中的一个关节点。通过分析爱因斯坦的“光子箱”悖论及其解悖过程，揭示这类悖论解悖方法对我们的启示:它们都是通过塔尔斯基所提出的分层方法得到解决的。深入理解这种塔尔斯基分层型解悖，把它发展成为普适性的解悖模式，是很有意义的。

爱因斯坦;尼耳斯·玻尔;光子箱;塔尔斯基型解悖

尼耳斯·玻尔是与爱因斯坦齐名的物理学家，它与爱因斯坦的世纪论战更是脍炙人口，对推动近代物理学迅速成熟具有重要意义。1962年的哥本哈根，77岁的尼耳斯·玻尔仍然不能忘怀，在32年前1930年的第六次索尔维会议上爱因斯坦为反驳量子理论而提出的“光子箱模型”(又称“光子盒”模型)。这个理想化模型成为确立量子理论的决定性关键论据而永载史册。无论是爱因斯坦还是玻尔，都非常珍视提出这个模型时的智慧和解决它时的巧思，以致在玻尔去世时，他的工作室黑板上最后留下的，就是这个“光子箱模型”的草图(如图1所示)。爱因斯坦的质疑，极大地推动了量子物理学的发展，玻尔也一定不止一次地从他的这位伟大对手那里，寻求过灵感的光芒。虽然爱因斯坦已经先他7年离世，他的那个著名的悖论也早已得到解决。从那时起到现在又过去了80多年，更多的形形色色的悖论也都逐渐得到了解决，可是当年这个悖论所带给我们的启示，仍然需要深入剖析，并从中提升我们的智慧。

1 “光子箱悖论”提出的背景

人们公认，量子力学的物理内容是没有问题的，它的计算结果也和实验符合得很好。可是，如何理解和解释量子现象中的那些“怪异”行为，却一直是大家争论不休的问题。这也就是关于量子力学的物理诠释问题。以爱因斯坦为首，包括薛定谔、德布罗意等一批物理学家，从一开始就很不喜欢像“测不准关系”这样一些量子力学的基本原理(尽管他们也认同从中得到的、与实验符合得很好的计算结果)，总想找出有力的论据来推翻它。而以玻尔为首的，包括海森堡、玻恩等一批物理学家，则认为不但量子力学的物理内容是正确的，而且包括“测不准关系”以及由它引申出来的“互补原理”等物理诠释也是正确的。他们为此持续争论了30多年，直到1955年爱因斯坦去世。7年以后玻尔也去世了，而其余波则至今未平。对于这场著名的爱因斯坦—玻尔论战，著名物理学家J.A.惠勒有过一段很好的描述:“近几百年来很难再找到其他的先例能和这场论战相比拟，它发生在如此伟大的两个人物之间，经历了如此长久的时间，涉及如此深奥的问题，而却又是在如此真挚的友谊之中。”［1］2

图1 “光子箱模型”草图

以玻尔为代表的对量子力学的那套解释被称为哥本哈根诠释，为了驳倒这个解释，在1927年的第五届索尔维会议上，爱因斯坦打算通过电子的单缝衍射和双缝干涉的理想实验，从坐标和动量的测量方面来否定测不准关系，进而否定玻尔的那个“在主体和客体之间不可能保持任何明确分界线”的认识论观点［2］。结果被玻尔他们在经过仔细地分析以后，却从那个理想实验中得出了测不准关系，爱因斯坦一派的首战没有成功。

在1930年的第六届索尔维会议上，爱因斯坦又换了一个角度，试图从能量和时间的测量方面来否定测不准关系。这就是本文所要分析的“光子箱”理想实验。

顺便指出，索尔维(E.Ernest Solvay，1838－1922)是一个和诺贝尔一样的著名实业家，诺贝尔设立了以他的名字命名的科学奖金，索尔维则以其万贯家财设立了以他的名字命名的科学会议。这个会议每三年召开一次，讨论当时物理学和化学发展中尚待解决的重大问题。

2 爱因斯坦的挑战——“光子箱悖论”

1930年秋，第六届索尔维会议在布鲁塞尔召开，早有准备的爱因斯坦在会上向玻尔提出了一个著名的思想实验——“光子箱”，这使爱因斯坦与玻尔的这场论战掀起了一个新的高潮。

这个理想实验的装置如图2所示。

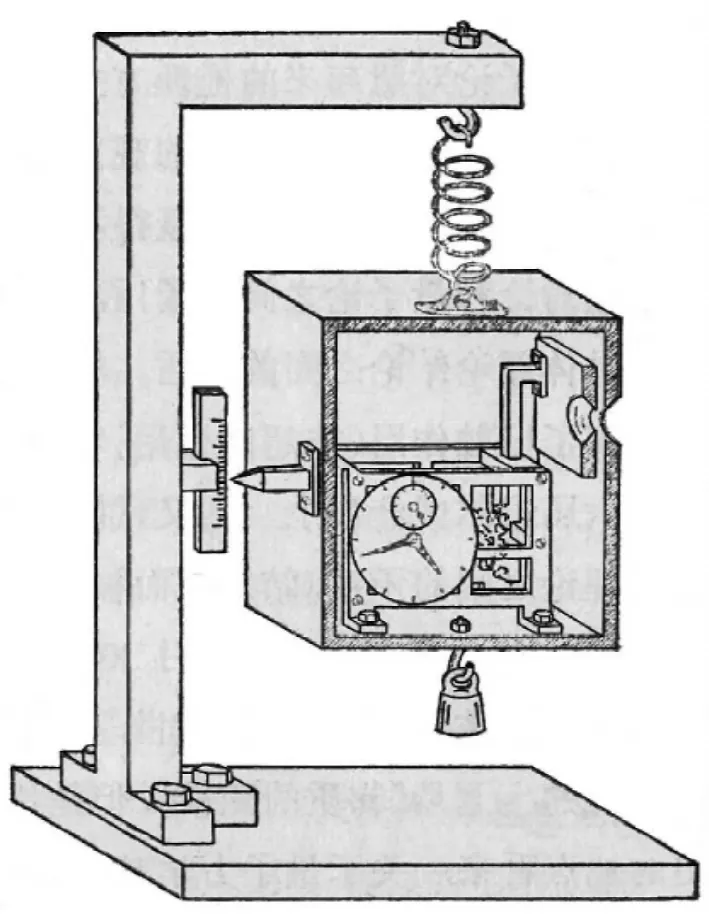
图2 “光子箱”理想实验装置图

他设想了一个具有理想反射壁的箱子，里面充满了辐射。箱子上有一快门，可以用箱内的时钟控制它的启闭。快门启闭的时间可以任意的短，每次开启只释放出一个光子。只要准确测出光子释放前后整个箱子质量的变化，就可以根据相对论质能关系式E=mc2，精确地测定光子的能量变化ΔE。因为质量的测量是在开窗之前与开窗之后，与Δt无关，这样测定光子的能量就可以超出Δt·ΔE≥给出的测量精度，就总有可能使Δt·ΔE＜，于是证明了测不准关系不成立。

这个“光子箱”的具体装置是这样的:设有一个用弹簧秤挂在固定底座上的不透明的箱子，箱子的一个壁上开着一个小孔，小孔上装着一个用计时装置来控制其启闭的快门。通过挂在箱子下面的砝码和装在箱子侧面的指针，就可以测定整个箱子的总重量。爱因斯坦设想，快门从时刻t1打开到时刻t2关闭，中间经历的时间Δt=t2－t1很短，以致只有单独一个光子从箱子中放出。在t1之前和t2之后，都可以要多准确就多准确地测定箱子的重量，并从而根据质量和能量的关系式E=mc2来计算出箱子在发射光子以前和以后的能量之差，它也就是这一个光子的能量。另一方面，按照计时装置的读数也可以要多准确就多准确地确定光子的发射时刻。这样，按照爱因斯坦的想法，就可以得出在准确的时间释放出准确的能量的结论，关于能量和时间的测不准关系也就不能成立了［2］388－389。爱因斯坦的这个反驳测不准关系的“光子箱”理想实验通常被称为“光子箱悖论”，这是因为:如果对于一个事实的分析，这样分析会得到一个结论，那样分析又会得到另外一个结论，而这两个结论又是矛盾的，这样的情况就叫做悖论，或者佯谬。“测不准关系”是海森堡通过其他实验的分析得到的一个结论，而“光子箱”实验却得出了一个完全相反的结论，这样就构成了悖论。悖论被解决的过程就叫做解悖。

玻尔被爱因斯坦提出的问题真的给难住了，一时无言以对。据现场目击者回忆，爱因斯坦的这个问题完全出乎玻尔的意料，以致使他大吃一惊。当时玻尔“面色苍白，呆若木鸡”［3］389。然而经过一个不眠之夜的紧张思考，终于找到了解决问题的办法。玻尔发现:这个实验未考虑到广义相对论的引力红移效应。这样，玻尔用爱因斯坦自己建立的理论解决了爱因斯坦所提出的问题。

3 玻尔的应战——解悖

第二天一早，玻尔就在会议上发言，他首先在黑板上画了一幅图2那样的示意图，这实际上就是昨天爱因斯坦那幅草图的改进。从箱子上标尺指针的位置，可以测定盒子的质量变化即能量变化——也就是光子的能量。时钟则可以测定发射光子的时间。

他论证说，爱因斯坦在这里竟完全没有注意到，在他的广义相对论中有一个很重要的推论，那就是“红移效应”，解决爱因斯坦这个“光子箱”疑难的关键就是引力红移效应。引力红移效应，曾经作为检验广义相对论正确性的三大经典实验之一而广为人知。

所谓“引力红移”就是:当单色光通过一个不均匀的引力场时，因为各处的引力场强度不同，可以发现在不同地点处光的频率是不同的。当从引力场强的下方传播到引力场弱的上方时，由于光子向上运动要克服引力势能，本身能量减小，所以它的频率就要减小(光子的能量ε=hν)，光谱线将向低频率的红色方向移动，这种现象就叫做光谱线的引力红移［4］175。由于周期与频率成反比，所以位于不均匀引力场中的钟，在各处走的快慢就不一样，引力场越强的地方，时间就变得越慢。

玻尔指出，这正是解除爱因斯坦“武装”的关键所在。他高兴极了，简直有点幸灾乐祸的味道，因为广义相对论的创立者竟然“忘记”了自己亲手创建的新理论，这简直太好玩了。如艾萨克森在《爱因斯坦:生活和宇宙》中所说的:“(你的)新理论已经‘背叛了’你自己的广义相对论。”于是，玻尔在会上对爱因斯坦的论证进行了有力的反驳。根据爱因斯坦的广义相对论，在钟沿重力方向发生位移的过程中，它的快慢是会发生变化的。因此，由钟所读出的时间就会由于光子的逸出和箱子的位移而有一个不准量，它与光子能量不准量的乘积正好就满足测不准关系。下面就是它的这个简单推证［5］61。

设在快门开启后，箱子上升Δx距离。从箱子中发射的光子，由于箱子向上运动Δx距离，其频率要减小，相应的能量要下降如果设光子的频率在初、末态分别是ν和ν'，则由光子的能量守恒

移项可得:

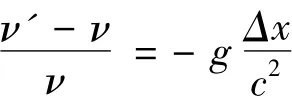
因而光子频率的相对不准量就是:

对于箱子中的时钟，也会发生类似的情况。在引力方向移动一段距离Δx时，时钟的快慢会改变。根据广义相对论，它的读数在一段时间间隔t内，将相差一个量Δt，考虑到时间周期和频率的关系则有

从式(1)就有:

对箱子的任一测定，由于位置的任一不准量Δx，必然带来箱子动量的不准量Δpx，这个不准量Δpx一定不会大于在称重量的这段时间t内，引力场所能给予一个质量为Δm的物体的总冲量(注意到在无摩擦的情况下有动量定理:动量的增量等于它所受到的冲量Ft)，即Δpx≤Δmg·t

这也就是

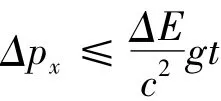
则有

将式(2)代入式(3)，即得

这就是在光子箱的称量过程中，时间测量的不准量Δt与能量测量的不准量ΔE之间的关系，而这正是我们所熟知的时间和能量之间的测不准关系。

由此可见，如果用这套装置精确测量光子的能量，将不能准确控制光子逸出的时间，反之亦然。它们的不准量之间的关系再次得到和“测不准关系”相一致的结果，这正是时间—能量之间的海森堡测不准关系式(4)。

光子箱悖论及其解决是一个关节点。爱因斯坦终于承认了玻尔对量子力学的解释不存在逻辑上的缺陷，从此以后，他的主攻方向就从试图找出量子力学理论体系的不自洽性，转到试图证明量子力学的不完备性上去了。

4 从“光子箱悖论”得到的启示——塔尔斯基型解悖

“光子箱悖论”本来是爱因斯坦为了反驳测不准关系而提出的一个理想实验。所谓理想实验，也叫做“思想实验”或“假想实验”，就是那些在理论原则上可以实现，而实际上却很难具体操作的、只能在想象中进行的实验。在近代物理学的发展过程中，由于研究对象的高速、微观等特征，离人们在实验室中可以直接操作的对象越来越远，所以理想实验就发挥着极其重要的作用。

按照爱因斯坦原来的设想，在这个光子箱实验中，应该既能准确测定一个光子逸出光子箱的时间，又能准确测定光子箱在这个时间的能量变化，从而测不准关系不成立。可是通过玻尔的分析，如果考虑到在引力场中时间快慢变化的相对论效应，那么时间测量和能量测量的不准量之间，正好就有一个符合海森堡测不准关系式的关系存在。

分析爱因斯坦“光子箱悖论”的解悖过程可以发现，整个事件曲折离奇，富有戏剧性，也极富想象力。有人就一直在想，如果爱因斯坦本人晚几年才发现和发表他的广义相对论，那一切又会是一个怎样的结果呢?如果没有广义相对论，只在牛顿力学和麦克斯韦电动力学的范畴内，甚至也包括狭义相对论，都是无法解决这个疑难的。只有在一个更高层次的理论中，低一个层次的悖论才能得到很好的解决。狭义相对论将相对性原理从力学现象推广到包括力学和电磁现象的一切物理现象，广义相对论则进一步将相对性原理从惯性系推广到包括非惯性系在内的一切参考系，从这个意义上来说，广义相对论是狭义相对论的直接推广。狭义相对论以前的理论适用的是惯性系所在的平直时空，而广义相对论则是适用于一切参考系的弯曲时空的理论，从这个意义上来说，广义相对论也是狭义相对论的自然推广，它是比狭义相对论更高一个层次的理论。如果把相对论加以形象化，它好比是一座两层楼。底下一层是狭义相对论，上面一层就是广义相对论。相对论作为一个整体包括狭义相对论和广义相对论两个部分，两个层次。狭义相对论是广义相对论的基础，广义相对论则是狭义相对论的发展，标志着“更上一层楼”［6］63－64。

“光子箱悖论”的这种解悖方法告诉我们，在一个大的统一的理论中可能有不同的层次。在低层次中的悖论，在高层次中可能就不再是悖论了。而这种用分层来解悖的方法与著名的“说谎者悖论”的解悖方法有异曲同工之妙，都属于一种“塔尔斯基型解悖”。

“说谎者悖论”曾经被认为是人类历史上最迷人的十大不解之谜之一。它是古希腊哲学家伊壁孟德(Epimenides，公元前6－5世纪)提出来的，这个悖论是这样的［7］148:如果他说:“所有的克里特人都是说谎者。”那么，伊壁孟德说的这句话是真的吗?如果是真的，那么他本人就是克里特人，他也是说谎者，则这句话是假的;如果是假的，那么作为克里特人的伊壁孟德是说谎者这一点也就是假的，则他所说的“所有的克里特人都是说谎者。”这句话就是真的。结果是矛盾的。这个悖论也可以这样表述:“克里特岛的一个人说:‘克里特岛人都在说谎。’那么这个人是否在说谎?”如果他说的是真话，由于他也是克里特岛人之一，他也在说谎，因此他说的是假话;而如果他说的是假话，则说明有的克里特岛人不说谎，他也可能是这些不说谎的克里特岛人之一，因此他说的就可能是真话。那么，他说的到底是真话还是假话?似乎两个结论都对，但这是完全相反的矛盾结果，不可能都对，这就构成了悖论。后来，“说谎者悖论”有了一个更简练的版本:“我现在说的这句话是假话。”那么，这句话究竟是真话还是假话?如果是真话，他明明说这句话是假话;如果是假话，那么假话的假话就是真话，结果是真话。这就构成了悖论。

这种悖论究竟是如何产生的?又如何去克服和避免?长期以来一直莫衷一是，没有一个非常令人满意的结果。

但仔细分析就会发现，在“说谎者悖论”中，“我说的这句话是谎话”中的“这句话”与整个这句话，是两个不同层次的语句。把“这句话”与“我说的这句话是谎话”的这句话混同了起来，就构成了悖论。如果把这一点分清楚，在高一层次的语言角度上去理解低一层次的“这句话”，就不会有矛盾了。

这种分层次的解悖方法，我们就把它称为“塔尔斯基型解悖”或“塔尔斯基模式”［8］146。

阿尔弗雷德·塔尔斯基(A.Tarski，1902－1983)是一位波兰裔美国哲学家、逻辑学家和语言学家。他对说谎者悖论进行了认真地分析研究。他认为这种语义悖论产生的根源是混淆了语言层次，解悖的方法是将语言分层［9］141。1931年，塔尔斯基在《形式化语言中的真概念》一文中，提出了“语言层次”的理论。他指出:要建立实质上正确的关于“真句子”的定义，就必须对语言进行分层处理:被谈论的语句属于某一层次的语言(称为“对象语言”)，而陈述该语句语义性质的语句则属于高一层次的语言(称为“元语言”)［10］247。按照语言层次理论的要求，若不考虑语言的层次划分和各层次语言的作用，就不能得出语句的真定义，即用元语言去陈述对象语言或用对象语言去判定元语言就会产生思维混乱，严重的就会形成悖论。

“说谎者悖论”就是因为断言了自身的真假，混淆了语言的层次而造成的。这类悖论的核心在于“自我指涉”，也就是涉及到自我指称的问题，即说话的那个人说的话是说自己。这句话中所说的“这句话”是对对象的陈述，属于对象语言。而陈述该语句语义性质的语句如“真的”“假的”这样的语义表达式，是属于元语言。如果不能明确地区分对象语言和元语言，混淆了语句的判定作用，句子将变得无意义。塔尔斯基主张，为了避免这种混乱，必须要清楚地把某层次的对象语言和对其进行判定的元语言区别开，这种解决悖论的方法就是对语言分层。

“光子箱悖论”的解悖方法也是将理论分层，分层的目的是搞清楚论辩双方各自依托的基础理论的内涵之间的联系。在低层次理论中的悖论，在高层次理论中就不再是悖论了，高一层次的广义相对论解决了较低层次的狭义相对论依托的理论所存在的悖论(引力红移在狭义相对论中不可能出现)。“说谎者悖论”的解悖方法是将语言分层，分层的目的是要消除对象语言和元语言的混淆，从而避免语言上的逻辑悖论。用高一层次的元语言对较低层次的对象语言进行判定，从而使悖论得到解决。可见，它们在解决悖论的思想方法上有共同之处。解悖的关键都在于分层。因此，对理论进行分层的“光子箱悖论”的解悖，可以看成是塔尔斯基用语言分层来对“说谎者悖论”解悖的一种推广，扩大了塔尔斯基分层型解悖的适用范围，将其归结成为一种“塔尔斯基型解悖”的模式。

这种“塔尔斯基型解悖”还可以用于对波粒二象性的理解。微观客体的波粒二象性在经典理论中是一个不合理的悖论，结果构成了所谓“波粒佯谬”(佯谬和悖论是同一个意思，在英文中都是paradox)。而在较高层次的量子理论中它则是自洽的量子力学理论的一个基本事实。正是区分了理论的层次，波粒佯谬自然得到了解决。这也是应用“塔尔斯基型解悖”的一个范例。

在科学发展中出现的悖论是各种各样的，而其中很大一部分都可以用“塔尔斯基型解悖”来解决，因此这种方法是有普适性的。

爱因斯坦和玻尔都已经远去，他们所争论的关于量子理论的对与错人们现在还在继续评说。人们对于物质和世界本原的认识，是没有止境的，他们那一代科学家追求真知的诚挚态度，永远都值得我们尊敬和钦佩。无论是从他们对于科学的贡献来说，还是他们的科学思想和科学方法，乃至作为科学家的高度社会责任感和正直品格，都是我们学习的榜样。长路漫漫，我们需要一个又一个像玻尔与爱因斯坦那样的伟人!

［1］方励之.惠勒演讲集:物理学和质朴性［M］.合肥:安徽科学技术出版社，1982.

［2］N玻尔.作用量子和自然的描述［C］//戈革，译.尼耳斯·玻尔哲学文选.北京:商务印书馆，2009.［3］戈革.尼耳斯·玻尔——他的生平、学术和思想［M］.上海:上海人民出版社，1985.

［4］韩锋.广义相对论:及其思想和方法的评述［M］.乌鲁木齐:新疆教育出版社，2003.

［5］N玻尔.原子物理学和人类知识［M］.郁鞱，译.北京:商务印书馆，1964.

［6］舒炜光.爱因斯坦问答［M］.沈阳:辽宁人民出版社，1983.

［7］马霍尔·丹纳斯.说谎者悖论和汉诺塔游戏［M］.程云琦，译.沈阳:辽宁教育出版社，2006.

［8］吴学谋.泛系·不合上帝模子的哲学［M］.武汉:武汉出版社，1996.

［9］刘源沥.诡辩之谬:使言语有力的艺术［M］.三重:新雨出版社，1984.

［10］陈波.逻辑哲学导论［M］.北京:中国人民大学出版社，2000.

［责任编辑刘景平］

Einstein’s“Photon Box”Paradox and Tarski’s Type Method of Solving the Paradoxes

HAN Feng
(Department of Physics and Electronic Engineering，Hechi University，Yizhou，Guagnxi546300，China)

“Photon box”paradox is the key issue of the argument between A．Einstein and N．Bohr．By analyzing Einstein’s“photon box”paradox and the process of solving the paradoxes，the enlightment from the methods for solving paradoxes is explored，that is，they are solved bymeans of the stratified methodswhich Tarskis put forward．It is of great significance to deeply understand Tarski’s stratified methods for solving paradoxes and develop it into the universal ones．

A．Einstein;N．Bohr;photon box;Tarski’s typemethod of solving the paradoxes

book=0,ebook=82

O413

A

1672－9021(2012)02－0001－06

韩锋(1943－)，男，山西文水人，河池学院物理与电子工程系教授，主要研究方向:理论物理学和物理哲学。

河池学院科研基金资助课题(2011B－N001)。

2012－03－11