论波粒二象性及测不准关系

张佳林

（湖南师范大学 物理与信息科学学院，湖南 长沙 410081）

1.粒子与波的概念

在哲学上常说：世界的本质是物质，物质是构成整个世界的基础。当然这里所指的“物质”是哲学上的广义的物质，其具体特征是具有客观和实在性，然而在物理上，我们经常听到，物质是有很多粒子构成的。粒子的英文单词是particle,其本意是非常小的块或部分，即能够以自由状态存在的最小物质组分。最常见的粒子是电子，质子和中子，后来随着实验的进步，越来越多的更小的粒子被发现了，累计已超过几百种，且还有不断增多的趋势，如：μ子、τ子、中微子等等.但这样的话，给人感觉整个物质是可以无穷的细分下去，正如1除以3永远除不尽一样。人们直观上认为任何粒子都应该存在某种固定的边界和尺寸，但是在相对论里面存在着一种情况，就是粒子各部分运动速度不相同，此时粒子的固定边界或尺寸就不再严格成立，因此粒子就变了。所以，直观上粒子的概念未必总是完美的，它在不同的时空背景中是不同的，而在量子力学里面，它的定义及处理上会也更加的特殊，与我们原来直观认为（非常小的块或部分）不同，它的数学定义是一种几率波包。

波，一提起这个字，就很容易让人形象的想起水波起来。确实，水波和声波是最常见的机械波，很清楚也很明白；而对于一些非机械物质波，人们似乎就很难想象不出来。波是物质本身运动的结果，它是物质运动状态的传递，其行为要满足波动方程。但是，令人吃惊的是，这个世界往往将两个似乎不相关的东西紧密联系了在一起——物质不仅具有粒子性还具有波动性。

2.波粒二象性提出

波粒二象性的提出，要从人们对光的认识开始谈起。在早期存在两个观点：一是以牛顿为代表的光的粒子学说；二是以胡克（Hooke）和惠更斯（Huygens）为代表的光的波动学说。两者争论不休，各有支持者，到了二十世纪初，普朗克（Planck）为了克服经典理论解释黑体辐射规律的困难，引入了能量子概念，为量子理论奠下了基石。爱因斯坦（A.Einstein)针对光电效应实验与经典理论的矛盾，提出了光量子假说，并在固体比热问题上成功地运用了能量子的概念。光的波动说与微粒说最终以“光具有波粒二象性”而落下了帷幕。1924年，德布罗意(de Broglie)提出了德布罗意假设，声称所有的物质都有类波的特点：λ=h/p， 其中λ为波长，p为动量，h为普朗克(Planck)常量。三年后，德布罗意(de Broglie)的假设通过两个独立的电子散射实验而被证实。1929年，他也因此而荣获诺贝尔物理学奖。这就是说客观的物质不仅具有粒子性还具有波动性。

3.测不准关系

测不准关系即测不准原理是由海森伯(Heisenberg)于1927年首先提出的。他最初的思考也是源于他在创建矩阵力学时，既要否定在人们脑海里已经固化了的不正确物理图像，同时又不得不借助已有的概念来说明（坐标，速度，动量等），只是这些词汇的含义与原来的有些区别，有某些限制，这些限制就包括测不准原理。什么是测不准原理呢？测不准原理也叫不确定原理，它是指在量子物理里面，一对正则共轭变量的数值是不能同时被准确的测量。例如：动量和坐标就是一对正则共轭变量。那么测不准关系就可具体表述为：描述微观粒子的坐标和相应动量不可能同时具有确定其中Δx为位置的不确定量，为动量的不确定量，h=2πħ是普朗克常数。类似的这种不确定关系还存在于时间和能量，角动量和角度等其它的一些正则共轭变量之间。可以说，测不准原理反映了微观粒子运动的基本规律，是物理学中又一条重要原理，它还是物质波粒二象性的重要体现。

4.波粒二象性与测不准关系

为了更好的理解和说明测不准关系，根据物质波粒二象性，我们可以利用简单的平面波函数来简单的证明和诠释。

在量子力学里面有五个最基本的假设，而其中就有，微观体系的状态是用波函数来描述的，而任何经典力学量都用相应算符来表示。需要指出的是，根据玻恩(Born)提出的“概率波概念”，此时的波函数是作为几率波来理解的（粒子被发现的几率等于此波函数模的平方），而微观粒子的处理上与我们原来直观认为（非常小的块或部分）不同，它的数学定义是一种波包。其实，这也很好理解，由于波函数是作为几率波来解释的，那么波包就表示在这个地方发现粒子的几率最大，当然就认为粒子在那个地方，它在数学上就可以表示粒子了。这也正是数学上处理波粒二象性的方法。

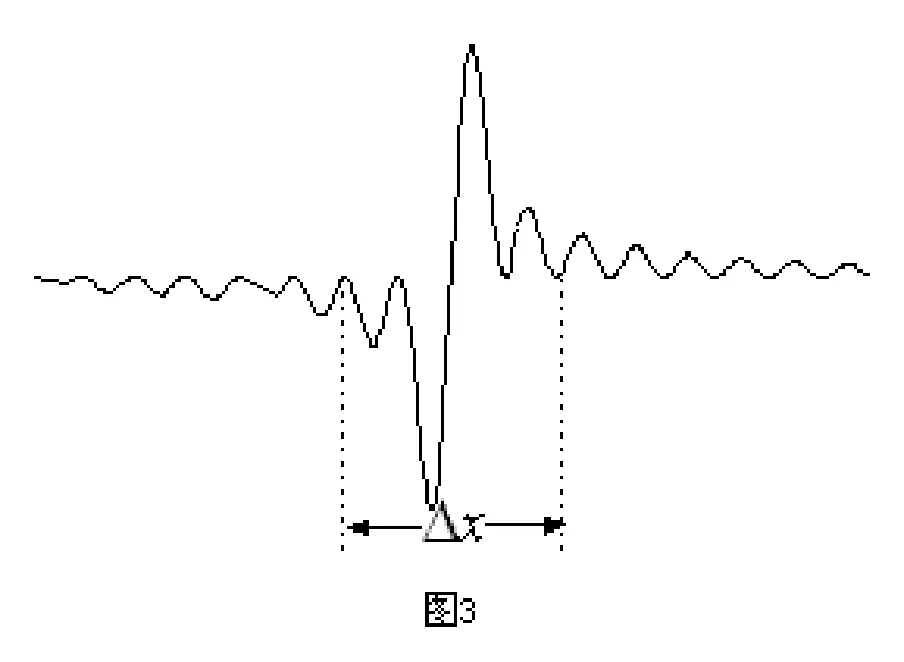
如果再加入更多的不同波长的平面波函数 ，并选择合适的相位和相同的振幅，我们会发现，Δx的宽度将会越变越小，而突起的幅度变的很大，同时Δx区域以外的振幅几乎为零（如图3）。在这里，我们就会发现一个规律：加入的不同的波长的平面波越多，Δx就变的越小，而只有一列平面波时，Δx是等于零。假如我们用Δk来表示波数的变化范围的话，就近似有如下关系：，再根据德布罗意(de Broglie)的物质波假设很容易的到：这跟实际精确的理论推导公式很接近了。

现在，我们再来分析此过程。当只有一列平面波的时候，我们在任何地方都可以找到某粒子，也就是说在任何地方找到它的几率是等同的，此时的动量是确定的（因为只有k1），但是，粒子的位置是不确定的，因为它可以出现在空间任何地方。而一旦要知道粒子准确位置，即要在空间中某点只有一个特别陡峭和狭窄的波包，就必须要有很多的不同波长（动量）的波叠加才行，这也就是说我们要特别精确的知道粒子处于坐标空间的某点，就必须在牺牲粒子动量的准确度下才可以做到。

从上面的描述推理过程中，很容易知道测不准原理并不是与你的仪器设备相关，它的核心和基础是来源与“波粒二象性”。只要物质存在“波粒二象性”，测不准关系就必然成立。因此，提出“微观粒子在空中某一点的动量”是没有意义的，其错误就类似于说“在空间某点处的波长”一样。此外，由于测不准关系的存在，我们以前所认识的粒子运动轨迹的说法也不再成立了，这也就是说粒子是没有运动轨道的，它只是有可能以某种几率 出现在空间某个地方。这些于日常生活中观念很有相矛盾，是让人很难接受的。但是，对于现实生活中的宏观事物，我们是不是也需要调整原来那已经根深蒂固的说法呢？其实是不需要的。这是因为那个普朗克常量h是一个很小的物理量，宏观现实中，人们至今所做过的一些精确测量所得到 Δx 和Δp的乘积都远远大于普朗克常量。因此，对于一般的宏观研究对象，我们依然可以使用轨道以及某点的动量这种经典的提法。与此类似，能量和时间也存在这样不确定关系，即

总之，量子力学里面测不准关系是与人们直观感觉相矛盾的，很多人对此感到迷惑以及误解，其实人们很少看到测不准关系核心本质是物质具有波粒二象性。本文通过简单的平面波叠加原理及波包知识就很简单的诠释了波粒二象性及测不准原理的内在关系，有助于加深人们对这个测不准原理的理解。此外，可以发现自然界中一些看似不怎么相关的事物，有时候往往存在内在联系，而这种联系是可以通过另一种思维方式和一些数学技巧来展示出来。虽然事物的本质和客观规律是唯一的，但是描述它所需的辅助手段和借助的数学方法可以是不同的，如果能找到一个很合理数学表达方式，那将会事半功倍。

[1]郭奕玲,沈慧君.物理学史[M].北京:清华大学出版社,1993.

[2]吴大猷.物理学的历史和哲学[M].北京：中国大百科全书出版社，1997.

[3]董光璧,田昆玉.世界物理学史[M].长春：吉林教育出版社，1994.

[4]申先甲.物理学史教程[M].长沙：湖南教育出版社，1987.

[5]曾谨言.量子力学(卷II)[M].北京：科学出版社，2000.

[6]Werner Heisenberg.Physics and Philosophy[M].New York：Harper & Row Publishers, 1962.

[7]Ian D Lawrie.A Unified Grand Tour of Theoretical Physics[M].London：Institute of Physics Publishing Ltd，2002.