不定式的极限问题

王晓英，张洪光

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

不定式的极限问题

王晓英，张洪光

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

不定式的极限是极限计算问题的难点，结构复杂、形式多样，没有统一固定的计算方法，可以用初等变换消去零因子、洛必达法则、无穷小代换等，有时候一道题目需要结合使用多种方法，才能化繁为简，快捷有效的得出结果.本文根据题目的具体形式，重点介绍洛必达法则和无穷小代换的适用情行、注意问题和使用技巧，使学生对计算不定式的极限问题有更深入的理解.

极限；不定式；洛必达法则；等价无穷小

1 关于洛必达法则

定义1当x→a（或x→∞）时，f(x)→0且g(x)→0的极限可能存在，也可能不存在，通常把这种极限叫型不定式.

在所有的高等数学和数学分析教材里，一般都给出四种不同形式的洛必达法则，并用中值定理加以证明，如复旦大学《数学分析》（第三版）237页，同济大学（第五版）133页，本文概述如下；

（2）f与g在x0的某空心邻域U0(x0)内可导，且g'(x)≠0；

注2定理中的“x→x0”换成“x→±x0、x→±∞、x→∞”只要修改相应的条件（2），也得到同样的结论.

注4只要f'，g'，f"，g"，f苁，g苁…满足定理条件，洛必达法则可以重复使用.在多次应用洛必达法则时，使用前要检查是否仍满足洛必达法则条件，否则会出现错误，例如，但若两次用洛必达法则就得错误结果.原因是当x→∞时，c o s x不存在极限，此时不满足洛必达法则的条件（2）.利用洛必达法则求极限的时候应该注意

注5 洛必达法则是处理未定式极限的重要手段，且非常有效.但它只能直接应用于型和型的未定式.而对于∞-∞,0·∞,∞0,1∞,00等形式，需化为型和型求解.一般的∞-∞可以通分化为标准型;而∞0,1∞,00一般先取对数化为0·∞型进而化为标准型.

解（1）当x→π时，f(x)=1+c o s x和g(x)=t g2x都趋于零，由洛必达法则得

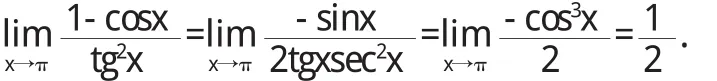
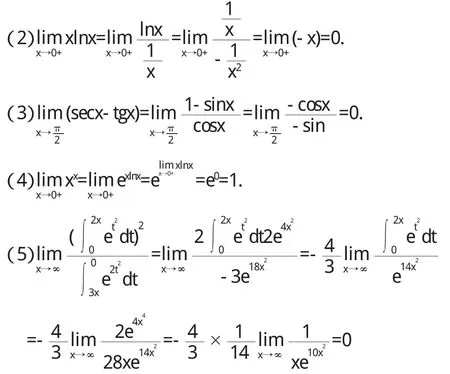
=3，试求f'(0).

解 因为

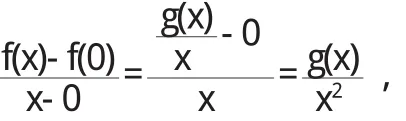
所以由洛必达法则，得

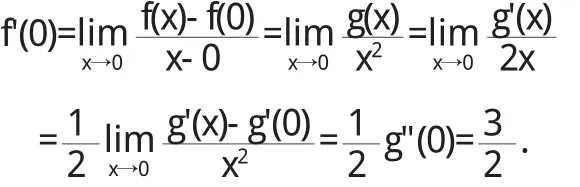
连续两次用洛必达法则的做法是错误的：

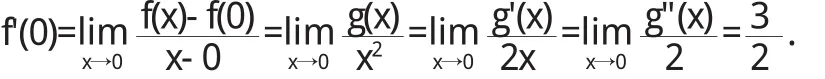
原因在于题设条件只有g在x=0存在二阶导数，不知g在x=0的某邻域内是否也存在二阶导数，更不知二阶导数在x=0是否连续.

注6 用洛必达法则求数列的极限 用洛必达法则求函数的极限，要求函数在点的邻域内可导，数列的极限问题，由于不满足洛必达法则条件，不能直接用洛必达法则计算，有时可以转换为函数极限问题，进而求出数列的极限.

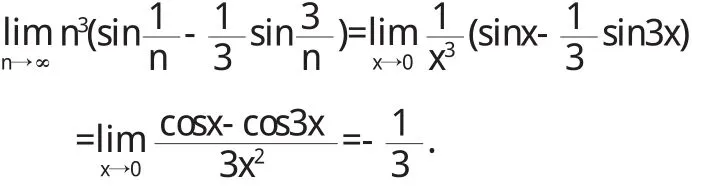
2 关于无穷小等价代换

无穷小具有很好的性质，在求极限的运算过程中，掌握并充分利用好它的性质，往往会使一些复杂的问题简单化，可起到事半功倍的效果.但代换不当时会产生错误.利用无穷小量的代换性质求函数的极限，即将分式函数中的分子、分母，用与其等价的无穷小量来代换.

定义2 在某一变化过程中，以零为极限的量称无穷小

定义2'如果数列{an}当n→∞时的极限是零，则称数列{an}为当n→∞时的无穷小.

定义2"如果函数f(x)当x→x0(或x→∞)时的极限是零，则称函数f(x))为当x→x0(或x→∞)时的无穷小.

定理2 设α,α',β,β',γ等均为同一自变量变化过程中的无穷小，则

（2）若α~β，β~γ，则α~γ,（3）若α~α',β~β'，且l i m=c(c≠-1)，则α+β~α'+β'

定理3 设在自变量的某一变化过程中，α(x)、β(x)、α (x)、β'(x)都是无穷小量.

（1）若α~α'，g(x)为同一过程中的另一函数，且l i m α'g(x) =A，则l i m αg(x)=A

（2）若α~α',β~β'，f(x)为同一过程中的另一函数，且l i m存在，则也存在，且

定理4 设在自变量的某一变化过程中，α(x)、β(x)、α (x)、β'(x)都是无穷小量.

（1）若α~α',β~β'，则对于未定式1∞型有：

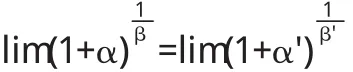
证明 （1）在自变量的某一变化过程中

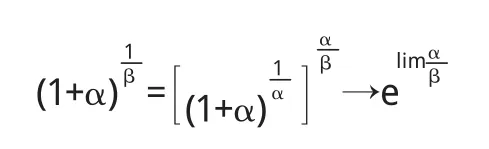
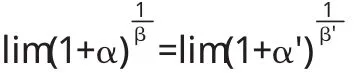
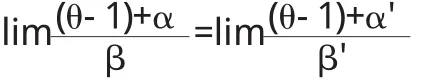
常用的等价无穷小（x→0,a>0且a≠1,α为常数）.

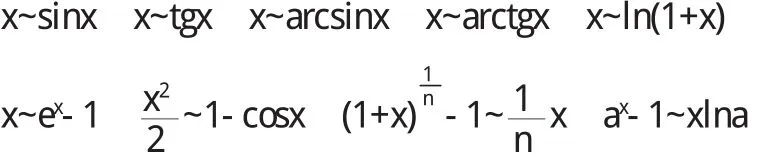
解 因为x→0时当a r c s i n 5 x~5 x,a r c t a n 2 x~2 x,s i n 3 x~3 x，而且所以原式

解 因为当x→0时a r c s i n 3 x~3 x,c o s 2 x→1，而且,所以

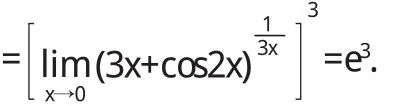
以上例子说明等价无穷小量的代换方法对求函数的极限起到了简化运算过程的作用，将一些不易求解的极限问题化繁为简，化难为易，从而得到解决.因此，掌握以上方法，可以使得函数极限的计算更加容易.

3 有效结合多种方法，选择最优解决途径

洛必达法则和等价无穷小代换都是解决不定式极限的常用的有效方法，但都有一定的局限性.利用无穷小量的代换性质求函数的极限，能使问题简化，但是涉及代数和或部分代换时容易出现错误，使用时需要谨慎.洛毕达法则也不是万能的，更不一定是最佳的，有时尽管满足条件，但把式子越变越复杂，难于求出最后的结果.如计算应用洛必达法则有

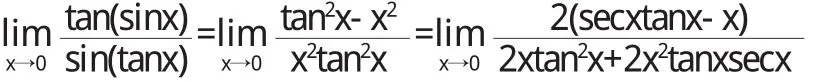
继续下去表达式会更加复杂.很多时候需要几种方法结合起来运用，包括初等变形、洛必达法则、等价无穷小代换、级数展开等.

解因为当x→0时s i n x~x,t a n x~x,ex-1~x

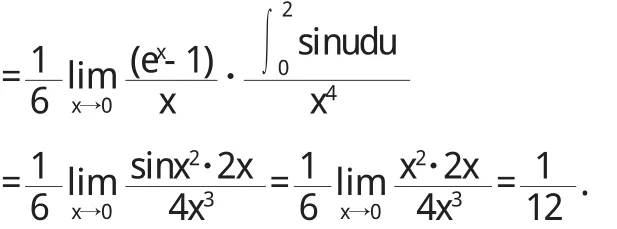
〔1〕同济大学数学教研室.高等数学(上册)[M].北京:高等教育出版社，1996.

〔2〕杨文泰，等.价无穷小量代换定理的推广.甘肃高师学报，2005，10（2）：

〔3〕汪荷仙.高等数学解题方法指导[M].成都:成都科技大学出版社，1995.

O 13

A

1673-260X（2012）10-0007-03