一类门限签名方案的密码学分析与改进

禇晶晶，于秀源

（1.杭州师范大学理学院，浙江杭州310036；2.杭州师范大学护理学院，浙江杭州310036）

一类门限签名方案的密码学分析与改进

禇晶晶1，2，于秀源1

（1.杭州师范大学理学院，浙江杭州310036；2.杭州师范大学护理学院，浙江杭州310036）

2008年，XIE等人提出了一种新的基于模秘密共享的门限签名方案，即利用孙子定理来实现秘密共享的门限签名方案.该文指出XIE等人的方案是不安全的：任意t人与DC合谋即可生成一个有效的门限签名并嫁祸给他人；任意少于t人联合DC也可生成一个有效的门限签名.为克服该方案的安全性弱点，给出了一个改进的方案.

门限签名；秘密共享；模秘密共享；合谋攻击

0 引 言

（t，n）门限签名最早由Desmedt和Frankel［1］提出，其中t＜n，它是指由n个成员所组成的可参与签名群中，任何t个或t个以上成员才能代表该群体生成一个有效的签名（若有多于t个人想签名，只需其中的t个人签名即可），任何少于t个人所生成的签名是无效的.门限签名具有对签名验证人的匿名性及对可信中心的可被追踪性.

直到现在，门限签名得到了广泛的研究，提出了各种各样的门限签名方案.有基于离散对数及二次剩余难解问题的［2］，有基于大数因式分解难解问题的［3］，也有基于椭圆曲线体制的［4］，但不论是基于何种数学难题的门限签名都要以秘密共享作为它的基础.门限秘密共享［5］的主要思想是将一个密钥分成若干子密钥分配给各个成员保管，当需要重构密钥或使用它进行某种密码运算时，必须多于特定数量（门限值）的成员才能共同完成，少于特定数量的任何成员组都不能计算得到此密钥.

XIE等人在文献［6］中指出文献［7］［8］等很多基于拉格朗日插值共享的签名方案是不能抵抗合谋攻击后，又在Asmuth-Bloom模秘密共享思想［9］的基础上提出了新的基于模秘密共享的门限签名方案［6］.本文指出，文献［6］的方案也是不安全的，该方案也不能抵抗内部成员的合谋攻击，而且可以利用合谋得到的群密钥进而伪造签名并嫁祸他人.为克服他的安全性弱点，本文给出了一个改进的方案，分析表明，本改进方案是安全的.

1 XIE等人方案简介［6］

XIE等人方案由系统初始化、部分签名的生成、门限签名的生成、门限签名的验证4个阶段组成.

1.1 系统初始化阶段

（1）可信中心TC选取两个大素数p和q，q｜p-1，g是GF（p）上阶为q的生成元，即gq≡1（modp），H（·）是一个安全的单向Hash函数.设可参与签名的群体中有n个成员，用集合G＝｛U1，U2，…，Un｝来表示该群体的所有成员.该群体中任何t个或t个以上成员可代表该群体进行签名（若有多于t个人想签名，只需其中的t个人签名即可）.

（2）可信中心TC随机选取x∈RZq作为系统的群私钥，y≡gxmodp则为系统的群公钥.

（3）可信中心TC选取一个素数r（r＞x），一个正整数s以及n个正整数m1，m2，…，mn，它们满足以下条件［9］：①gcd（mi，mj）＝1，i≠j，i，j＝1，2，…，n；②m1＜m2＜…＜mn，rm1m2…mn；③m1m2…mt＞rmnmn-1…mn-t＋2；④m1m2…mt＞x＋sr＞mnmn-1…mn-t＋2；⑤L［m1m2…mt］＞L［p］＋L［q］.其中L［x］代表x的长度.

（4）TC为每个Ui（i＝1，2，…，n）计算秘密钥xi≡x＋sr modmi，Ui的公开钥为yi≡gximodp.

（5）TC将xi通过秘密信道发送给各个Ui，公开p，q，g，H（·）及y，并将s，r，mi（i＝1，2，…，n）和yi（i＝1，2，…，n）存入一个只有群成员可以访问的记事本①yi（i＝1，2，…，n）既然已经公开，那这里所说的将它们也“存入一个只有群成员可以访问的记事本”就没有意义了..

1.2 部分签名的生成阶段

（1）设参与门限签名的t个成员是U1，U2，…，Ut，要签名的消息为M.每个Ui随机选取ki∈RZq，并计算和广播ri≡gkimodp给其他成员.

（2）每个Ui计算以及）＋kiR（mod m1m2…mt），其中Mi＝m1m2…mi-1mi＋1…mt，M-1iMi≡1modmi.将（（ri，ai），M-1i，Mi，mi，s，r）发送给指定的签名收集者DC.

1.3 门限签名的生成阶段

于是，（A，R）是对消息M的门限签名.

1.4 门限签名的验证阶段

门限签名的验证人收到（A，R）后，通过下面的等式来验证签名的正确性：yH（M，R）RR≡gAmodp

2 对XIE等人方案的密码学分析

本节给出了对XIE等人方案中群私钥x的合谋解密攻击、个人私密钥xi的合谋解密攻击、任意t人联合DC嫁祸他人的合谋伪造攻击和任意少于t人联合DC的合谋伪造攻击.

2.1 群私钥x的合谋解密攻击［10］

由1.1（5）可知，对于可参与签名的群成员Ui来说，mi（i＝1，2，…，n）及s，r是可以通过访问文件得知的，是不保密的.设参与过某次门限签名的t个成员是Ui1，Ui2，…，Uit，若该小组成员徇私共谋，各自在这一小组内部公开自己的私钥，即可很容易地按照下面的方法求出群私钥x：

设这t个私钥是xi1，xi2，…，xit，则由孙子定理可知，存在唯一的x0，0≤x0＜mi1mi2…mit，满足方程组

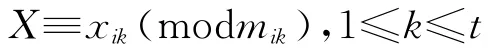
显然x＋sr满足上述方程组，而且由于r＞x及s的选取方式（见上文1.1（3）④），可知

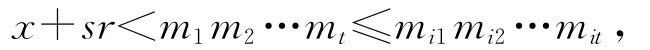
因此，必是x0＝x＋sr，即x＝x0-sr是唯一确定的.

2.2 个人私密钥xi的合谋解密攻击

合谋小组由已获得的群私钥x及可访问的存有mi（i＝1，2，…，n）等信息的文件，利用等式

xi≡x＋sr modmi就能解得xi1，xi2，…，xit以外的任意一个个人私钥xij（j＝t＋1，t＋2，…，n）.

2.3 任意t人联合DC嫁祸他人的合谋伪造攻击

2.3.1 部分签名伪造阶段

如果上述共谋获取群私钥的t个成员希望某个文件可以被签名验证通过，又不想在某些意外情况下承担责任，让追踪者追踪不到自己而嫁祸给别人，即可进行以下签名（当n≥2t时，合谋伪造尤其容易发生，因为合谋小组里的任何一个成员都可以逃脱意外发生时的追踪，从而嫁祸给他们这t个成员以外的可参与门限签名的另外t个成员）：

（1）设意欲伪造新的门限签名的t个成员是Ω＝｛Ui1，Ui2，…，Uit｝，要签名的消息为M′.他们想要栽赃的t个成员是Λ＝｛Ui，t＋1，Ui，t＋2，…，Ui，2t｝.Ω小组（一起或者由负责人）随机选取t个kij∈RZq（j＝t＋1，

t＋2，…，2t），计算rij≡gkijmodp及

（2）然后Ω小组利用已获得的Λ小组的私钥及其他信息，计算

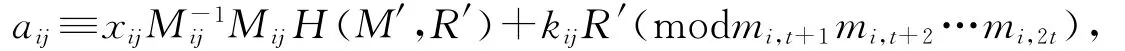
其中Mij＝mi，t＋1mi，t＋2…mi，j-1mi，j＋1…mi，2t，M-1ijMij≡1modmij.

并将（（rij，aij），M-1ij，Mij，mij，s，r）发送给指定的签名收集者DC.

2.3.2 门限签名伪造阶段②若DC事先不知道谁参与签名，则会根据mij去追踪签名人，所以在他知道了mij后，利用mij所对应的yij来进行验证，因此Ω小组可以闯过DC的验证从而借DC之手再次达到伪造门限签名的目的；若DC事先就会被告知该次参与门限签名的成员，且Ω小组说服了DC与其合谋来伪造门限签名，则仍可以继续伪造以闯过验证人的验证.

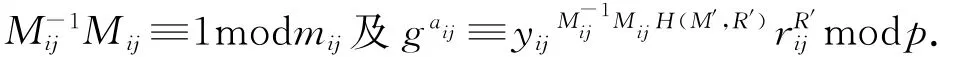
则对消息M′的门限签名是（A′，R′）.

2.3.3 伪造的门限签名通过验证阶段

验证人收到（A′，R′）后，计算yH（M′，R′）R′R′≡gA′modp是否成立，由上面的陈述可知，等式成立，所以伪造的门限签名通过了验证人的验证，伪造成功.

2.4 任意少于t人联合DC的合谋伪造攻击

验证式yH（M，R）RR≡gAmodp中不含带有签名人身份的信息，也不含数字t，因此验证人不能追踪到签名人，也不能确认是否是t个人一起签的名.只要DC同意，任意少于t个的签名人都可以与DC合谋生成一个可闯过验证人验证的签名.

3 对XIE等人方案的改进

3.1 系统初始化

（1）同XIE等人方案中1.1（1）.需要注意，改进的方案中，令n＜2 t（更安全并符合实际情形中票数过半原则），而这n个参与者其中t人参与签名的不同组合有Ctn个［11］，把群秘密分配到Ctn个不同组合中去.

（2）为这Ctn个不同组合分别构造其对应的秘密钥Ej（j＝1，2，…，Ctn），使得群秘密E是与所有Ctn个共享秘密Ej有关的和，即满足，其中f是一个关于Ej的函数.可通过下述方法来构造Ej：

首先任意选取t对不同的数mi∈RZq，xi∈RZq，mi为成员Ui的身份标识，xi为成员Ui的私密钥.利用孙子定理构造第一个子群的私密钥（mod M1），如果E1≡0（mod M1），则重新选择某个mi或xi，这样就可以得到第一个签名组共享的子秘密E1，其中③M1＝m11m12…m1t，M1i＝M1i≡1（modm1i），1≤i≤t.

继上一节t对不同数的选择后，现再取第t＋1对不同的mi∈RZq，xi∈RZq，与前面选取的任意t-1对数结合，用孙子定理构造t个Ej，j＝2，3，…，t＋1，满足所有的共享子秘密Ej≠0（mod Mj）且两两不等，任意多个的和模上M不等于零，即（modM），其中λ＝1，2，…，i在此表示不同λ个的取法标记.按照此方法，可以构造个子秘密Ej，j＝1，2，….

（4）随机选取dj∈RZq，j＝1，2，…，，计算Dj≡gdjmodp.计算群中每一个成员Ui的公钥yi≡modp，并计算组的密钥Ej所对应的≡E-Ej（mod M），再计算Rj使之满足≡Dj·Rjmodp， j＝1，2，…，.

（5）TC在系统内公开参数p，q，g，H（·），y，Dj，Mj，yi，只有系统内的成员可以访问这些数据.并将xi与mi通过秘密信道发送给各个Ui，对于任意一个Ui，可以通过验证方程yi≡gximodp是否成立来判别得到的xi是否有效的密钥.再把Rj与mi发送给DC.

3.2 部分签名的生成阶段

（1）设由群G中t个成员构成的第j个子群G0＝｛Uj1，Uj2，…，Ujt｝同意代表群体对消息m签名，则∀Uji∈G0随机选取kji∈RZq，并计算和广播rji≡gkjimodp给其他成员，i＝1，2，…，t.

（2）每个Uji计算modp以及

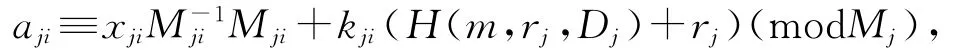
其中Mji＝Mji≡1modmji.

并将（（rji，aji），M-1ji，Mji，mji）发送给指定的签名收集者DC.

3.3 门限签名的生成阶段

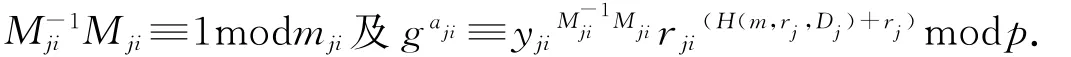
如果所有的等式都成立，则DC生成消息m的门限群签名（A，R，D）.

3.4 门限签名的验证阶段

门限签名的验证人收到（A，R，D）后，通过下面的等式来验证签名的正确性：

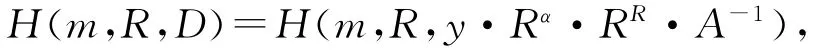
③m11，m12，…，m1t为一开始选择的m1，m2，…，mt的任意排列.为方便叙述，把上述子群记为第一组，下标第一个数字代表组号，以下将用字母j表示组号，易知j＝1，2，…，Ctn.

其中α＝H（m，R，D）.

3.5 安全性分析

（1）从以上的验证式可知，验证者根据签名无法知道哪些成员参与了签名，但在发生纠纷时TC可以通过Dj找到对应的签名成员.因此本方案具有匿名性和可追踪性.

（2）改进的方案在系统初始化阶段中使用了子群密钥的形式.在一个子群中成员只秘密掌握xi与mi，他们不知道属于自己子群的Ej，只有TC知道这个密钥.若想解得Ej，有两个可能途径：一是通过这一等式，求出的值，这将面临离散对数问题；二是通过直接计算求得，那必须得子群中所有的成员坦诚出自己所掌握的秘密xi与mi（从部分签名发送到DC的过程中可知mi并非严格保密，但不影响以下的分析），这样的合谋是毫无意义的，因为泄露自己的私秘密不能得到群以外的秘密.

（3）群私钥E的获取也必须通过解决离散对数问题或是整个群内成员的秘密坦诚才能成功，因此个人私钥xi，子群密钥Ej及群私钥E都难以得到.

（4）该方案可抵抗合谋攻击，因为在初始化条件中，我们设置了n＜2t，而签名是以子群为单位的，若要伪造签名并嫁祸给他人，则在某一子群中个人间的合谋泄密行为，在接下来的伪造过程中，至少一人会在其他的子群签名中会反而害到自己，所以，首先这是一种情理上的不可能性.且由（3）可知，因为各种私钥的难解性，伪造也不可能.另外，由文献［6］4.1中2）的分析可知，本方案也是不能伪造部分签名的.

由上可知，改进的方案可以抵抗第二部分所提出的一切攻击，所以改进的方案是安全的.

4 结束语

本文对XIE等人方案进行了合谋解密攻击和合谋伪造攻击，表明该方案是不安全的，任意t人与DC合谋即可生成一个有效的门限签名并嫁祸给他人，任意少于t人联合DC也可生成一个有效的门限签名.本文给出了一个改进方案，弥补了原方案的安全性缺陷.

［1］Desmedt Y，Frankel Y.Shared Generation of Authenticators and Signatures［C］／／Advances in Cryptology-Crypto'91.Berlin：Springer-Verlag，1992：457-469.

［2］费如纯，王丽娜，于戈.基于离散对数和二次剩余的门限数字签名体制［J］.通信学报，2002，5（23）：65-69.

［3］蒋瀚，徐秋亮，周永彬.基于RSA密码体制的门限代理签名［J］.计算机学报，2007，2（30）：241-247.

［4］彭庆军.一种基于椭圆曲线的可验证门限签名方案［J］.通信技术，2008，3（41）：104-106.

［5］朱培栋，姚谛，赵建强，等.基于秘密分享的安全组通信协议设计与实现［J］.计算机工程与应用，2007，43（30）：116-119.

［6］Xie Qi，Shen Zhonghua，Yu Xiuyuan.Threshold Signature Scheme Based on Modular Secret Sharing［C］／／International Conference on Computational Intelligence and Security，Suzhou：IEEE Computer Society，2008：442-445.

［7］Jan J K，Tseng Y M，Chien H Y.A threshold signature scheme withstanding the conspiracy attack［J］.Communications of the Institute of Information and Computing Machinery，1999，2（3）：31-38.

［8］Xie Qi，Yu Xiuyuan.Improvement of WPL's（T，N）threshold signature scheme［C］／／Proceedings of 16thInternational Conference on Computer Communication，Beijing：ICCC，2004，9（2）：1032-1035.

［9］Asmuth C，Bloom J.A modular approach to key safeguarding［J］.IEEE Transactions on Information Theory，1983，29（2）：208-210.

［10］于秀源，薛昭雄.密码学与数论基础［M］.济南：山东科学技术出版社，1993：145-146.

［11］杨建喜，刘东.一种安全的门限群签名方案及椭圆曲线上的实现［J］.计算机工程与科学，2009，31（2）：17-19.

Cryptanalysis and Improvement of a Threshold Signature Scheme

CHU Jing-jing1，2，YU Xiu-yuan1
（1.College of Science，Hangzhou Normal University，Hangzhou 310036，China；2.College of Nursing，Hangzhou Normal University，Hangzhou 310036，China）

In 2008，Xie et al.proposed a new threshold signature scheme based on modular secret sharing，which means secret sharing can be achieved by Chinese remainder theorem.The paper indicated that their scheme is insecure.Any t signers who conspire with DC can forge a valid threshold signature and frame others，and any less than t individuals who conspire with DC also can forge a valid threshold signature.To overcome the security weakness，the paper provided a modified scheme.

threshold signature；secret sharing；modular secret sharing；collusion attack

11.3969／j.issn.1674-232X.2012.02.013

TP309 MSC2010：94A60

A

1674-232X（2012）02-0157-05

2010-11-19

国家自然科学基金项目（10671051）.

褚晶晶（1986—），女，硕士，主要从事数论及其应用研究.E-mail：cjj0814＠hotmail.com