某单机无穷大电力系统暂态稳定性分析仿真

2012-08-29许江博韩宏亮张双平

中国水能及电气化 2012年1期

许江博，韩宏亮，张双平

（1.中国葛洲坝集团电力有限责任公司，宜昌 443000；2.三峡电力职业学院，宜昌 443002；3.湖北超高压输变电公司直流运检中心，武汉 430050）

随着电力系统规模不断扩大，系统发生故障的影响也越来越大，尤其大区域联网背景下的电力系统故障将会给经济、社会造成重大经济损失，因此保证电力系统安全稳定运行是电力生产的首要任务。

电力系统是一个复杂的动态系统，一方面，它必须时刻保证可靠的电能质量；另一方面，它又处于不断的扰动之中，扰动发生的时间、地点、类型、严重程度均具有较大的随机性。当扰动发生后，一旦发生稳定性问题，系统可能会在几秒内发生严重后果。对于系统某一特定的稳定运行状态，以及对于某一特定的扰动，如果在扰动后系统能达到一个可以接受的稳定运行状态，则系统运行处于暂态稳定。在电力系统规划、设计等工作中都要进行大量的暂态稳定分析。通过暂态稳定分析，可以看到各种稳定措施的效果以及稳定控制的性能。因此，通过时域仿真来验证电力系统在某一状态时是否稳定，具有重要的理论和实际意义。

1 电力系统仿真算法设计

现代电力系统暂态稳定分析方法主要有时域仿真法、暂态能量函数法等方法。时域仿真法是通过求解描述故障发生前、故障期间以及故障切除后，电力系统运行状态的微分-代数方程组得到各发电机转子摇摆曲线，从而根据各发电机是否能够同步运行来判断系统的暂态稳定性。

基于发电机的经典模型和计及励磁调节作用的模型，本文给出了适用于时域仿真法的电力系统暂态分析的数学模型。为不失一般性，发电机采用三阶模型，考虑到快速励磁自动电压调节系统后电力系统中每台发电机的运行状态，可用下列微分方程组来表示：

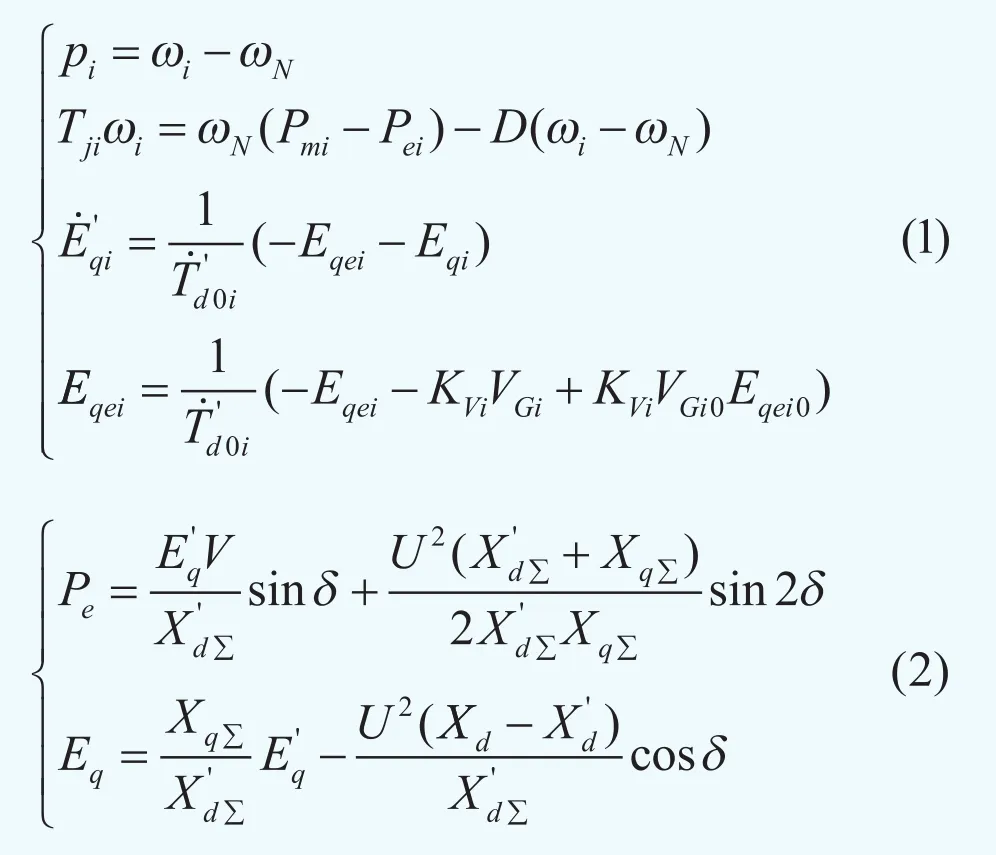
式中：

δi—发电机功角(rad)；

ωi—发电机转子角速度(rad/s)；

ωN—发电机转子额定角速度(rad/s)；

Tji—发电机转矩(N·m)；

D—发电机阻尼；

Pe—发电机有功出力(W)；

Eq—发电机q轴电动势分量(V)。

2 单机无穷大系统整体设计

为防止一些干扰影响到仿真中所得到的理想数据及波形，本论文选择了最具有代表性的典型的电力系统——单机无穷大系统。正常运行时，发电机经过变压器和双回输电线路向无穷大母线送电。该系统认为功率无穷大，频率恒定，电压恒定，即对现实进行近似处理，以简化模型，更有利于得出结论，简化计算过程。如图1所示。

图1 单机—无穷大系统简化模型

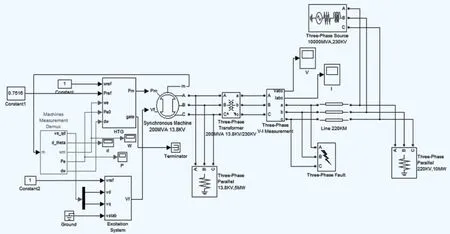
图2 单机无穷大系统仿真模型

图1 中，最左端是发电机组，Vt为机端电压，XT是变压器的电抗，XL1和XL2是线路电抗，Vs是无穷大电源电压。额定容量可根据仿真模型进行设定，额定电压Vt=13.8kV，额定频率fn=50Hz，变压器的变比k=13.8/230，无穷大电源电压Vs=220kV。

本文以上图1单机无穷大系统简化模型和上述公式(1) (2)为基础，采用Simulink中的Sim-Power-Systems相关模块来建所需要的系统模型，并进行故障分析。

3 单机无穷大系统暂态分析仿真

3.1 系统模型

根据公式(1) (2)以及上文分析可知，需要组成系统的几个主要部分分别是：发电机组、三相变压器、输电线路、负载、故障元件、测量仪器以及标准电压源。在进行发电机组的参数设置时，Rg，Vn，fn按照上述的额定值进行设置，转子类型（Rotor type）为凸极（Salient-Pole），其余相可用模块的默认值。三相变压器选择双绕组三相变压器（Three-Phase Transformer），将变比设置为13.8/230（高压侧额定电压为220kV），低压绕组三角形接法，高压绕组星型接地。另外，将标准电压源的容量设置成一个较大的值（本文设为10E10）来模拟无穷大系统。先用模块建立一个正常运行的电力系统，仿真后观察电压电流波形，待稳定后，再将故障元件加入其中，这样才能保证故障切除后系统最终能恢复到稳定状态，本文所研究的单机无穷大系统仿真建模图如图2所示。

3.2 仿真参数设置及潮流计算

短路故障是用三相故障元件来模拟的，在该模块的参数设置中选择A项以及接地故障，并将故障电阻Ron和接地电阻Rg都设为0.001。故障时间段可通过Transition times来安排故障起始时间和切除时间。其余模块的参数设置都要根据系统要求进行适当修改。由于电力系统是带发电机的刚性系统，因此算法ode15s，ode23tb适合采用，仿真停止时间设定为5s。

图3 t=0.9s时在阻尼D=0.1，D=0.8时发电机的功角曲线

图4 在忽略阻尼情况下，当t=0.8s，t=1s时发电机的功角曲线

图5 在阻尼D=1，t=0.7s时单相接地短路和两相短路接地时发电机的功角曲线

其余三种短路故障的模型与前面相同，唯一需要修改的地方则是三相故障元件的设置。对仿真参数设置为Start time（开始时间）选项为0；停止时间选项为Stop time ；5SType（求解程序类型）选项为variable-step(可变步长），ode23（stiff/TR-BDF2）； Max step size（最大步长）选项为1/60；Relative torlerance（相对容差）选项为1e-4；Absolute torlerance（绝对容差）选项为1e-3；其他采用默认值，电路发生两相短路接地故障。在进行潮流分配计算后，进行系统仿真。

4 仿真结果及分析

4.1 阻尼对仿真结果的影响

为研究阻尼D对仿真结果的影响，可将阻尼变为原来的8倍时即D=0.8在t=0.9s时切除故障，仿真结果如图3所示。

由上图3可知，D=0.1，t=0.9s时，系统已经失去稳定；D=0.8，t=0.9s时，系统仍然是稳定的。这是因为故障发生后，由于机械功率和电磁功率的不平衡，发电机转子角速度运动，使得第一摆有明显的震荡，随后角速度非常大，又由于有足够强的阻尼，再加上D·Δω的值很大，根据公式(1)可得：

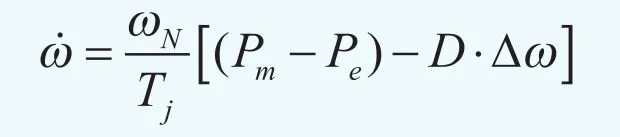
故此时系统处于减速状态，因此发电机的阻尼作用可以提高电力系统的暂态稳定性。

4.2 故障切除时间对仿真结果的影响

不考虑阻尼变化情况下的故障切除时间对仿真结果影响的仿真图如图4所示。

从上图4仿真结果可以看出，当t=0.8s时切除故障，系统是稳定的，这是因为随着时间的推移，发电机的功角δ和角速度ω发生持续周期性震荡；t=1s时切除故障，系统是不稳定的，这是因为随着时间的推移，发电机的功角δ和角速度ω发生非周期性的失步。在此种情况下，发电机的电磁功率P和端电压U发生大幅度的周期性震荡。如果不切除故障，则系统暂态不稳定；如果故障切除得较早，则系统稳定。可见系统的故障切除时间越长，系统越不容易稳定。