GPS／GLONASS组合定位的抗差Helmert方差分量估计模型＊

高 晓，戴吾蛟

（1.中南大学测绘与国土信息工程系，湖南 长沙410083；2.湖南省精密工程测量与形变灾害监测重点实验室，湖南 长沙410083）

0 引 言

GNSS定位的数学模型包含函数模型与随机模型，其中函数模型非常明确，且已得到广泛的认可，但由于GNSS的误差源较多，且通常与观测环境、仪器设备等有关，随机模型很难确定。GNSS随机模型可以分为两类：一类是根据反映观测值质量指标的高度角、信噪比等先验随机模型[1－3]；另一类是根据观测值残差进行验后估计[4]。在单个GNSS系统的动态定位中，由于多余观测较少，验后估计法不准确，常用于多余观测较多的静态定位中。随着GLONASS的复苏，GPS／GLONASS组合定位的研究与应用得到了进一步深入与发展，有学者已开始利用方差分量估计的方法精化随机模型[5－6]。已有研究表明，在 Helmert方差分量估计中引入抗差模型，建立抗差Helmert方差估计模型可以有效抵御粗差对方差估计的影响[7－9]，并成功应用于重力网平差计算、卫星精密定轨等领域中。利用高度角及抗差Helmert方差分量估计方法建立GPS／GLONASS组合伪距动态定位的随机模型，通过对IGS站（bjfs）2011年4月1日24h的观测数据进行计算分析，以检验方法的有效性。

1 抗差Helmert方差分量估计模型

对于来自不同系统观测值的组合定位，可以根据验前估计权进行预平差，用平差后得到的观测值改正数来估计不同系统观测值的单位权方差，如此重复，直到不同系统观测值的权趋于合理，这种平差方法称为验后方差分量估计。

2.1 Helmert方差分量估计模型

直接给出严密Helmert方差估计公式[9]：

2.2 基于IGGIII模型的抗差Helmert方差分量估计模型

Helmert方差分量估计可以较好地实现多类或多种精度观测值一并平差时的定权问题，但是当观测值包含粗差时，粗差产生的影响会转移到随机模型中，方差分量估计方法就会出现失真现象[9]。鉴于此，学者们提出了抗差模型，其实质就是赋予粗差数据较小的权重，削弱或者杜绝粗差的影响，解算出干净准确的数据。

设P为对角权阵，pj为第j项权值，则对应的抗差权重为：＝rjpj，式中，rj为自适应降权因子，与之对应的降权函数有IGGIII、Huber、Hampel等。采用IGGIII模型如下[10]：

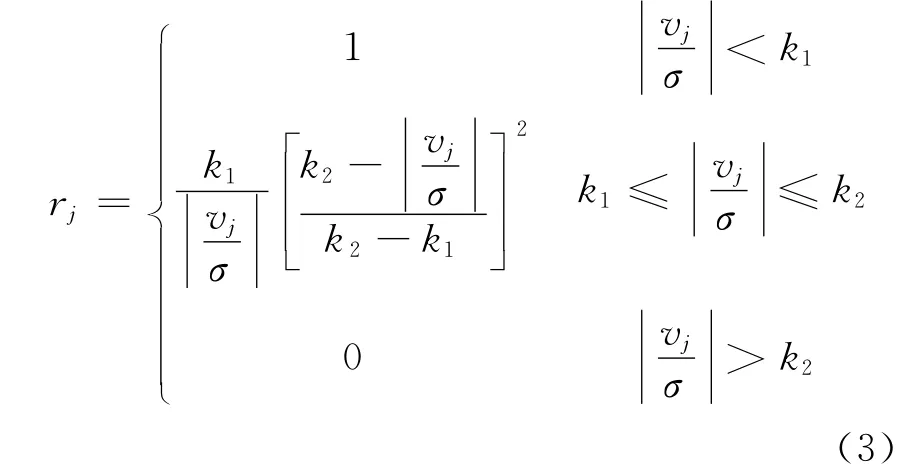
式中，k1、k2为常数，参照文献[10]，k1＝1.5～2.5，k2＝2.5～8.5.这里，k1与k2分别取值2.5与8.5.σ为方差因子，当迭代稳定后，方差因子的取值可采用：

2.3 抗差Helmert方差分量估计算法流程

1）将观测值按照不同类别分类进行验前定权，即确定各类观测值的初始权。按照高度角模型进行权阵的初始化：，其中a、b、σ的数值依据观测值来源的不同按照经验值进行设定，e为观测历元高度角；

2）确定设计矩阵后按照经典平差方法进行初次求解，求得V的初次估值；

3）取得残差序列后按照式（1）计算各类观测值方差因子的估值；

4）根据各类观测值方差因子估值重新定权并按照式（3）构建抗差权阵。式（3）的σ在迭代还未稳定时取第三步所计算的各类观测值的方差因子；

5）利用抗差权阵再次进行经典平差计算，求得V的平差值。重复上述步骤直至迭代稳定。若出现矩阵求逆0值溢出时（如高斯全主元消去法）时，适当放大方差因子；

6）待迭代稳定后，式（3）中的σ通过式（4）确定，完成后续迭代工作，直到改正数小于指定数量级。

3 算例分析

3.1 实验数据

实验数据取自IGS站北京房山（bjfs）站2011年4月1日24h的观测数据。数据文件包括GPS与GLONASS的混合观测值，采样间隔为30s，共计2 880个观测历元。2011年4月1日当天GPS卫星与GLONASS卫星的PDOP值如图1所示。当天GPS卫星与GLONASS卫星分布较好（最大值为2.5，最小值为1.1，均值为1.5），各时段PDOP值均在标定值（4.0）限定范围内，各观测时段没有异常状况发生。

图1 GPS／GLONASS卫星PDOP值分时统计图

同时，对当天GPS／GLONASS卫星数进行统计分析，卫星数最少为10颗，最多为21颗，平均为15颗，完全可以满足伪距单点定位对观测数据的数量要求。

3.2 解算结果

实验采用组合系统观测数据与导航电文进行单历元单点定位，将解算结果与ITRF2005参考框架下北京房山（bjfs）站的空间直角坐标进行对比，得到各历元的的坐标向量差及其RMS值如表1所示，其中Y方向的坐标残差序列如图2所示。

表1 不同定权方案定位结果对比

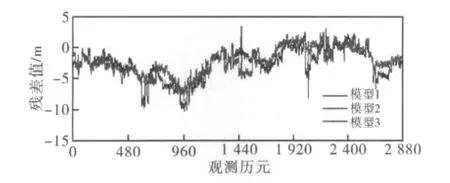
图2 Y坐标残差序列图

从表1和图2的结果可以看出：与传统的高度角模型对比，Helmert方差分量估计模型取得了较好的解算结果（Y 残差上限为2.335 3，下限为－8.474 3，均值为－2.398 6，STD为2.128 6），单点定位的精度也得到了明显提高。从Helmert方差分量估计模型衍生出来的抗差Helmert方差分量估计模型较单纯的Helmert方差分量估计模型在整体的平差结果来看又有所进步，曲线更加平滑，定位精度得到提高，各历元的RMS值也有所降低。

对于该IGS站的观测数据，采用Helmert方差分量估计模型进行平差解算，求取每个历元GLONSASS与GPS两类观测值的权比。2 880个历元的权比的均值为0.232 0，由此可知，GLONASS系统的精度明显偏低。但由于GLONASS采用频分多址技术，可以较好地抵制多路径效应的影响，在测量环境较差的测站可以发挥独到的优势，而且组合定位时可以大大增加观测值数据量，改善卫星图形分布强度，因此只要合理定权，组合定位可以提高定位的精度和可靠性。每个历元的权比如图3所示，从中可以看出，各历元的GLONSASS与GPS两类观测值权比并不是固定不变，而且有时差异较大。因此，进行组合定位时，GLONSASS与GPS观测值的权比取一个固定值是不合适的。

图3 观测值权比序列

高度角模型与Helmert方差分量估计最大的弱点就是无法抵御粗差观测值的影响，而抗差Helmert方差分量估计模型的最显著的优势就是具备良好的抗差性。为了体现这一特性，在原始数据随机地选取了10个历元的数据对GPS 2号卫星的伪距观测值添加＋50m的粗差，之后分别用三种随机模型进行平差计算，对比分析各历元数据计算结果，发现由于随机模型的不同，添加粗差后数据解算结果与ITRF2005框架下bjfs站坐标值的差值有所差异，坐标残差统计如表2所示，其中X、Y、Z方向的坐标残差序列如图4所示。

从表2和图4可以看出：当观测值中含有粗差时，高度角模型已无法保证定位的精度，单点定位结果存在较大的误差。同样，由于粗差的影响，Helmert方差分量估计模型同样受到了影响，出现了方差因子估计失真的现象，单点定位的精度也受到了影响，而且有时还会出现负方差的现象。而抗差Helmert方差估计模型则显示出较强的抵抗粗差的能力，即使观测数据中出现粗差，单点定位结果的坐标残差序列比较平滑，没有较大的波动。但是加入粗差的10个历元中，仍然有三个历元的坐标残差偏大。经过对这三个历元的残差进行全面分析，发现其中有3颗GLONASS卫星的观测值存在较大的误差（未加入粗差时，这三颗卫星观测值的残差大于3m）。这是由于观测数据的污染率较大，使得抗差效果降低了。

表2 添加粗差后的数据计算结果对比

图4 添加粗差后坐标残差序列（单位：米）

4 结 论

由于GNSS的误差源较多，且GLONASS与GPS存在系统差异，难以根据先验信息准确地确定GLONASS与GPS观测值的随机模型。采用Helmert方差分量估计方法可以根据实际观测值的精度动态确定GLONASS与GPS观测值的权比，但当观测值存在粗差时，该方法会出现迭代不收敛、负方差或方差估计失真的问题。基于IGGIII模型的抗差Helmert方差分量估计方法不仅可以动态确定GLONASS与GPS观测值的权比，而且可以有效抵御粗差的影响，同时由于自适应降权因子的作用，还可以根据平差后的残差调整单个系统中的高度角随机模型，使之更准确合理；但是，当观测值出现多个粗差时，污染率偏高，抗差效果会有所降低。

[1]戴吾蛟，丁晓利，朱建军.基于观测值质量指标的GPS观测量随机模型分析[J].武汉大学学报·信息科学版，2008，33（7）：718－721.

[2]GERDAN G P.A Comparision of four methods of weighting double－difference pseudo－range measurements[J].Trans.Tasman Surv，1995（1）：60－66.

[3]BRUNNER F K，HARTINGER K H，TROYER L.GPS signal diffraction modeling：the stochastic SIGMA－Δmodel[J].Journal of Geodesy，1997（73）：259－267.

[4]WANG J，SATIRAPOD C，RIZOS C.Stochastic assessment of GPS carrier phase measurements for precise static relative positioning [J].Journal of Geodesy，2002（76）：95－104.

[5]胡国荣，崔伟宏.组合GPS／GLONASS精密定位的观测值随机模型[J].遥感学报，2001，5（2）：95－99.

[6]段举举，沈云中.基于方差分量估计的GPS／GLONASS组合点定位[J]，测绘通报，2011（4）：4－6.

[7]康开轩，邢灿飞，李 辉，等，抗差 Helmert方差分量估计在重力网平差中的应用[J].大地测量与地球动力学，2008，28（5）：115－119.

[8]秦显平，杨元喜.抗差分量估计在卫星定轨中的应用[J].大地测量与地球动力学，2003，23（4）：40－43.

[9]刘长建，马高峰.抗差Helmert方差分量估计及其应用[J].北京测绘，2002（1）：16－18.

[10]徐天河，杨元喜.VLBI、SLR、GPS综合数据处理与坐标转换若干问题研究[D].测绘工程，2002，11（4）：7－11.