异步电机定子模态分析及定转子槽配合对其噪声的影响

管 兵(安徽皖南电机股份有限公司，泾县 242500)

0 引言

随着现代生活的发展，噪声的影响越来越受到重视，而电机是产生环境噪声的主要因素之一，因此降低电机的噪声成为重要的研究课题。异步电机的电磁噪声是噪声的主要组成部分，它不仅影响电机的可靠性运行，而且很大程度上影响人们的日常生活。预测电机的噪声，需要考虑定转子两方面的因素，研究电机定子模态以及定转子槽配合具有很重要的理论意义和实用价值。

国内外的专家学者对各类电机的噪声和振动问题，进行了较广泛的研究。文献［1-2］研究了大型异步电机的结构振动频率特性，以及绕组等部分对其固有频率的影响，文献［3-4］研究了中小型电机固有频率的计算，文献［5］研究了开关磁阻电机的定子模态和固有频率，文献［6］研究了超声波电机振动模态有限元分析，文献［7］研究了利用有限元方法(Finete Element Method，FEM)计算异步电机定子的固有频率。

本文针对某异步电机，利用ANSYS软件对电机的定子结构建立模型进行分析，以及通过公式计算电机定子的固有频率，并将两者比较;同时分析定转子槽配合对电机噪声的影响。为抑制电机噪声提供了理论依据，为异步电机的技术进步提供一定的参考价值。

1 异步电机定子的模态分析

1.1 定子冲片模态计算分析

多年来，在计算定子固有频率的理论公式［8］中，都存在不同程度的不足，没有较为准确全面的定子模态分析计算方法。在模态分析的过程中，可以忽略定子绕组对定子固有频率的影响。要考虑包括机座、外壳在内的影响因素，因为异步电机定子铁心都压入机壳中，增加了定子铁心的质量和刚度。很多文献针对异步电机的定子、转子、外壳等分别进行分析研究，得出不同的定子模态频率。

本文考虑外壳对固有频率的影响，假设定子铁心与外壳的刚度并联，则总的刚度、质量分别为其刚度和质量相加，其定子铁心的固有频率计算公式为［9］

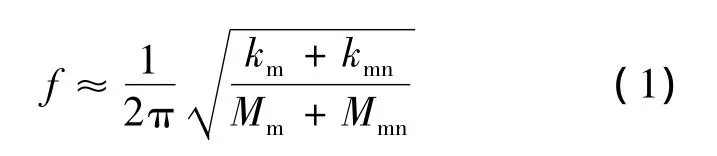
式中:km，kmn，Mm，Mmn分别代表定子铁心刚度，定子外壳刚度，定子铁心质量和定子外壳质量。

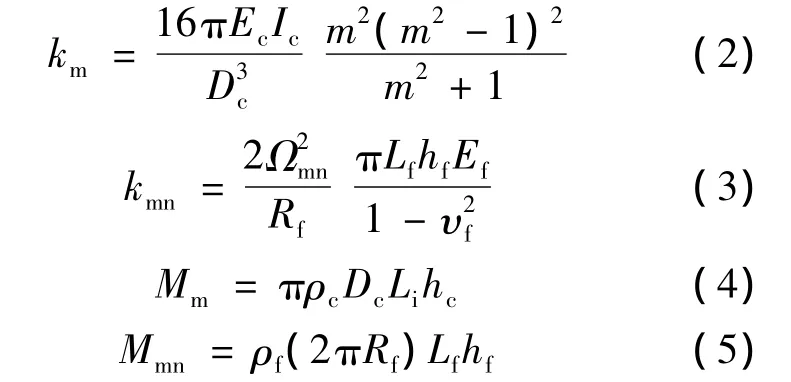
式中:Ec——定子铁心材料的弹性模量;

Dc——定子铁心平均直径;

Li——定子冲片长度;

hc——定子轭厚;

m——力波周向结点数;

ρc——定子铁心的材料密度。

式中:Ef——外壳材料的弹性模量;

Rf——外壳平均半径;

Lf——外壳轴向长度;

hc——定子轭厚;

Ωmn——表示无量纲的频率参数;

νf——泊松比;

ρf——外壳材料密度。

1.2 定子冲片模态仿真分析

在定子模态分析中，固有频率的计算一般可认为是无阻尼自由振动。电机结构的运动方程式可以写成:

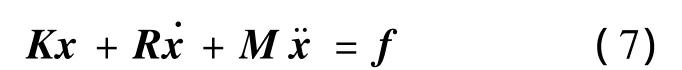
式中:K——刚度矩阵;

M——质量矩阵;

R——阻尼矩阵;

x——节点的位移矢量;

f——节点力矢量。

在电机的定子振动中，电磁力作用在定子铁心表面产生振动与噪声。定子振动中以径向振动为主，而且定子铁心具有各向同性特性，所以对定子冲片采用ANSYS［10］的二维模态分析方法。

电机主要受到作用于定子上的电磁力的激励，产生了噪声和振动，并且以径向振动为主，因此对电机定子冲片采用二维模态分析，能够反映电机的振动模型。

电机定子铁心48槽，转子44槽，定子冲片外径 290 mm，内径 205 mm，槽高 25.5 mm，槽宽6.5 mm。冲片材料采用硅钢50w290，其弹性模量E=2.061 ×1011Pa，泊松比PRXY=NUXY=0.3，密度为ρ=7 650 kg/m3。

建立定子冲片有限元模型，如图1所示。

图1 定子铁心三维模型

ANSYS计算所得的频率结果如表1所示。在电机设计中，根据计算公式计算［2］得到的频率也列于表1中，两者前10阶的模态分析比较可以看出振型的阶数是相似的，但频率有所差异。定子冲片的1～6阶谐振频率相应的振型如图2～图7所示。

图2 n=1

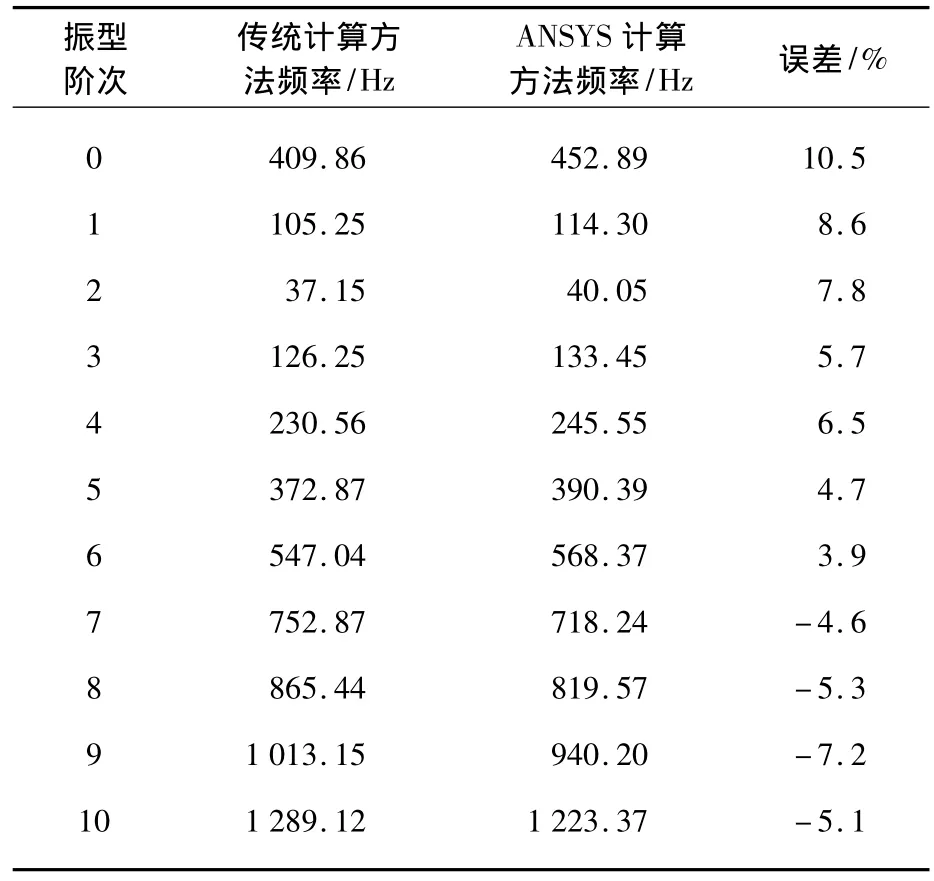
表1 定子冲片模态分析结果比较

由表1可以看出，定子冲片的模态计算与ANSYS计算方法误差较小。只有振型阶次与力波次数相同，且固有频率与力波频率相等时才会引起共振。

2 定转子槽配合及电流频率对电磁噪声的影响分析

电机转子如图8所示。转子槽形对称，绕组均匀分布，其目的在于能够在很大程度上消除电机运行过程中的谐波，增加气隙磁密。在此只考虑由于转子产生的谐波对气隙磁场的影响，进而影响电机整体噪声。

图8 转子冲片的模型

当定、转子都有齿槽时，气隙磁导可近似表示为

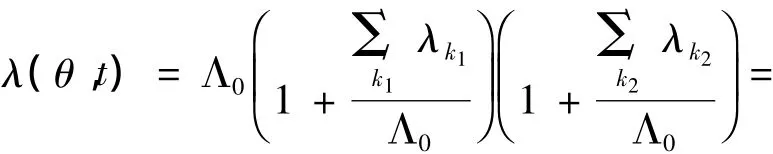
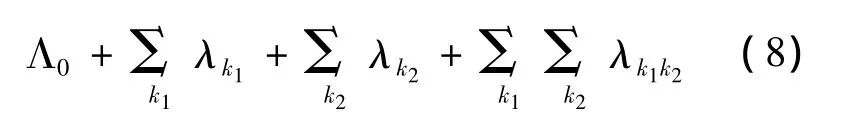
式中:k1=1，2，3……;

k2=1，2，3……。

磁导的不变部分是

式中:μ0——真空磁导率;

δ——气隙;

kc——卡特系数。

定子光滑，而转子开槽时，其谐波磁导:

式中:Z2——转子槽数;

ω——转子角速度;

p——极对数;

S——转差率。

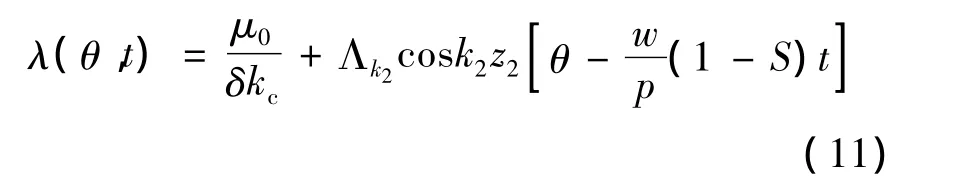
由于转子产生的磁势:

式中:Fμ——μ次谐波产生的磁势幅值。基波磁势为

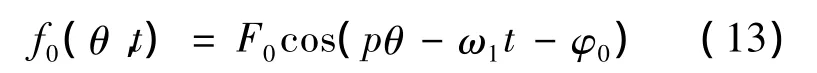
式中:F0——基波产生的磁势幅值。由此可看出气隙磁场为

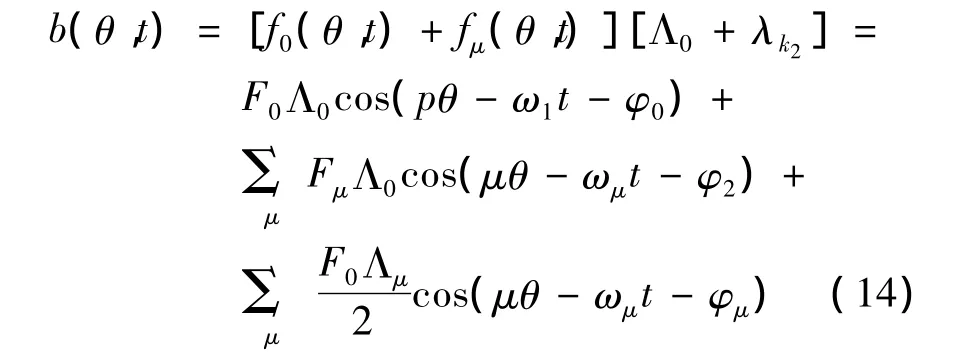
进而得到力波的表达式，最终得到电机辐射声功率的噪声级。

电磁力波引起的振动和噪声一方面与力波的幅值大小有关，另一方面还与力波的次数有关。次数越低铁心弯曲变形时相邻两节点间的距离就越大，因此变形就越大，所引起的振动和噪声也越大。一阶定转子齿谐波磁场所产生的激振力波的频率决定于转子槽数，而力波的低阶次数r则取决于定转子的槽数差，即

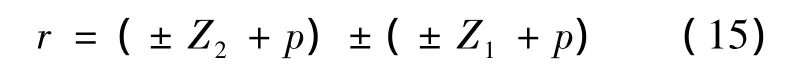
式(15)说明力波的次数与电机定转子槽数配合有关。若定转子槽配合不当，会使力波次数r较低，而可能产生较大的电磁振动和噪声。

同时可以看出，电机噪声与电源的频率有关。

通常按以下公式计算力波:

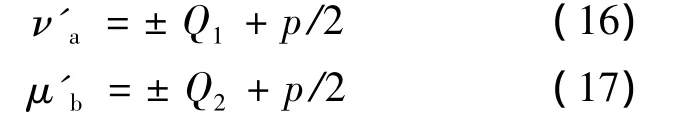
对正向力波:

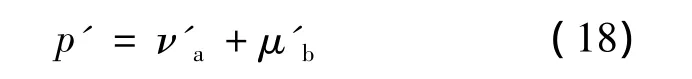
或者:

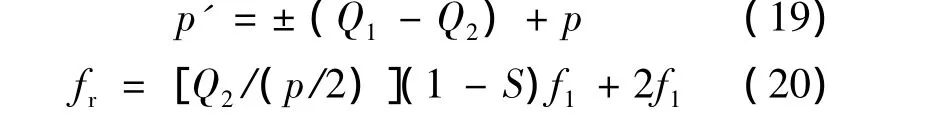
对反向力波:

或者:

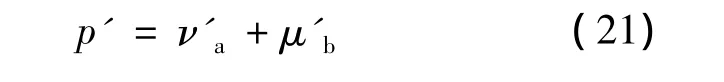
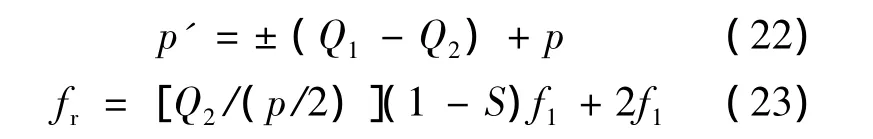
式中:ν'a——定子齿谐波次数;

μ'b——转子齿谐波次数;

p'——力波极对数，取最小值，p'=0，1，2，3，4……;

fr——力波频率;

f1——电源频率;

Q1——定子槽数;

Q2——转子槽数;

p——电机极数;

S——转子转差率。

按上述公式计算的力波极对数为最小力波，即为该电机电磁噪声频谱中最大噪声成分的激振力波。由此可决定力波方向，极对数和频率。

3 试验数据

在对电机进行测试时，将电机安放在半消音室测试平台上，上部悬挂一个半球状的测声装置，对电机各个测试点进行测试，求得其平均声压级。针对相同定子不同转子槽数的电机，其中一个为44槽转子的电机，另一个为38槽转子的电机，测得其声压级，进而分析转子槽数对其噪声级的影响。试验结果给出了不同测点及50/60 Hz下的噪声值。

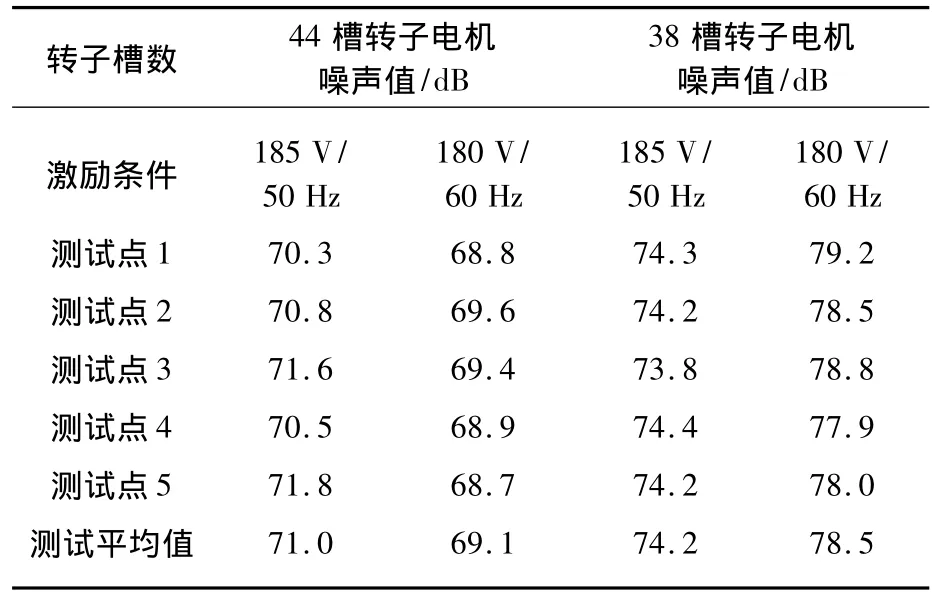
表2 不同转子槽数的噪声级对比

由表2可看出，不同的转子槽数可以影响电机的整体噪声级。其中44槽转子的电机比38槽转子电机的噪声级低，说明在相同定子下，44槽转子与其定子在槽配合上比38槽的噪声级更低，不同槽配合下电源频率对噪声影响较大。

4 结语

针对异步电机的噪声，利用软件及试验方法，分别分析定转子对噪声的影响。得出结论:

(1)在电机产生共振的频率段内会产生较大的噪声，所以在电机的设计过程中，尽量避免定子固有频率与力波频率相近的频段。通过定子模态分析，可以得到其固有频率和模态数。通过其与力波频率及力波阶次的比较，可以有效避免电机共振的发生。

(2)不同的转子槽数会导致电机整体噪声级的不同。在相同定子情况下，44槽转子的电机比38槽转子电机的噪声级低，不同槽配合下电源频率对噪声影响较大。

［1］王天煜，王凤翔.大型异步电动机定子振动与模态分析［J］.中国电机工程学报，2007，27(12):41-45.

［2］王天煜，王凤翔，白浩然，等.大型异步电机结构振动特性的研究［J］.机械强度，2009，31(1):140-143.

［3］王焕，宋正和.中小型异步电动机振动频率计算［J］.中小型电机，2004，31(6):15-18.

［4］ISHIBASHIF， KAMIMOTO K， HAYASHIT.Natural frequency of stator core of small induction motor［J］.IEE Proc on Electrical Power Application，2003，150(2):210-214.

［5］吴建华.基于物理模型开关磁阻电机定子模态和固有频率的研究［J］.中国电机工程学报，2003，24(8):110-114.

［6］莫岳平，胡敏强，徐志科等.超声波电机振动模态有限元分析［J］.中国电机工程学报，2002，22(11):92-96.

［7］余渊.ANSYS软件在交流电机定子振动研究中的应用［J］.上海大中型电机，2002(4):21-26.

［8］陈永校，诸自强，应善成.电机噪声的分析和控制［M］.浙江:浙江大学出版社，1987.

［9］JACEK F G，CHONG W，JOSEPH C L.Noise of polyphase electric motors［M］.Boca Raton:CRC Press，2006.

［10］博嘉科技.有限元分析软件—ANSYS融会与贯通［M］.北京:中国水利水电出版社，2002.