永磁电机分析的场路耦合时步有限元法

梅 凡， 谢宝昌， 高 强， 蔡 旭，2

(1.风力发电研究中心，上海交通大学电子信息与电气工程学院，上海 200240;

2.海洋工程国家重点实验室，上海交通大学船舶海洋与建筑工程学院，上海 200240)

0 引言

在自起动永磁同步电机中，气隙中的磁场会由于绕组分布以及定转子开槽等原因而发生畸变，从而影响电机的运行特性。电流会产生高强度的谐波分量，电磁转矩出现一定的脉动，振动噪声和谐波损耗等干扰也会随之产生，会降低电机的效率，给系统运行的稳定性带来危害。在传统的基于d、q轴的理论分析中，往往忽略电流的高次谐波分量，这会给永磁电机的电磁场计算和性能分析带来一定的误差。可以采用场路耦合的模型来解决此问题，并结合有限元的方法，使计算和分析的结果更加精确。首先建立好定转子回路的电路方程和电机模型各个区域的电磁场方程，再将电磁场有限元方程与瞬态定转子电路方程联立起来，这样就能够解出每个瞬时时刻对应的定子相电流和电机的电磁转矩。采取此方法，经过傅里叶分析可得到各次谐波分量，这样使计算结果更能模拟永磁同步电机的实际运行情况，分析更具有实际的应用意义。

文献［1］采用场路耦合时步有限元法分析永磁电机时，并未将转子电路方程与电磁场方程耦合。本文考虑转子导条时采用异步电机的鼠笼条的等效方法，给自起动永磁同步电机建立了较为完整的场路耦合模型。首先建立了永磁电机的定转子电路方程和电磁场方程，然后再将它们耦合。在实际仿真运行时，采用气隙边界运动法来模拟转子的运动，并给出具体的计算和求解过程。最后对一台2.2 kW的自起动永磁同步电机采用场路耦合的方法进行了有限元仿真，分析其电磁场及运行特性。

1 电机的定转子方程和电磁场稳态方程

1.1 电机的定转子电路方程

永磁电机定子绕组的等效电路图如图1所示。

图1 定子绕组等效电路图

为了更加精确地计算电机的参数，在定子电路方程中，要将定子的端部效应计入其中。同时，谐波分量带来的影响以谐波漏抗的形式反应到定子漏电感当中去。各个线圈按照一定的串并联的连接方式并分相后构成各相绕组，接到电源上。以电压为输入量，列写定子绕组各相的回路方程:

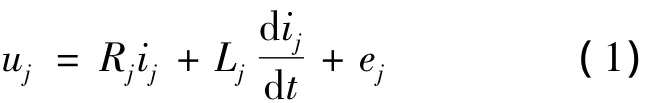
其中:下标j=a，b，c;

uj——各相的输入电压;

ij——每相绕组的定子电流值;

Rj——定子各相绕组的等效电阻，与导体材料的用量和连接方式有关;

Lj——各相的漏电感，包括槽漏电感，端部漏电感，谐波漏电感等;

ej——各相绕组的反电势。

在分析永磁电机的稳态运行且仅考虑磁场基波分量的情况下，转子导条中的感应电流可忽略不计。这是因为在稳态情况下，转子以同步速旋转，转子与电源产生的旋转磁场之间无相对运动，所以鼠笼条中也就没有感应涡流。但是为了分析高次谐波磁场的作用，就必须考虑转子导条中的

式中:uk——转子第k个导条上的电压;

ik——第k个导条上流过的电流;

Re——两相邻导条间的端环的等效电阻;

Le——等效电感;

iek——流经第k个和第k+1个导条之间的端环的电流。

1.2 电机电磁场的稳态分析模型

忽略定、转子铁心中的涡流及转轴方向上的磁场变化，计及转子导条的感应涡流。各个区域的电磁场方程如下。

1.2.1 无外加电流区域

在这个区域包括定转子铁心部分，气隙部分及永磁体部分。永磁体用面电流模拟，体现为边界的面电流密度，其余部分电流密度为零。所以该区域的电磁场方程为电流，因为电源产生的高次谐波的转速不等于同步速，转子导条与高次谐波产生的磁场之间有相对运动，就产生了感应电动势，从而形成感应电流。

转子导条的电流回路和电压平衡方程式为

1.2.2 定子绕组区域

定子绕组由线圈组成，线圈中流有电流，该部分的方程为

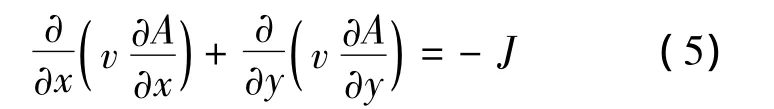
式中:N1为一个线圈的匝数，α为并联支路数，Sb为线圈一个边所占面积，αi(i=a，b，c)为单元绕组电流系数，且他们的值为

J为电流密度，且:

其中，i=A，B，C。可以看到，绕组电流系数的取值与该区域槽电流是否导通和电流的方向有关。

1.2.3 转子导条区域

转子导条部分的电磁场方程为

式中:Lef为导条有效长度，磁矢位和导条电压为未知量。

2 场路模型的耦合与有限元法计算

场路耦合法就是以三相电压源作为已知量输入，将用瞬时值表示的电机定、转子回路的电路方程与电机电磁场方程通过电枢绕组的感应电动势联立起来，并结合转子的机械运动方程，直接计算电机的磁矢位、绕组电流和电磁转矩等，运用电机瞬态电磁场的方法，精确分析电机从起动过程到稳态运行整个过程的运行性能。在每个求解时刻下，电机的电磁场近似按照稳态场来处理，电机的转速也假定不变，在求出此时刻电机运行的各项参数之后，根据机械运动方程，就可以得到下一求解时刻转子位置，从而开始下一个稳态时刻的求解。将这些稳态求解时刻的计算结果结合起来，就得到动态解。因此，只要计算的步长Δt选取得合理，计算结果就能完全模拟电机的实际运行情况。

利用场路耦合时步有限元法，可以将铁心饱和造成的磁路非线性，齿槽效应，端部效应，涡流效应等都考虑进去，并且能计算出漏磁系数、波形系数、漏电感、谐波损耗等初步设计不易计算的参数，从而使设计和分析更加精确和合理。

2.1 场路模型的耦合

定子绕组的感应电势是把定子区域场路耦合模型耦合起来的枢纽，这是因为每相的感应电势是绕组回路电压平衡方程式中的一项，但是它需要通过电磁场的计算来得到。反电势可以通过交链磁链的变化率求得，而磁链的值又与节点的磁矢位的大小有关。每相绕组的反电势为

式中:下标x=a，b，c;

Ψx——相绕组磁链;

Lef——绕组有效长度;

np——单元总数;

p——极对数。

在电磁场的方程中，定子绕组部分的电流和磁矢位，以及转子导条部分的电流和电压是未知量。采用差分来代替求导，运用加权余量法，取权函数等于形状函数。并将定转子的电磁场方程和电路方程进行耦合，得到整个电机的场路耦合方程:

其中第一行是电磁场方程，第二行是定子绕组电路方程，第三行是转子的回路电流方程式，第四行是转子的电压平衡方程。A表示矢量磁位，is表示定子绕组电流，u表示转子导条的电压，ir表示转子导条的电流。M表示永磁体的励磁作用，us表示定子绕组的电压。系数矩阵中的系数要通过单元分析和总体合成得到。

为了能够得到永磁同步电机的瞬态特性，计算电机的转速和每个时刻对应的转子轴线的机械角度，要将转子的机械运动方程与上述场路耦合方程相结合。机械运动方程为

可以在区域求和代替面积分。

2.2 转子运动的模拟

当模拟转子运动时，如果对每一个转子运动位置的情况重新建模，再划分网格进行求解，那将要耗费大量的时间，使得前处理太过复杂。可以采用气隙边界运动法解决此问题。将气隙部分沿着气隙中心线平均分成两部分，靠近定子侧的部分，位于定子区域的静止坐标系中，靠近转子侧的

其中电磁转矩的计算为部分，位于转子区域的旋转坐标系中。当转子旋转时，两部分的气隙相对于各自的坐标系都是静止的。只有两部分重合的边界，也就是气隙中心线是相对运动的。因此可以将气隙中心线沿圆周进行等距离的设置节点，这样当转子运动时，定子气隙部分的节点方程不变，只需要将转子气隙边界的节点编号进行旋转后的重新对位，列写方程即可。

2.3 求解过程

为了分析永磁电机的机电能量转换，要同时求解电机的电磁场方程和机械运动方程。计算过程如下:

(1)给定负载转矩，设定初始时刻的定子绕组三相电压，并设定求解的步长Δt。

(2)在每一个求解时刻t=t0+nΔt，利用场路耦合方法，求解电磁场有限元方程，直至收敛，得到此时的磁场分布，各个节点的电流的大小和磁矢位的值。

(3)计算气隙中心线上节点的电磁转矩，再根据转子的机械运动方程求出机械角速度Ωr的变化率，然后得到下一时刻的角速度和转子中心线的位置。

(4)反复执行(2)和(3)，直至仿真时间达到设定的终止时刻且电机已进入稳态运行，最终得到电机的暂态运行曲线。

3 场路耦合有限元法的仿真实例

本文以一台2.2 kW的永磁同步电机为例，先利用传统的等效磁路法对这台电机的尺寸大小，永磁体的结构，定、转子的槽型等进行了设计;然后通过场路耦合时步有限元法对设计好的电机进行仿真计算分析。

3.1 电机的基本结构和主要参数

利用等效磁路法所设计的永磁同步电机的基本参数如下:额定功率2.2 kW，额定电压380 V，极对数3，定子槽数27，转子槽数24，定子内径140 mm，铁心长度120 mm，气隙长度0.25 mm，其截面图如图2所示。

采用内置径向式的转子结构，结构简单，转子的机械强度高，有较强的安全性和可靠性。

为了永磁同步电机的自起动需要，并且能尽量减小反电势中的高次谐波，定子槽数采用分数槽，这样的设计也有利于减小齿槽转矩，同时为便

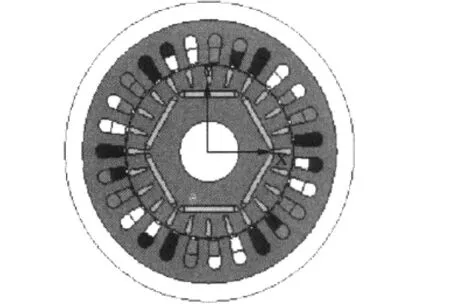
图2 永磁同步电机的截面图

于控制极弧系数，尽量满足转子磁路的对称性，并考虑极槽配合的情况下，选定转子槽数为极数的整数倍。因为是永磁体励磁，将绕组连接成星型，有利于减小杂散损耗，并且可以防止三次谐波在绕组之间产生环流。

3.2 空载电磁场分析

当没有外加的激励源，只有永磁体磁场的独立作用下，永磁同步电机的磁力线分布如图3所示。

图3 永磁同步电机空载时的磁力线分布

可以看到，大部分的磁力线都从永磁体的磁极出发，依次经过转子齿，气隙，定子齿，定子轭，然后再经过定子齿，气隙，转子齿，最后回到永磁体。这是因为铁磁材料的磁导率比绕组导体大得多，大量磁力线从铁心中流过，各部分磁力线分布合理。

静态情况下，还可以得到永磁同步电机的空载气隙磁密波形，如图4所示。由于是永磁励磁，所以气隙磁密波形近似矩形波，但是由于定转子开槽的影响，使得气隙磁阻不均匀，进入槽的磁力线比较稀疏，而进入铁心齿部的磁力线比较密集。

3.3 额定负载运行特性分析

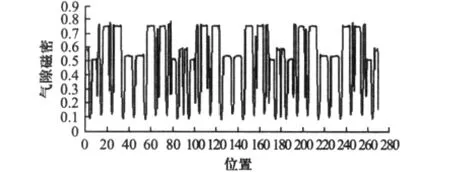
图4 空载气隙磁密

给永磁同步电机施加额定负载TN=20 N·m，联立机械运动方程和场路耦合方程，就能得到电机带负载起动的运行特性。电机的相电流、电磁转矩、机械角速度的相应曲线分别如图5～图7所示。

起动过程中，电磁转矩比较大，由转子导条提供，转子角速度曲线的坡度比较陡，加速度比较大，能较快牵入同步速。在t=0.4 s后，相电流基本为正弦波，电磁转矩等于负载转矩，有轻微的脉动，电机转速稳定在同步速。永磁同步电机进入稳定运行状态。

4 结语

本文利用场路耦合时步有限元法来分析永磁同步电机，并对一台2.2 kW的电机进行了二维电磁场的有限元仿真分析，得到了电机的磁场分布、相电流波形、转矩响应曲线和转速特性曲线，通过与实际值比较分析，验证了所建立的场路耦合模型的合理性。此方法在分析永磁电机时，考虑到了齿槽效应、绕组分布、铁心饱和引起的磁路非线性等问题，给永磁电机的设计和分析提供一个借鉴，同时对计算得到的电流和转矩进行傅里叶变换，可以得到各次谐波的分量，这给电机设计的优化提供了参考。因为是以定子端电压作为输入量，所以这种场路耦合时步有限元法不仅适用于三相正弦波供电的情况，也可应用在多相永磁电机，电压为逆变器供电等其他波形的情况。

［1］唐任远.现代永磁电机理论与设计［M］.北京:机械工业出版社，2007.

［2］FRANKLIN P W.A theoretical study of the three phase salient pole type generator with simultaneous AC and bridge rectified DC output［J］.IEEE Trans Power App Syst，2009，PAS-92(2):543-557.

［3］KATAOKA T，WATANABE E H，KITANO J.Dynamic control of a current-source inverter/doublewound synchronous machine system for AC power supply［J］.IEEE Trans Ind Applicat，1981(IA-17):314-320.

［4］STEWART J R，WILSON D D.High phase order transmission—a feasibility analysis，part Ⅰ—steady state considerations［J］.IEEE Trans PAS，1978，97(6):2300-2307.

［5］刘瑞芳.基于电磁场数值计算的永磁电机性能分析方法研究［D］.南京:东南大学，2002.