例谈抽象函数问题的『原型』解法

☉湖北省孝感高中 幸 芹

例谈抽象函数问题的『原型』解法

☉湖北省孝感高中 幸 芹

所谓抽象函数，是指没有明确给出函数表达式，只给出它具有的某些特征或性质，并用一种符号表示的函数.研究抽象函数问题的解法，对教师的教学以及学生深刻理解并牢固掌握函数的相关内容有较大的促进作用.

抽象函数是由特殊的、具体的函数抽象而得到的，如y=kx（k≠0）满足f（x+y）=f（x）+f（y），那么y=kx就可叫作抽象函数f（x）的“原型”函数.根据抽象函数的结构，联想到已学过的具有相同或相似结构的某类“原型”函数，并由“原型”函数的相关结论，预测、猜想抽象函数可能具有的某种性质使问题获解，我们称这种解决抽象函数问题的方法为“原型”解法.下面给出高中阶段几种常用的“原型”函数，并结合近几年全国各地的高考真题展现“原型”解法的实用性.

一、一次函数

若函数f（x）为R上的单调函数，且满足f（x+y）=f（x）+f（y）－b，则f（x）的原型函数为一次函数f（x）=kx+b（其中k和b为常数，k≠0）.

例1（2008年重庆卷）定义在R上的函数f（x）满足：对于任意的x1，x2∈R，总有f（x1+x2）=［f（x1）+f（x2）］+1，则下列说法正确的是（ ）.

A.f（x）为奇函数B.f（x）为偶函数

C.f（x+1）为奇函数D.f（x）+1为奇函数

解析：由条件，我们可猜测f（x）的原型函数为f（x）=x－1，故此题答案为C.

二、二次函数

若x∈R时，函数f（x）满足f（A+x）=f（A－x），则f（x）的原型函数为二次函数f（x）=k（x－A）2+B（其中A、B、k均为常数，k≠0）.

例2（2009年陕西卷）定义在R上的偶函数f（x）满足：对于任意的x1，x2∈（－∞，0］（x1≠x2），有（x2－x1）［f（x2）－f（x1）］＞0，则n∈N*时，有（）.

A.f（－n）＜f（n－1）＜f（n+1）

B.f（n－1）＜f（－n）＜f（n+1）

C.f（n+1）＜f（－n）＜f（n－1）

D.f（n+1）＜f（n－1）＜f（－n）

解析：此题中的f（x）为偶函数，并且在（－∞，0］上单调递增，则我们可以选择二次函数f（x）=－x2作为它的原型函数，故可得到f（n+1）＜f（－n）＜f（n－1），即可选C.

三、指数函数与对数函数

①若函数f（x）满足f（x+y）=f（x）·f（y），则f（x）的原型函数为指数函数f（x）=ax（a＞0，a≠1）.

②若x＞0时，函数f（x）满足f（x+y）=f（x）+f（y），则f（x）的原型函数为对数函数f（x）=logax（a＞0，a≠1）.

例3（2007年山东卷）给出下列三个等式：

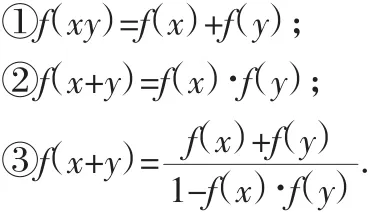
下列函数中不满足其中任何一个等式的是（ ）.

A.f（x）=3xB.f（x）=sinxC.f（x）=log2xD.f（x）=tanx

解析：分析题意可以发现，f（x）=log2x符合等式①，f（x）=3x符合等式②，由两角和的正切公式可知f（x）=tanx符合等式③，故选B.

四、三角函数

五、不拘一格，灵活多变

解决抽象函数的问题除运用以上所提到的四类常见的原型函数之外，我们还可以根据题目所给的具体条件，进行多种多样的探索和尝试.

抽象函数问题的“原型”解法，对选择题和填空题特别有效，可以迅速解决问题；对于解答题，也可起到提示思路和检验结果正确性的作用.我们在平时的学习过程中，要多总结、多反思、多探索，当有新的原型函数出现时要及时收藏，从而壮大自己能够灵活运用的原型函数的队伍，提高解决抽象函数问题的本领，促进数学学习的各种能力.

例4（2011届湖北省八校第一次联考）已知奇函数f（x）满足对任意的x∈R都有f（2+x）+f（2－x）=0，且f（1）=9，则f（2010）+f（2011）+f（2012）=________.

解析：由条件f（2+x）+f（2－x）=0可知函数f（x）的图像关于点

1.江战明，黄宗巧.让“模特儿”在抽象函数中合法代言.数学通讯（教师版），2010，5.

2.李振福.由2009年高考题窥视抽象函数考查的新动向.中学数学月刊，2009，10.

3.赵建新.一类“恒等式型”抽象函数问题的求解.中学数学杂志（高中版），2010，1.