“形”中的最值
2012-08-28江苏省姜堰市励才实验学校仇锦华
☉江苏省姜堰市励才实验学校 仇锦华
说到初中数学中的“最值”(最大值或最小值),往往会让人联想到从“数”的角度去建立函数关系式,求函数的最大值或最小值.而有时从“形”的角度去研究最值则显得更加直观、简洁.在几何中与“最短”、“最长”相关联的知识点有:“两点之间线段最短”、“垂线段最短”、“三角形两边之和大于第三边,两边之差小于第三边”等.

一、两点之间线段最短
例1 如图1,已知∠MON=90°,P、Q在两直角边上运动,且PQ=2,以PQ为边在PQ上方作等边△PAQ,求AO的最大值.
分析:A点是随P、Q的运动而变化的.虽然OA是动的,但我们要善于在“动”中寻“静”.因为PQ=2,即Rt△PQO的斜边,等边△APQ的边长不变.故取PQ中点D,则

小试牛刀:
如图2,菱形ABCD中,AB=2,∠ABC=60°,E为BC中点,P为BD上动点,求PE+PC的最小值.
提示:利用轴对称将PE+PC转化为PE+PA,因为PE+PA≥AE,所以最小值为AE的长.
二、垂线段最短

图3
例 2 如图3,Rt△ABC中,∠C=90°,P,Q在AC,BC上运动,且以PQ为直径的圆与AB相切,求PQ的最小值.
分析:在Rt△PQC中,以PQ为直径的圆必过C点,若将PQ看成是△PCQ的斜边,△PCQ其余两边PC,CQ都是变化的,不能求出PQ的最小值,若将PQ看成是圆的直径,则PQ长可以转化为两个半径之和.
解:设PQ中点为O,⊙O与AB相切于点H,则OH⊥AB,OH=所以PQ=CO+OH,根据“两点之间线段最短”,“垂线段最短”,可知当C,O,H共线且COH垂直于AB时CO+OH最短,即当CH=4.8时,PQ最小值为4.8.
提示:作N关于AD的轴对称点H,当B、M、H在一条直线上且BMH垂直于AC时最短.

图4
三、综合运用
例3 已知抛物线y=-x2+2x+3交x轴于A,B与y轴交于C,顶点为N,C,D关于对称轴对称,直线AD交y轴于E,P为线段DE上一点,自P作PH⊥y轴于H,求PH+PN最小值.
分析:此题若从数上考虑最值,则需设P点坐标,用P点的横坐标表示PH+PN,式子比较复杂,且含二次根号.若从形上考虑,则发现,A(-1,0),D(2,3),可知∠DAB=45°.若从A作直线AM⊥x轴,则P为∠MAB的角平分线上一点.PH+1=PG,所以PH+PN=PG+PN-1.
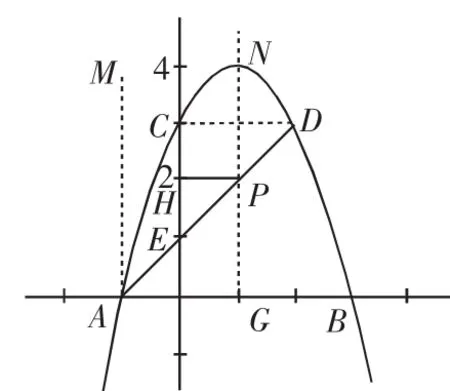
图5
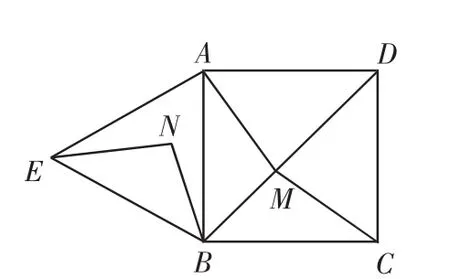
图6
解:自A作直线AM⊥x轴,自P作PG⊥AB于G,易得A(-1,0),D(2,3),N(1,4).
所以∠DAB=45°,所以PA平分∠MAB,所以PH+1=PG,所以PH+PN=PG+PN-1.
当N,P,G三点共线,且NG⊥x轴时PG+PN最小为4,所以PH+PN最小值为3.
小试牛刀:
如图6,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB.
(2)①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
