基于节点的既有雨水管网系统可靠度研究

赵子成，禹华谦

(1.西南交通大学土木工程学院，四川成都610031;2.中国中铁二院工程集团有限责任公司，四川 成都610031)

近年来，在极端天气和城市化的不断影响下，暴雨过程中，原本可以被洼地存贮、植物吸收或者直接渗入地下的雨水，因硬化地面阻隔并聚集成地面径流流入城市的雨水管道［1］，加之管道长期使用过程中腐蚀结垢、泥沙淤积，使得城市既有管网系统超过了设计时预期的排水能力，造成管网局部地面的积水、冒水等，从而引发城市内涝、交通瘫痪，严重妨碍了人们的正常生活和工作。因此，上述这些现象都对既有城市雨水管网的可靠性提出了更高的要求。

对于排水管网，国内外的一些学者在可靠性方面做了一定的研究分析。周玉文，等［2］运用可靠性理论作为分析根据，提出了基于排水管网可靠性的基本数学计算模型。张子贤［3］为阐明管道过水能力、水力因子的概率分布以及统计参数，提出了一种可靠性基础上的雨水管道水力设计方法。2006年，郭瑞，等［4］将结构可靠性理论应用到实际雨水管网，以雨水管道作为研究对象，给出了雨水管道系统目标可靠指标参考值，并提出了基于雨水管道的概率极限状态水力计算方法。笔者综合考虑节点与管段的关联关系，采用结构可靠度理论，从既有雨水管网系统节点出发研究，结合使用高精度的Monte-Carlo法确定节点处的可靠度，然后采用串联结构模型窄界限法确定出既有管网的可靠度。

1 节点可靠度不确定性的研究

设Qi，Qi+1分别为排水管网系统中任意节点M上、下游管段的流量，q为节点M汇入的暴雨流量，则事故节点M突降暴雨情况下的截余流量:

节点截余流量 QM，根据 Qi，Qi+1，q的关系，有3种情况，如式(2):

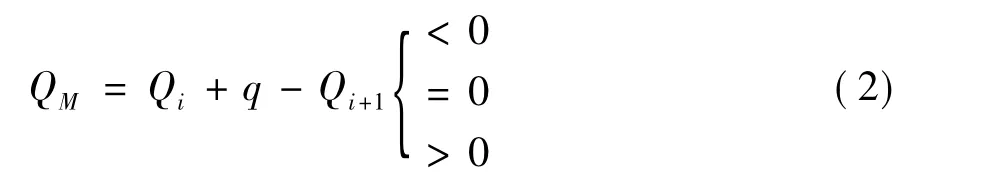
当QM＜0时，上游管道排水能力小于下游，系统节点运行正常;当QM=0时，节点处于临界状态，此时下游管道排水能力正好等于上游;当QM＞0时，说明上游管道排水能力超过下游，系统节点出现排水不畅，表现为上游管道出现回水，节点处水位高于管顶标高，下游管道重力流转化为压力流状态，节点出现超负荷运作。

根据结构可靠度概念［5］，任意节点M可靠度PS可以定义为:节点M上游管道的输水能力Qi与节点汇水流量QS小于等于节点下游管道的输水能力Qi+1的概率;任意节点M失效率Pf定义为:节点M上游管道的输水能力Qi与节点汇水流量QS大于节点下游管道的输水能力Qi+1的概率，即:

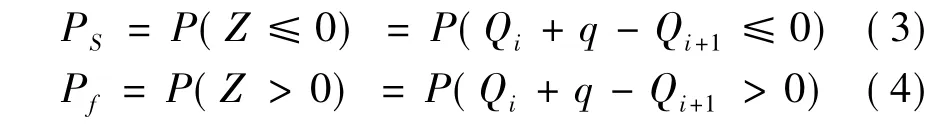
由式(3)可知，影响节点可靠度的因素为Qi，Qi+1以及节点处的汇水流量q。然而事实上，由于降雨条件，管材制造、施工、测量等误差以及管道长期使用的不确定性等，都会使式(3)具有一定的不确定性。因此，笔者从影响节点可靠度的各因素的不确定性入手，进行研究节点可靠度PS的研究。

1.1 基于管道输水能力的不确定性

设计条件下，雨水排水管道的通水能力Q按照满管无压均匀流考虑。由恒定流连续性方程、谢才公式［6］和曼宁公式可得管道通水能力为:

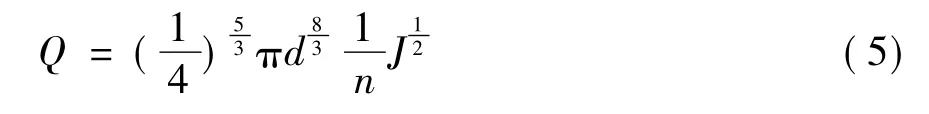
式中:d为圆管管径，m;J为水力坡度;n为管道粗糙系数。

管道实际流动时是非恒定、非均匀流的，而雨水管道设计时则是假定明渠恒定均匀流动。因此，使用计算公式时会产生计算模型的不确定性。

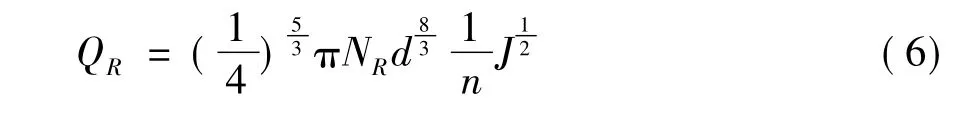
式中:NR为公式模型误差修正系数。

可见实际管段的通水能力与NR，d，J，n直接相关，都存在着不确定性，很难不出现超负荷工况。

1.1.1 排水管道d的不确定性

雨水管道d的不确定性来源主要包括两个［7］:①在制作过程引起的尺寸偏差以及安装过程造成的施工误差;②在使用过程中管壁引起结垢、泥沙造成淤积的不确定性。

1)制造偏差和安装偏差

管径制造的允许误差，安装偏差按照合格品计算，由此便可确定出各管径的变化范围，在变化范围内采用均匀分布。管道制作过程中管径d的通用市政管道制作偏差［8］如下:公称直径300～900 mm的管道合格品允许误差为±6 mm，而1 000～1 500 mm的管道则为±8 mm。

2)淤积和管壁结垢

在排水管网使用过程中，泥沙淤积和管壁结垢，以及管道是否定期清通与养护也会对管道的有效管径d产生相当大的影响。管壁结垢对过水面积影响很小，这里不考虑，归结于粗糙系数n的不确定性上面。如图1，假设h为管道泥沙厚度，均匀淤积在管底。考虑管道满流为最不利情况，则其过水断面面积为:

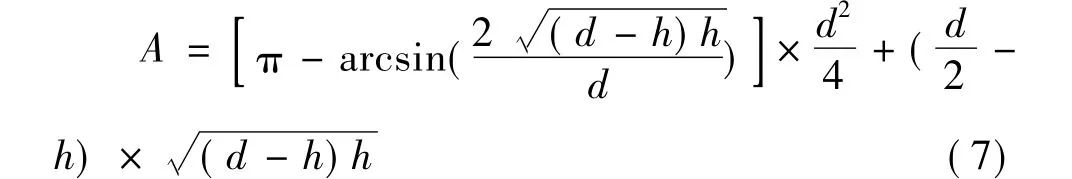
湿周为:

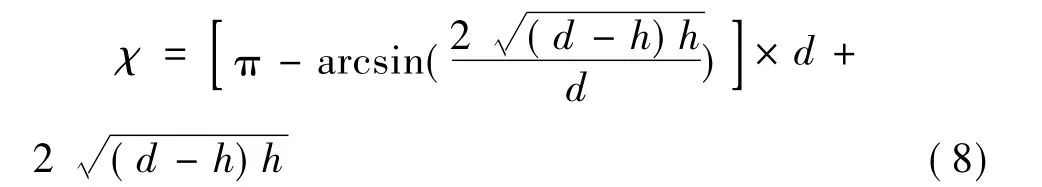
有效管径为:

式中:R为水力半径，m。

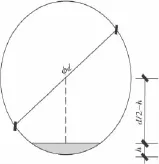
图1 既有管道过流能力计算示意Fig.1 Calculation diagram of the flow capacity of the existing pipelines

因为管内泥沙具有随机性，养护时会定期疏通，假设h的厚度不会超过管径d的1/10，取值在变化范围内假设服从均匀分布，经计算泥沙造成的有效根据范围为(0.961 27～1)d。综上，由统计参数的均匀分布可得平均值d、变异系数 δd和标准差 σd。

1.1.2 粗糙系数n的不确定性

管材质量、管道尺寸、管底沉积物、管壁结垢物和与管道表面内壁粗糙有关量的变化共同构成管道粗糙系数n的不确定性。假设忽略过水面积尺寸的偏差对n值的影响，以钢筋混凝土为例，长期使用后通常取值范围为0.013～0.017，并且在这个范围内服从下三角形分布［9］，0.013 和 0.017 分别作为下限和上限，由此确定统计参数——平均值n、变异系数δn和标准差σn。

1.1.3 水力坡度J的不确定性

根据明渠均匀流的概念，雨水管内底坡度等于管道水力坡度，因而J的不确定性主要包括测量允许误差、施工验收允许误差和管道参数使用过程中发生变化造成的不确定性。考虑施工验收和测量允许误差，底坡J的变化范围:

GB 50014—2006《室外排水工程规范》(2011年修订版)中规定了雨水管道在不同管径下两检查井之间管内底高程的允许最大偏差与检查井在直线段的最大间距［10］。例如:雨水管道在不同管径下管内底高程的允许最大偏差在相邻两检查井之间满足:管径d＞1 000 mm时，允许最大误差为±15 mm;而当d≤1 000 mm，则为±10 mm。对于检查井在直线段最大间距为:管径200～400 mm，雨水管道最大间距40 m;管径500～700 mm，雨水管道最大间距60 m;管径800～1 000 mm，雨水管道最大间距80 m。

根据式(10)，可以得出水力坡度的变化范围，并假设在变化范围内服从三角分布，从而确定平均值变异系数 δJ以及标准差 σJ。

1.1.4 计算模型NR的不确定性

针对雨水管道设计的结果，Yen和Sevuk进行相关的统计研究，分析结果表明［2］:参数NR的平均取值=1.1，在0.8 ～1.4 范围之间遵从三角形分布。经计算，模型的变异系数δNR和标准差σNR分别为0.111 和0.122 1。

1.2 基于节点q的不确定性

众所周知，雨水管网设计流量按照强度极限理论推理公式进行计算，而它是假设降雨频率与城市雨水设计流量相同的。所以，设计流量的不确定性由降雨强度、径流系数以及汇水面积这些随机变量组成。此外，还应考虑计算模型的不确定性，则

式中:qS为节点汇水设计流量，L/s;ψ为径流系数，φ＜1;F为汇水面积，hm2;Qj为设计暴雨强度，L/(s·hm2);NS为推理公式模型化误差修正系数。

实例中，城区综合径流系数ψ的变异系数取0.07［11］，汇水面积 F 的变异系数取 0.05［12］。对于小积水面积排水，可取初步估计平均值=1.0，变异系数 δNS=0.15［13］。我国城市暴雨公式的一般形式如式(12):

式中:T 为重现期;t为降雨历时;A，C，b，c为参数，不同的城市拥有不同暴雨公式参数。变异系数δQj可取0.177［11］。

假设式(11)各随机变量相互独立，采用一次二阶矩法来确定qS的均值、变异系数 δQS和标准差σQS。

1.3 功能函数与极限状态方程

对于已建雨水管网节点在其各管道输水能力和节点汇水流量的各参数变量的情况下，管网任意节点可靠度的功能函数Z确定如式(13):

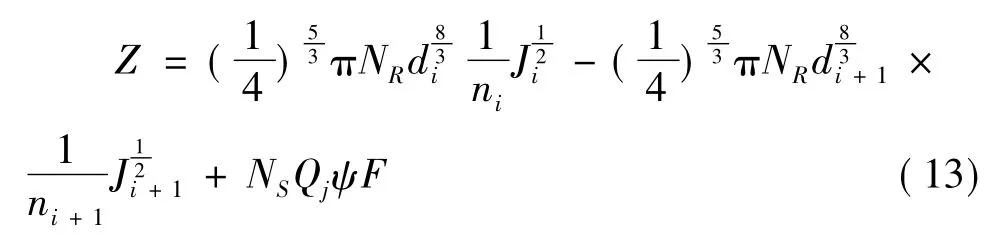
式中:变量意义同前。

由前面变量的不确定性可知，ψ，F，NS，q的概率分布不易确定，因此，这几个量的不确定性采用随机变量QS来代替，并假定概率在其合理范围内服从极值I型。为了简化模型，假定其余变量均服从正态分布，则功能函数变为:

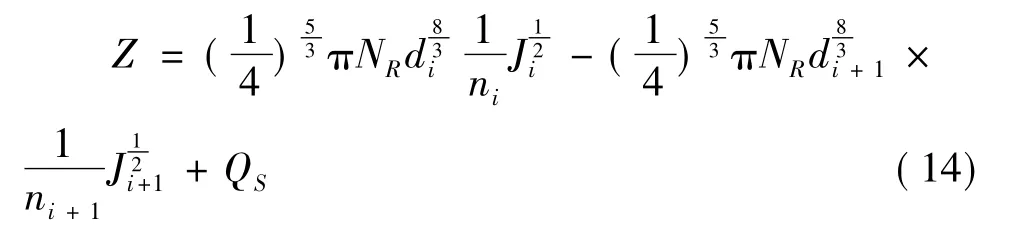
即

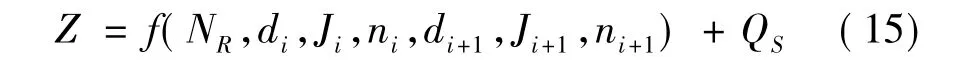
极限状态方程为:

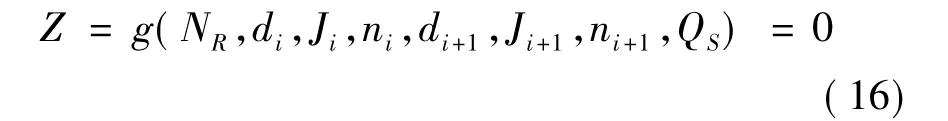
式(16)中含有8个变量。

1.4 节点可靠度的计算

目前结构可靠度比较常用的计算方法有JC法、Monte-Carlo法。采取JC法时，式(14)为非线性关系，变量较多，计算时需运用泰勒级数式线性展开，加之QS是非正态随机变量，需进行当量正态化方可计算。由于非线性功能函数线性化和非正态随机变量当量正态化的简化，所得计算结果的准确性不高。而Monte-Carlo法，当抽样次数N大于某一大数时，可靠指标收敛于一个恒定值，此时能够直接抽样统计计算结构可靠度，计算时没有进行简化，因此计算的结果准确性高，方法可靠。目前随着计算机的快速发展，采用Monte-Carlo法越来越体现出它的优势，因此，笔者采用Monte-Carlo法进行计算。

1.5 管网系统可靠度的计算

结构体系最基本类型有串联体系和并联体系两种。可靠度的分析是将其转化为多个失效模式的串联结构体系。因此，在工程结构中，体系可靠度问题就可以简化为串联结构体系问题进行计算。

就串联结构体系而言，可靠度计算方法常用的是区间估计法，包括宽界限法和窄界限法两种。窄界限法关键是要考虑失效模式间的关系，管网各节点以及节点与上下游管道之间或多或少存在某种拓扑关系，加之窄界限估算法要比宽界限估算法计算的范围集中，因此，采用窄界限法更合理。本文计算实例采用窄界限估算法，理论计算具体步骤参见文献［11］。

2 管网可靠度计算实例

某城区局部雨水市政排水系统管道运行历时5年，起初按照重现期1年考虑的市政排水管网，通过极限强度理论设计各市政管道流量。各节点汇入流量按当地暴雨公式，重现期1年，采用式(11)计算而得。具体相关水力计算参数如表1。

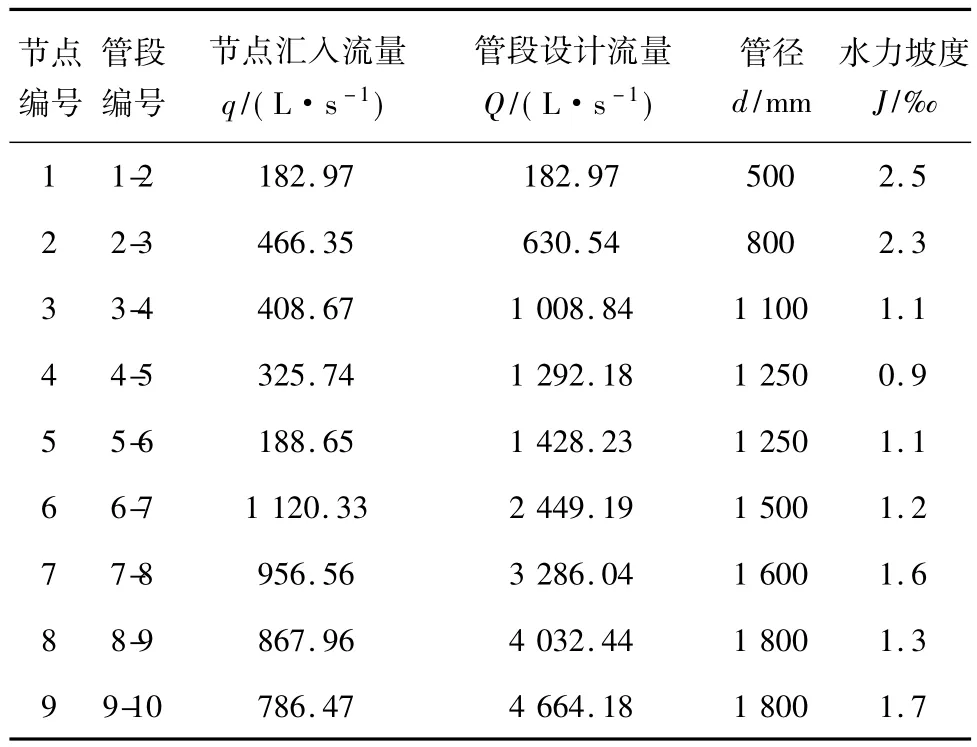
表1 雨水管网设计水力计算Table 1 Hydraulic calculation table of rainwater pipe network design

2.1 节点的可靠度计算

表2列出了节点2可靠度变量统计参数的计算结果，各随机变量统计参数按前面介绍的方法计算，其中节点2汇水流量的变异系数取0.25，服从极值I型分布。

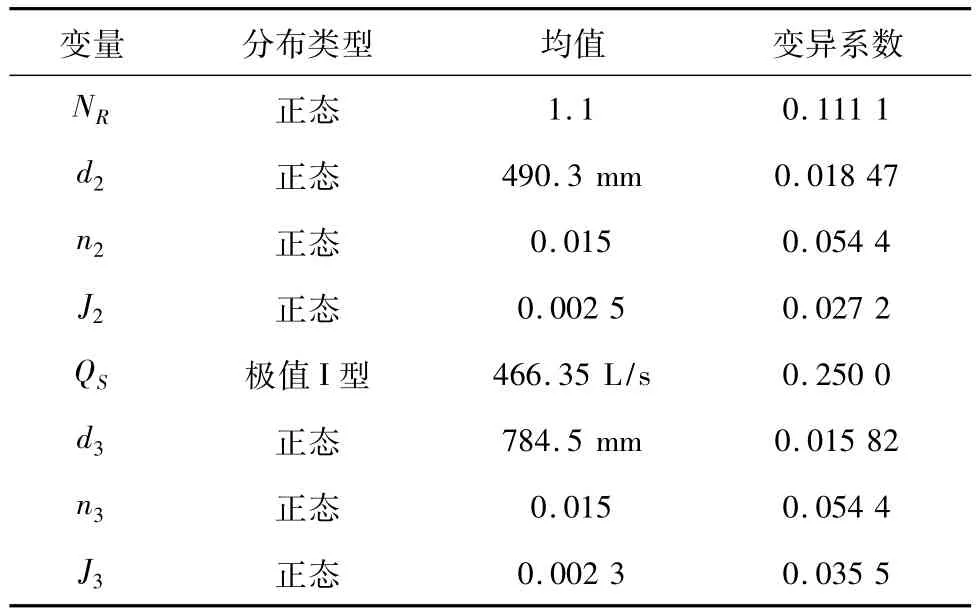
表2 节点2可靠度的变量统计参数Table 2 The variable statistical parameters for reliability of node 2

Monte-Carlo算法流程见图2，不同抽样次数N的可靠度MATLAB计算程序运行结果见表3。表中的值是随机一次模拟运行计算的，在抽样次数N＜5×106时，计算结果不收敛，随着抽样次数N的增加，计算量增大，耗用计时增长，收敛越快，可靠度逐渐趋于稳定。从程序运行计算过程可以看出，节点2 可靠度为 0.338 3。

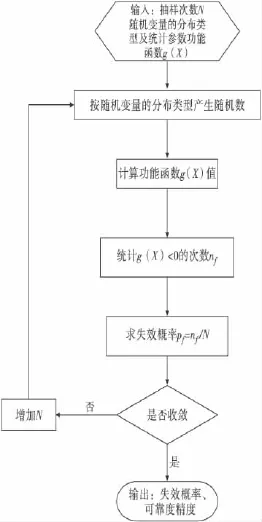
图2 Monte-Carlo算法流程Fig.2 Monte-Carlo algorithm flowchart

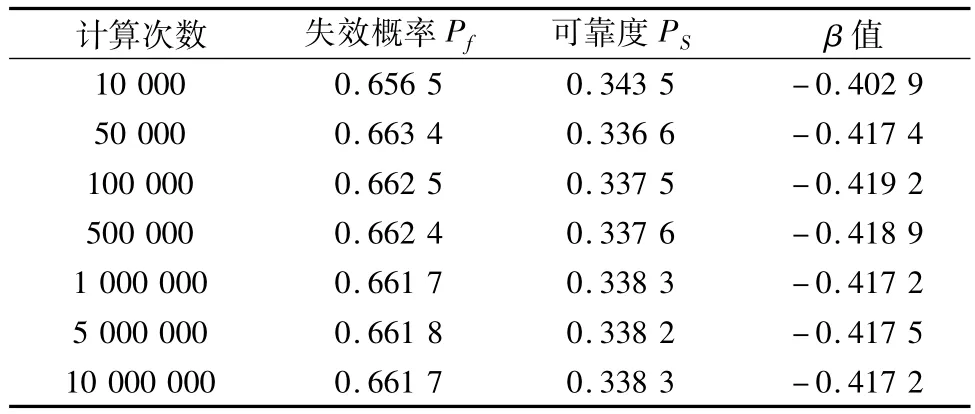
表3 用Monte-Carlo法计算节点2可靠度的结果Table 3 Results of 2-node reliability using Monte-Carlo method

2.2 管网可靠度计算(窄界限法)

从管网平面布置上可以看出，雨水管网体系的各管道间既有串联，也有并联关系，是并联和串联的组合关系。然而，雨水管网体系从管道失效模式间逻辑关系上来看是串联体系，而串联体系其本身是按照失效模式间的逻辑关系来定义的［14］。因此，采用串联体系可靠度的窄界限法对实例中管网系统的可靠度进行计算，其体系可简化为图3。

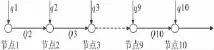
图3 管网体系计算模型Fig.3 Computing model of network system

首先，计算各节点失效模式的可靠度，采用JC法，各变量的统计参数在模式下都是相同的，即计算方法都与节点2类似。然后采用窄界限法的区间估计法来估计该管网体系可靠度。根据前面介绍的窄界限法得到该雨水管网的失效概率Pf的窄界限概率，综合运用MATLAB 编程计算得:0.605 0≤Pf≤0.899 3，则其相应的体系可靠度为:0.100 7≤PS≤0.395 0。

3 结论

基于节点的管网可靠度分析，可以得出以下结论:

1)从系统节点的不确定因素出发，通过节点可靠度的分析，继而研究讨论了雨水管网系统的可靠性问题，加强了节点与管段的联系，使对系统可靠度的把握更加准确。

2)成功运用了结构中的可靠度理论，首次提出通过强降雨时常发生事故的各检查井节点来讨论管网可靠度，通过计算结果来看是可行的。

3)在影响节点可靠度的管道输水量的分析中，增加了管道泥沙淤积和沉淀等不确定性对管道有效管径和粗糙度的影响，使得节点可靠度更具合理性。

4)实例分析系统可靠度的结果表明:既有雨水管网节点和系统可靠度都较低，这一客观事实的存在意味着当发生设计重现期和超过设计重现期的暴雨时，管网系统节点出现积水或者涌水以及整个管网系统不能及时排泄设计雨水流量的概率较大。这一结论与目前既有雨水管网的现状相符合。因此，制定切实可行的管网系统可靠度标准，提高体系可靠性是非常必要的，也是合理的。要提高管网系统可靠性，必须首先提高各节点的可靠度，才能保证整个系统的稳定和安全。

［1］ 赵子成，禹华谦.城市突降暴雨排水管网节点处积水量计算研究［J］.城市道桥与防洪，2012，28(2):57-58.

Zhao Zicheng，Yu Huaqian.Study on calculation of flowage amount at urban drainage network node under an unexpected intense fall［J］.Urban Roads Bridges ＆ Flood Control，2012，28(2):57-58.

［2］ 周玉文，赵洪宾.排水管网理论与计算［M］.北京:中国建筑工业出版社，2000.

［3］ 张子贤.基于可靠性的雨水管道水力设计方法［J］.给水排水，2001，21(17):10-12.

Zhang Zixian.Hydraulic calculation based on reliability of storm water pipeline［J］.Water and Wasterwater，2001，21(17):10-12.

［4］ 郭瑞，禹华谦.雨水管道的概率极限状态水力计算［J］.中国给水排水，2006，22(24):51-54.

Guo Rui，Yu Huaqian.Hydraulic calculation of probability limit state of rainwater pipeline ［J］.China Water and Wasterwater，2006，22(24):51-54.

［5］ 张建仁，刘畅.结构可靠度理论及其在桥梁工程中的应用［M］.北京:人民交通出版社，2003.

［6］ 禹华谦.工程流体力学［M］.2版.北京:高等教育出版社，2011.

［7］ 郭瑞.基于可靠性的城市雨水管网水力计算研究［D］.成都:西南交通大学，2005.

［8］ GB/T 11836—1999混凝土和钢筋混凝土排水管［S］.北京:国家技术监督局，2000.

［9］ 董颖.排水管网系统改扩建优化设计研究［D］.西安:西安理工大学，2006.

［10］工程建设标准规范分类汇编.室外排水工程规范［M］.北京:中国建筑工业出版社，1996.

［11］洪华生，邓汉忠.工程规划与设计中的概率概念［M］.大连:冶金工业出版社，1991.

［12］严煦世，刘遂庆.给水排水管网系统［M］.北京:中国建筑工业出版社，2008.

［13］周玉文，李振华，曹丽虹，等.排水管网可靠性计算基础［J］.沈阳建筑工程学院学报，1998，14(2):105-108.

Zhou Yuwen，Li Zhenhua，Cao Lihong，et al.Reliability caculation base of drainage pipe line［J］.Journal of Shenyang Architectural and Civil Engineering Institute，1998，14(2):105-108.

［14］ Low B K，Tang W H.Efficient reliability evaluation using spread sheet［J］.Journal of Engineering Mechanices，1997，123(7):33-37.