锚失效影响岩质边坡稳定的数值模拟

李 强，唐树名

(1.重庆市设计院，重庆400015;2.重庆交通科研设计院，重庆400067)

有限元法是数值计算中发展较早、应用最广的一种方法，到目前为止，该方法在岩土工程中获得成功的应用并积累了丰富的工程经验和较成熟的处理技术。随着计算机软硬件技术的快速发展，目前已经出现了许多大型有限元软件，ANSYS就是其中一种。该软件的优点在于，具有很高的可靠性、十分方便的前后处理以及高效齐全的算法组合。应用该软件，可以节约时间、提高工作效率并提高计算成果的可靠度。它具有强大的静力分析、动力学分析、非线性分析、优化设计和可靠性分析等结构分析能力，笔者采用ANSYS软件对“设置格子梁的锚失效影响岩质边坡稳定性”进行了有限元数值模拟分析。研究不同位置的锚失效后其它锚的荷载重分布规律以及锚失效后边坡的承载能力变化。

1 锚固边坡有限元模型的建立

1.1 模型单元的选取及材料的本构关系

模型分析采用ANSYS软件进行分析［1］，其中坡体与格子梁分别采用两种20节点金字塔等参单元20Node95来模拟，金字塔单元是三维体单元，不仅可以单独使用，还可以作为过渡元使用。作为过渡元使用时有10节点四面体单元、15节点五面体单元和20节点六面体单元。单独使用时是三维20节点六面体单元，这个单元是二次线性单元，很适用于模拟复杂边界的实体。因此，对于空间实体结构分析，特别是具有过渡段的实体结构分析非常适用，而且精度较高。锚索、锚杆模型材料中锚采用拉索单元Link10模拟，其为双线性单元，允许只拉和只压，由于实际边坡中锚索主要承受拉应力故本次分析只考虑锚索拉应力作用。由于锚索实体材料是钢绞线，模拟材料采用铜丝均属于弹性材料，通常在岩体中考虑采用的是它发挥的弹性部分，故在计算中采用线弹性模型［2］。

坡体材料的本构模型采用较好反映岩体扩容性质的Drucker-Prager模型。

Drucker-Prager是考虑静水压力影响的广义Mi-ses屈服与破坏准则，简称D-P屈服或破坏准则。屈服函数为:

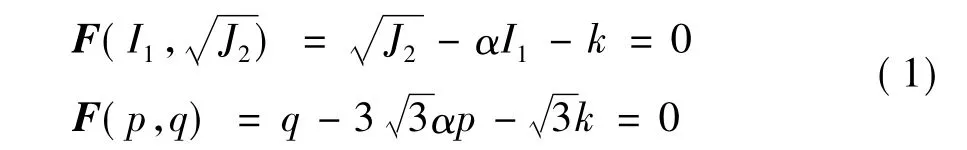
式中:α和k为D-P准则材料常数;p为平均应力;q为应力强度;I1为应力第1不变量;J2为应力偏张量第2不变量。坡体的模型参数参考向家坡实体工程参数，结合材料实验得出的数据综合考虑。

锚索模型材料的本构模型采用符合金属材料特性的Mises理想弹塑性模型。Mises准则是同时考虑3个主应力影响的能量屈服准则，其屈服函数可以表示为:

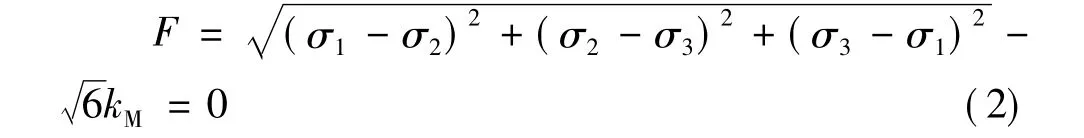
式中:kM为Mises材料屈服常数，由试验确定，当进行单向拉压试验时，kM=σs/3，当进行纯剪切试验时，kM=τs;σ1，σ2，σ3为3 个主应力。

1.2 模型材料参数的选取

边坡稳定计算中关键因素是结构面的摩擦系数tanφ和黏结力c，因此在数值分析中该值的选取尤为重要，为了与实验分析相匹配，该数据的选取参考了两种方法。

1.2.1 加载静力分析法(图1)

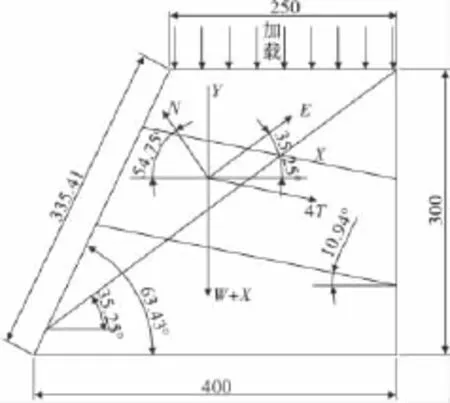
图1 坡顶加载解析法计算Fig.1 Calculation method of slope under loading

通过实验数据分析，无锚时坡顶加载50 kg，达到边坡稳定临界状态:

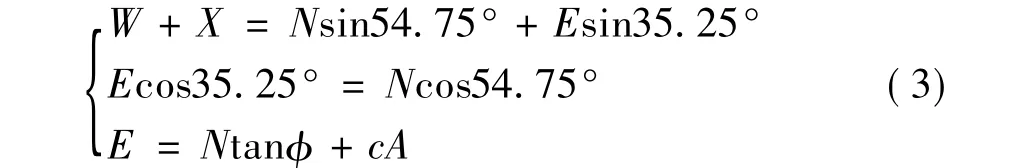
式中:W为滑面上坡体自重，W=γV=194.4 N;X为坡顶加载，X=500 N;N为垂直于坡面的压力，N;E为坡面抗滑力，N;tanφ为结构面摩擦系数;c为结构面黏结力，kPa;A为结构面面面积，A=0.3×0.387=0.116 1m2。

由式(3)可以求得:

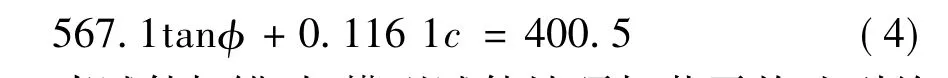
当试件加锚时，模型试件坡顶加载平均达到约11 t时结构面破坏，边坡达到极限状态，此时可以得到以下平衡方程:

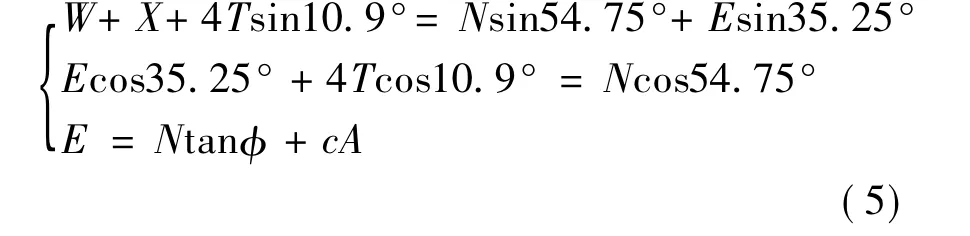
式中:T为锚索拉力，取实验平均数据T=1 000 N，得到:

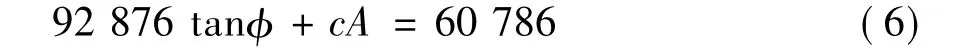
由式(4)和式(6)求得:tanφ =0.654，c=0.255 kPa。

1.2.2 模型有限元分析计算参数的确定

通过模型材料实验进行选取模型试件内结构面采用1 mm厚的白铁皮进行模拟，通过DSJ-Ⅰ型电动四联应变直剪仪测得其抗剪参数c=4.89 kPa，tanφ =0.644(φ =32.78°)。

比较两种方法，得出的结果基本一致。综合两方面因素的考虑，结合相似比关系，从偏保守考虑，模型有限元分析中采用抗剪参数 c=4.89 kPa，tanφ =0.644(φ =32.78°)。其它各种材料的本构模型参数通过实验确定，格子梁的参数未采用实验中硬木条数据，采用的是按照相似比计算的C20混凝土参数，这与实际的工程相符合，但与实验中采用硬木条的参数有一定区别，各参数详见表1。

表1 模型有限元分析计算参数Table 1 Calculative parameters of finite element analysis

1.3 有限元模型建立

1.3.1 网格划分与结构面的模拟

模型单元共分为4类，分别为solid95，Link10，Targe170，Conta174。Solid95为三维实体单元用来分别模拟模型岩体结构和格子梁结构，Link10用来模拟锚索，锚索仅能承受拉应力，采用空间2节点杆单元来模拟，每个节点的自由度为空间3个方向的位移。Targe170，Conta174用来模拟结构面，上下岩体间的结构面采用接触面近似模拟，给出接触面的摩擦系数 tanφ =0.644，c=4.89 kPa(图2)。网格单元划分均以线性控制，坡体单元边尺寸控制为50 mm，格子梁单元边尺寸控制为15 mm(图3)。岩体划分中注意锚索处需作为控制线进行单元节点划分。在格子梁和边坡面相交处以共节点glue黏结。有限元模型的尺寸与实验试件的尺寸相一致，设锚与结构面位置均与实验中的位置一一对应。

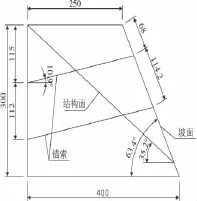
图2 模型结构示意Fig.2 Finite element analysis model

图3 模型单元划分Fig.3 Mesh of the model’s cell

1.3.2 约束处理施加方案

试件的约束分别给底面施加全部约束，后端面给予垂直端面方向约束，两个侧面给予垂直该侧面方向约束，前端面即坡面处自由状态，坡体可以向坡面处自由滑动。

1.3.3 施加荷载方案

首先给坡体施加自重，然后坡顶采用逐级加载的方法，每次施加均布荷载增量值为10 kN(133 kPa)，直至计算模型塑性区扩大到一定程度及范围后(坡体位移大于10 mm)或坡体不能继续承载为止，最大加载为110 kN，此时试件临界破坏。

1.3.4 锚索预应力的施加

预应力锚索的预应力的施加通过给锚索施加初始应变来实现，故计算时根据锚索预应力的大小，给锚索施加初始应变来模拟，式(7):

式中:Δε0为初始施加预应力锚索应变值，mm;σp为锚索预应力，kN;Eg为锚索弹性模量，kN/mm。

在有限元分析中，锚索的预应力效果采用施加应变的方式来处理。加载时，根据预拉荷载F=400 N，指定锚索杆单元产生一个初始收缩应变ε0=1.6×10－3。由于锚索杆单元与岩坡实体单元公共节点采用相同的节点编号，从而使岩坡实体单元相应节点产生相应的压缩位移量及相应的压应力和压应变，使得锚索各个杆单元产生的预应力全长有效地传到岩坡中，达到对岩坡施加预压应力的效果，而传统的施加一对集中力的方法则不能达到这种效果。最终的计算结果亦表明该方法能对预应力锚索预应力加载效果进行较好地模拟。缺点是忽略了锚索可能出现自身的缺陷以及自身出现的不均匀受拉和复杂受力状态。

锚失效与锚索预应力损失是不同的，锚失效是全部或者大部分的锚索预应力已经损失，锚索已经基本起不到加固边坡的作用，而锚索预应力损失则表明锚索已经损失了部分预应力，但仍能起到一定加固边坡的作用。数值模拟中忽略了锚索预应力损失的变换过程，简化为锚失效，即锚完全起不到加固边坡的作用。

1.4 有限元中边坡失稳的判据

在边坡有限元数值计算中失稳判据的选择很重要，数值模拟分析有限元加载过程中边坡失稳主要有以下判据［3-4］。

1.4.1 有限元解的不收敛

该方法认为当边坡处于极限平衡状态时，非线性有限元方程组的迭代过程将不收敛。由于收敛的标准通常是由用户指定的失衡力的大小来控制的，且不收敛可由很多其他因素而引起，并不一定意味着结构已经崩溃，因此这一标准相对缺乏客观性。

1.4.2 边坡内某一特征点的位移发生突变且无限发展

以某个特征点为标准，认为当边坡达到极限状态时，某些点的位移会趋于流动状态，这在理论上是正确的，但在选取特征点时应非常慎重;否则在某些复杂情况下选取不同的特征点，可能会得出不同的安全系数。此外，取位移强度折减系数曲线上的哪一点作为极限状态尚未取得共识。

1.4.3 广义剪应变标准或广义塑性应变标准

广义剪应变通常既包括弹性应变，也包括不可恢复的塑性应变，尽管广义剪应变的大小能够在一定程度上反映岩土的相对变形状态，但是并不能准确地表述实际塑性区的发生与发展过程，因此以此作为失稳指标是不确切的。塑性应变的发生与发展表明了岩土体屈服或破坏的发生与发展程度，表示屈服或破坏岩土体内所发生的变形中的不可恢复的残余变形分量。因此塑性应变的大小能够从本质上描述岩土体的屈服或破坏发展过程，采用塑性开展区的相互贯通评判岩土体的整体失稳破坏是比较合理的。对于平面应变问题，广义剪应变εd与广义塑性应变分别可表示为:

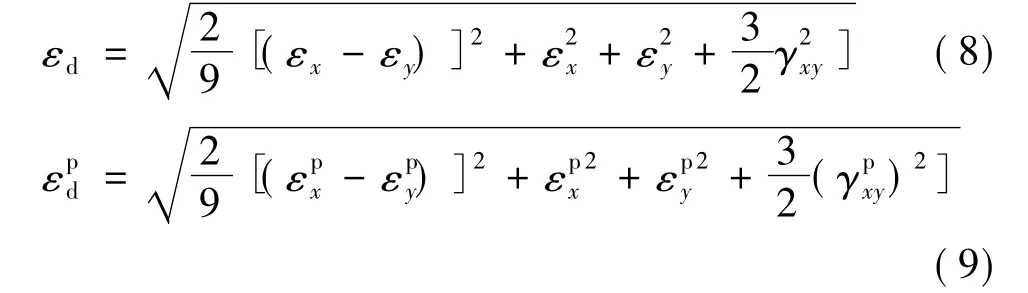
文献［5-6］认为，当边坡达到极限平衡态时，广义剪应变或广义塑性应变的等值线图中，必有一条等值线，通常是数值较小的那条等值线，由坡底贯通到坡项。这一标准相对比较合理。但是，由于坡内应变值的大小与岩土材料的软硬程度是密切相关的，当坡内含有软硬相差很大的材料时，广义剪应变或广义塑性应变的等值线图将会非常怪异，此时需改用塑性功等值线图来弥补这一不足。

1.4.4 能量准则

由郑宏，等［7］及邵国建，等［8］提出的基于能量准则的岩体稳定性分析方法是一个在概念上有别于经典极限平衡法的分析方法。该方法是通过干扰能量等值线图来确定潜在滑面的。为了得到单元的干扰能量，需考虑系统的几何非线性，计算中会涉及到几何刚度矩阵的求逆和特征值问题的求解，其运算量和存贮量甚至高于应力分析本身。虽然一般情况下，所求得的安全系数及其潜在滑面都不同于经典的极限平衡法，但这仍然是一种很有前景的研究方法。

综合分析了各种有限元中边坡失稳判据，本次计算采用的失稳判据主要是边坡内某一特征点的位移发生突变且无限发展，有限元解的不收敛以及锚索受力不得超过1 500 N。

1.5 锚失效机理分析

目前工程界认为几种锚固破坏模式［9］主要有:钢铰线与浆体材料黏结面破坏，钢绞线拉出;锚索孔注浆体与周围岩体黏结强度不足，围岩破坏;钢铰线本身被拉断;被加固岩土体的破坏;外锚头的破坏，致使锚索预应力损失，直至失效;被钢铰线分割的浆体材料块体之间的分离破坏。无论何种锚失效的形式，都意味着锚失去了加固边坡的作用，笔者关于锚失效的模拟进行了简化，仅考虑锚失效后，无法起到加固边坡的作用，此时锚索作用力为0。

2 有限元计算结果分析

2.1 坡面设梁逐级加载时不同锚失效后其它锚受力及坡体位移变化(表2)

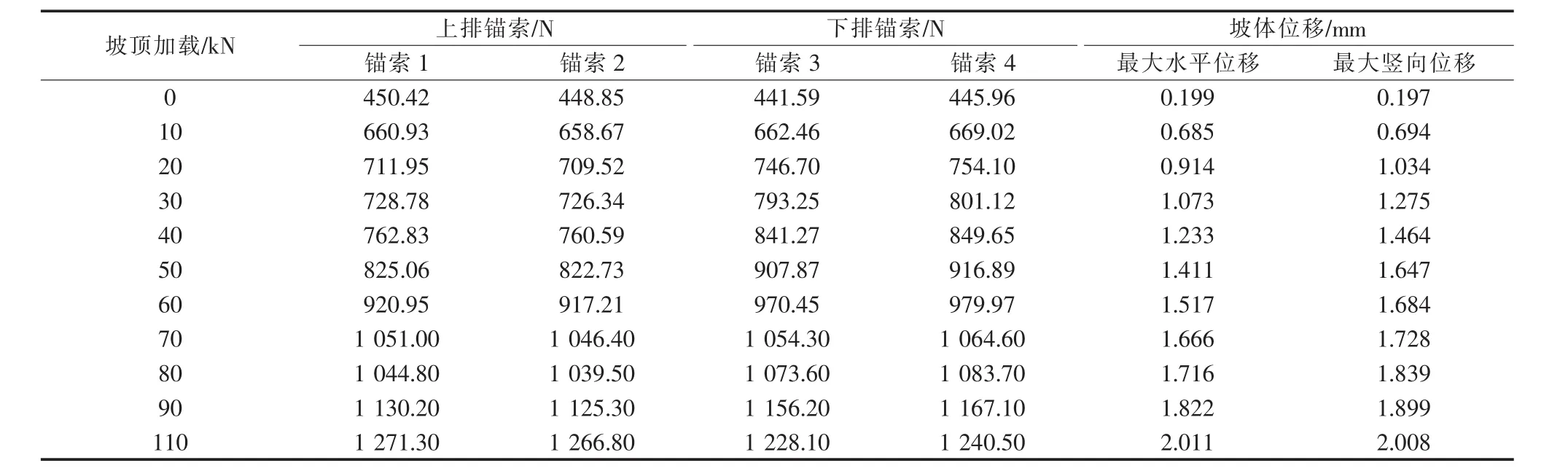
表2 设置纵横梁试件加载计算结果Table 2 Loading results in specimen set with anchors on grids

由表2可以发现:

1)随着逐级加载，坡体和锚索受力不断增大，边坡位移不断增大。竖向位移大于水平位移，这主要是因为试件在受压后既有一定滑动，同时又被压缩。位移数值相对实验数值偏小，主要是计算中试件采用的是理想弹塑性材料，而实验中的试件缺陷较多。

2)在坡体自重作用下，锚索初始施加预应力，开始既能提供较大的初始预压力，锚固作用良好。由于设有纵横梁，锚索可以通过纵横梁，形成格子结构，扩大了施加坡体的压应力面。

3)对比表2中上排锚索1、锚索2与下排锚索3、锚索4受力可以发现，下排锚索受荷一直大于上排锚索受力，但锚索受力相对比其它梁结构更均匀，而且较其它情况如纯锚试件、有纵梁试件和有横梁试件均较小。说明纵横梁能起到分担部分压应力，平衡锚索受力的作用。这与实验基本符合。

4)在锚索作用的纵横梁处有应力集中现象，在锚力作用处需加强结构措施以避免应力集中产生的破坏。竖向最大位移与水平最大位移发生处均与其它试件相同。与实验基本吻合。

锚索的失效模拟通过有限元操作中生死单元的设置得以实现，杀死需要失效的锚索杆单元，然后继续进行计算，可得出剩余锚索的荷载重分布后的值。

2.2 坡面设梁分别加载8 t和4 t时不同锚失效后其它锚受力及坡体位移变化(表3)

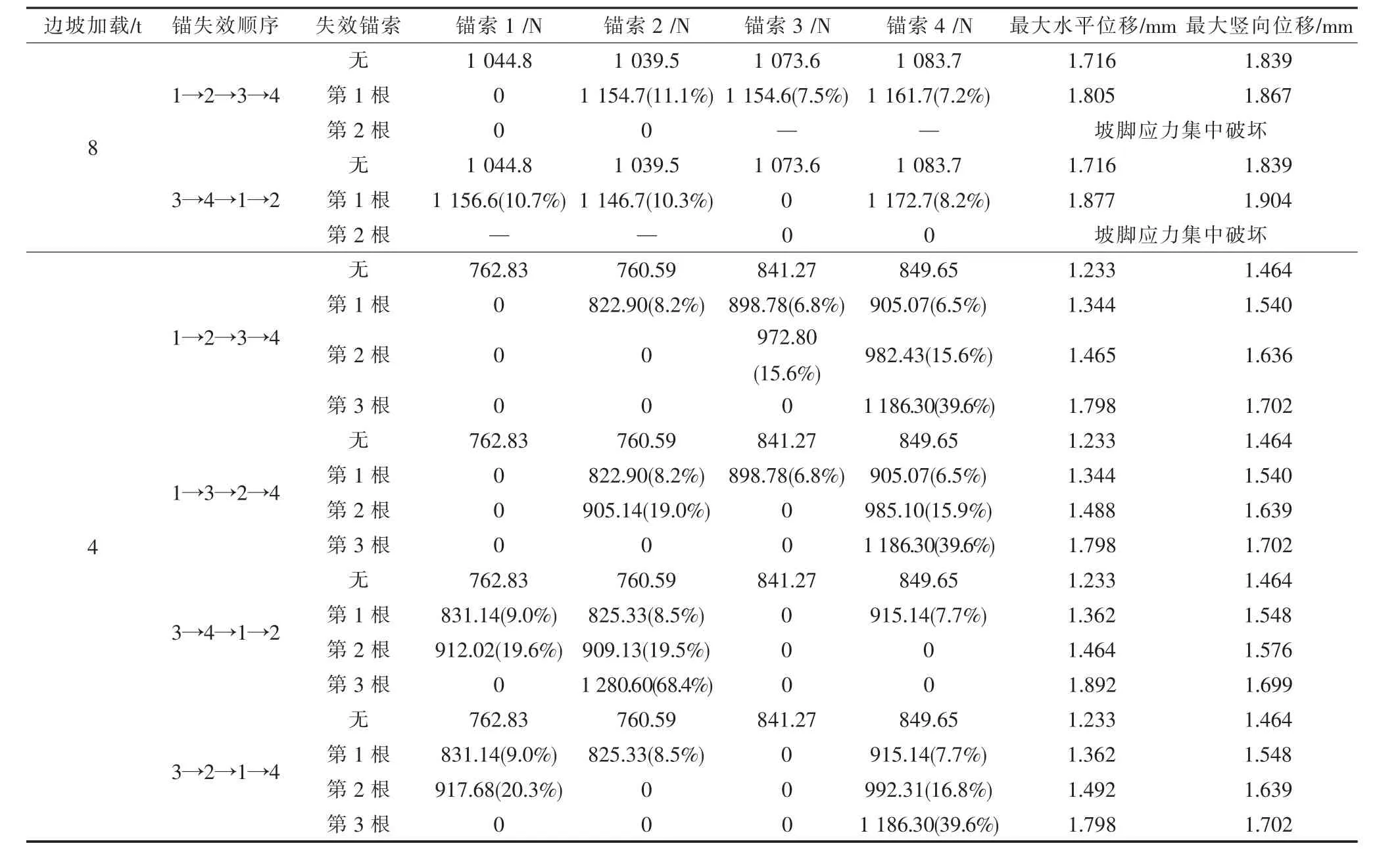
表3 设纵横梁边坡加载时不同锚索失效后其它锚受力及坡体变化Table 3 Changes of tensile force of other cables and displacement of slope after deactivating different cables on grids by loadings

从表3可以看出:

1)任一根锚索的失效均产生不同程度的应力重分布作用，其它锚索均能分担锚失效后的部分不平衡力。同时随着锚索的逐根失效边坡位移均不断增大，直到坡体破坏或失稳。

2)单锚失效。在坡顶较大加载，即加载8t时，上排锚索1失效，锚索2～锚索4承受的拉力分别增加了 115.2，81，78 N，同比增加了 11.08%，7.54%，7.20%。下排锚索3失效后，上排锚索1、锚索2和下排锚索 4受力分别增加了 111.8，107.2和89.0 N，同比增加了 10.70%，10.31%，8.21%。可以发现上排锚索受力同比增加较多。

在较小加载时，即加载4 t时，上排锚索1失效，锚索2～锚索4承受的拉力分别增加了68.3，57.51，55.42 N，同 比增加 了 8.19%，6.84%，6.52%。下排锚索3失效后，上排锚索1、锚索2和下排锚索4 受力分别增加了68.31，64.74 和 65.49 N，同比增加了 8.96%，8.51%，7.71%。

总的看来，在单锚失效时，其它锚索受力均有一定提高，受力增加了6.5%～11%。下排锚失效后上排锚分担荷载有较大提高，达到了 8.19% ～11.08%。由于有纵横梁作用，锚索受力相对比较均衡。锚索失效后上排锚索分担的不平衡力增加率大于下排锚索。

3)两根锚索失效时，在施加高荷载8 t时边坡坡脚已经破坏，其它两根锚索失效，边坡处于不稳定状态。

在施加低荷载4 t时上排锚索1、锚索2全部失效时，下排锚索3、锚索4受力比未失效时分别增加了 131.56，132.78 N，同 比 增 加 了 15.64%，15.63%。下排锚索3、锚索4全部失效时，上排锚索1、锚索 2受力比未失效时分别增加了 149.19，148.54 N，同比增加了 19.56%，19.53%。当一列的两根锚索1和锚索3失效后，相邻一列的2根锚索2和锚索4受力分别增加了144.55，135.45 N，同比增加了19.05%，15.94%。交错对位处锚索2和锚索3失效后，锚索1和锚索4受力比未失效时增加了154.85，142.66 N，同比增加了 20.30%，16.79%。

总体来说在2根锚失效时，在低加载时锚索受力均增加了15.6%～20.3%，同样在其它锚失效后上排锚索受力增加率较大。在高加载情况下坡脚已经破坏，坡体失稳。在较低应力情况下剩余锚索受力增加仍能维持边坡的稳定。

4)在出现3根锚失效的情况下，在较高加载8 t情况下，坡体均已失稳。在较低加载4 t时，当仅剩下排锚索4时，受力增加了336.65 N，同比增加了39.62%。在仅剩上排锚索2时，锚索受力增加了520 N，同比增加了68.37%。上排锚索受力增加率大于下排。

建立的有限元模型和边坡受力位移见图4～图6。

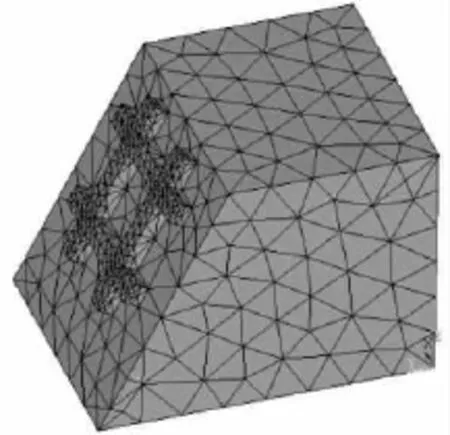
图4 设纵横梁试件网格划分Fig.4 Mesh of the model’s cell when grids are on slope

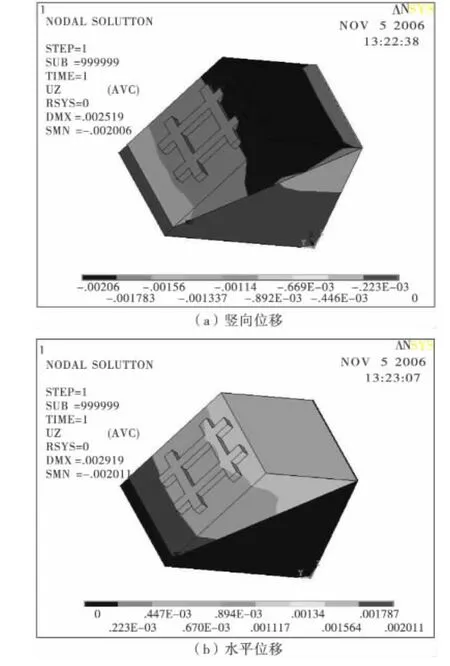
图5 设纵横梁试件加载后的位移Fig.5 Displacement of specimen with anchors on grids

图6 设纵横梁试件加载后的主应力Fig.6 Main stress of specimen set with anchors on grids

3 结论

分析了岩质边坡坡面设置格子梁情况下各锚受力特征和不同位置锚失效后其它锚的荷载传递规律和边坡破坏情况。得出如下结论:

1)锚索能够给予坡体主动支护力，大大提高坡体的承荷能力，能够约束边坡的位移，提高边坡的稳定性，是一种行之有效的加固边坡的方式。即使当边坡出现破坏时，边坡的破坏由脆性破坏转变为塑性破坏，有利于我们及时发现和消除隐患。需要注意在边坡直线滑动结构面处有较大的剪应力，在设锚索位置处有明显的应力集中现象。边坡失稳主要是边坡结构面的剪切破坏。

2)无论在什么位置的单锚失效，均对周边的锚索产生应力重分布，其它周边锚索均能分担单锚失效后的部分不平衡力。同时随着锚索的失效，边坡位移均不断增大。单锚失效时，周边其它锚索受力均有一定提高，受力一般增加了5% ～8%。在较低加载情况下应力重分布作用提高幅度比高加载时大。当两根锚失效时，在低加载情况时其它锚索受力均增加了12% ～20.3%。对位锚索失效后，其它锚索受力增加幅度相对较大。

［1］ 李权.ANSYS在土木工程中的应用［M］.北京:人民邮电出版社，2005.

［2］ 宋二祥.土工结构安全系数的有限元计算［J］.岩土工程学报，1997，19(1):1-7.

Song Erxiang.Soil structure safety coefficient finite element method［J］.Chinese Journal of Geotechnical Engineering，1997，19(1):1-7.

［3］ 连镇营，韩国城，孔宪京.强度折减有限元研究开挖边坡的稳定性［J］.岩土工程学报，2001，23(4):406-411.

Lian Zhenying，Han Guocheng，Kong Xianjing.Strength reduction finite element stability analysis of excavation ［J］.Chinese Journal of Geotechnical Engineering，2001，23(4):406-411.

［4］ 唐树名.碎裂结构岩体路堑边坡锚固机理分析及其应用研究［D］.重庆:重庆大学，2003.

［5］ 张永兴，许明.岩土锚固系统质量智能诊断理论与应用［M］.北京:中国建筑工业出版社，2002.

［6］ 栾茂出，武亚军，年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用［J］.防灾减灾工程学报，2003(3):l-8.

Luan Maochu，Wu Yajun，Nian Tingkai.Strength reduction finite element method for stability of slope in the plastic zone criterion and its application［J］.Journal of Disaster Prevention and Mitigation Engineering，2003(3):l-8.

［7］ 郑宏，李春光，葛修润，等.求解安全系数的有限元法［J］.岩土工程学报，2002，24(5):626-628.

Zheng Hong，Li Chunguang，Ge Xiurun，et al.Finite element method for solving［J］.Chinese Journal of Geotechnical Engineering，2002，24(5):626-628.

［8］ 邵国建，卓家寿，章青.岩体稳定性分析于评价准则研究［J］.岩石力学与工程学报，2003，24(5):69l-696.

Shao Guojian，Zhuo Jiashou，Zhang Qing.Rock mass stability analysis in the appraisal of guidelines for research［J］.Chinese Journal of Rock Mechanics and Engineering，2003，24(5):69l-696.

［9］ JTG D 30—2004公路路基设计规范［S］.北京:人民交通出版社，2004.