路面平整度评价指标IRI的影响因素

王建锋，宋宏勋，马荣贵

(1.长安大学陕西省道路交通智能检测与装备工程技术研究中心，陕西西安710064;2.长安大学信息工程学院，陕西 西安710064)

随着国民经济的发展，我国高速公路建设有了突飞猛进的进展。由于车辆行驶速度的提高，道路使用者对道路的使用功能，尤其对道路路面的平整度提出了愈来愈高的要求［1-2］。各种路面平整度测量方法不断出现，如目前广泛采用的反应类路面平整度测定方法。各种方法都有自己的评价体系和评价指标，为了使各种不同测量指标能够相互比较，因此建立了国际通用的路面平整度评价体系，即IRI评价体系。该标准体系中给定了固定参数的车轮模型，通过不同方法测量路面的高程值，然后把高程值导入该标准模型计算IRI。由于该模型的响应频率范围等限制，在实际中发现即使相同的路面高程，通过标准模型计算获得的IRI值也是有差异的，尤其是位移传感器的精度、数据采样间隔、检测方向、评价距离、以及检测车速等都对IRI的值有影响。

实际平整度检测中，IRI的检测结果受多种因素的影响，因此对IRI标准模型的影响因素进行研究是实际路面平整度检测中必须要考虑的问题，进行此研究有重要的实际意义和应用价值。

笔者采用数值模拟的方法，定量分析了检测系统中的位移传感器精度、信号的采样间隔、IRI评价距离、检测时的检测方向以及检测车速等因素对IRI的影响。

1 IRI

目前国际上通常采用IRI来表征道路路面平整度。IRI是应用力学的方法，模拟给定参数的车辆以一定速度通过道路路面时，车辆相对竖直位移的积累值与行驶距离的比值，单位用m/km表示。

1.1 1/4 车轮模型

各国为了使平整度指标具有国际通用性进行了大量研究，其中具有里程碑意义的是世界银行的46号报告。该报告确定把IRI作为国际通用的路面平整度评价指标，并给出了标准1/4车轮模型(如图1)［3-4］。按照此模型来计算检测路面的IRI值。

图1 1/4车轮模型Fig.1 1/4 wheel model for IRI calculation

对图1中的标准1/4车轮模型进行运动学分析，其运动方程为:

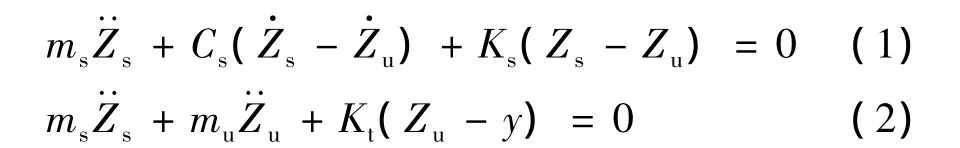
将式(1)、式(2)两边同时除以ms，则运动方程可以简化为式(3)和式(4):

式中:C=Cs/ms=6.00(1/s);u=mu/ms=0.150;K1=Kt/ms=653(1/s2);K2=Ks/ms=63.3(1/s2)。

可按式(5)计算L距离段内的IRI值:

1.2 IRI求解

由以上分析可知，IRI是通过求解式(3)与式(4)来实现的。由于路面纵断面的高程是离散的，因此通常利用数值法来求解。具体采用传递矩阵法，其求解过程如下。

将式(3)和式(4)的解转化为一个递归方程［5-6］，如式(6)～式(8):

上式中:z(i)是当前位置的状态量;z(i-1)是前一位置的状态量;Y(i)是当前位置前点与后点之间的纵向坡度;dx为数据采样间隔。

上式中:n为采样次数;I为单位矩阵。

通过求解以上的递归方程，计算出˙zs，˙zu，然后按照式(13)计算IRI。

2 IRI影响因素分析

实际检测过程中，IRI的精度主要受位移传感器精度、数据采样间隔、IRI评价距离、测量方向以及测量速度等多方面的影响。笔者即对这些影响因素进行定量研究。

2.1 位移传感器精度

IRI计算是以获取测量路段的路面纵断面相对高程为前提的。路面纵断面相对高程的测量通常利用位移传感器来实现，因此，测量用位移传感器的精度必然会影响IRI的计算精度。设测量路面的相对高程为f(xi);位移传感器的精度为Δ，此精度传感器的测量误差为δi=±Δ。因此，位移传感器测量得到的路面高程yi=f(xi)+δi=f(xi)±Δ。

目前，在路面平整度检测中广泛使用的位移传感器的精度主要有 1.0，0.5，0.4，0.3，0.2，0.1 mm等几种［7］。假设测量路面的纵断面高程f(xi)=0，不同位移传感器精度对IRI的影响结果如图2。

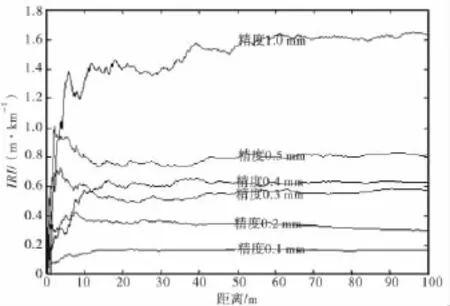
图2 传感器精度引起的IRI测量误差Fig.2 IRI error curve caused by different sensor precision

从图2可以看出:位移传感器精度越高，IRI测量误差就越小。因此，在实际检测过程中只有提高位移传感器精度才能减小IRI的测量误差。

2.2 数据采样间隔

每段路面都具有微观凹凸不平的纹理，实际检测过程，利用激光位移传感器测量的路面高程中必然叠加有路面的纹理值。因此，为了提高IRI测量精度，通常采用大密度采样，然后计算平均值以此来减小纹理的影响。可见数据采样间隔对IRI测量结果必然产生影响。

笔者利用常用几种精度的位移传感器，以不同的采样间隔进行数据采集，利用所得数据计算IRI的误差。数据采样间隔为10 mm时，不同精度位移传感器测量IRI时的误差曲线见图3，其余采样间隔下，常见的几种精度位移传感器测量IRI的误差值见表1。

图3 10mm采样间隔时传感器精度引起的IRI测量误差Fig.3 IRI error curve caused by sensor precision in 10mm sample distance

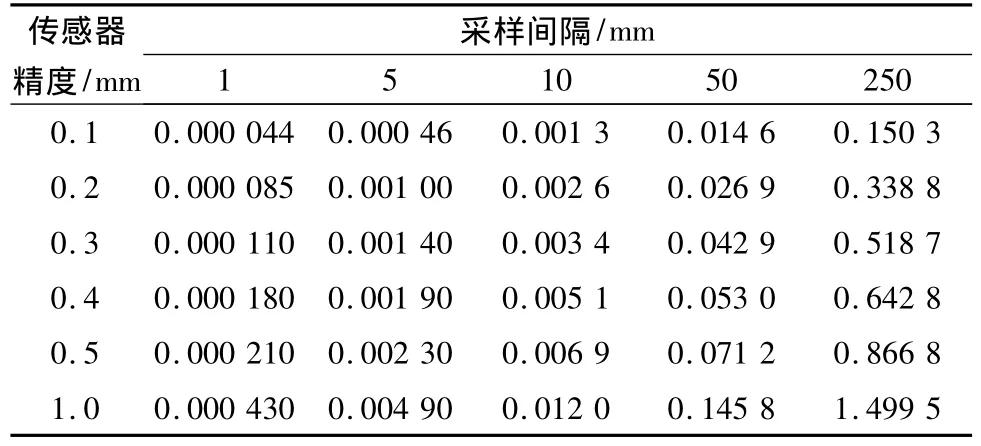
表1 采样间隔与传感器精度引起的IRI测量误差Table 1 IRI error caused by sample distance and sensor precision/(m·km－1)

从表1中能够看出:位移传感器精度越高、数据采样间隔越小，IRI测量误差就越小。位移传感器精度相同时，数据采样间隔越小，IRI测量误差越小。

2.3 评价距离

因为IRI计算是以路面纵断面为前提的，所以，选择的计算距离对IRI的精度也有影响。

本文设置如图4所示的一段路，该路在30～40 m之间有一个2 mm弧形突起，其余距离处为光滑路面，即高程为0。为了分析方便，假设位移传感器没有测量误差，数据的采样间隔为1 mm，结果如图4。

图4 评价距离对IRI测量的影响Fig.4 Influence of measure distance on IRI error

从图4可以看出:计算距离分别为100，200，300 m时，IRI=0.07，0.03，0.02 m/km。可见，不同计算距离引起的IRI误差有所差异，评价距离越长IRI误差越小，但是评价距离太长，所得IRI在路面养护中的实用性越差，因此，平整度检测规范中规定IRI的评价距离为100 m。

2.4 检测方向

采用的路面同图4，位移传感器没有测量误差，数据采样间隔为0.1 mm，误差结果如图5。

图5 检测方向对IRI测量的影响Fig.5 Influence of measure direction on IRI error

从图5中可以看出:检测方向正向时，IRI=0.077 m/km;逆向时 IRI=0.076 m/km。可见计算方向对IRI影响较小。

2.5 检测车速

世界银行给定的IRI标准模型中，假定的测试速度为80 km/h，实际检测过程并不能保证检测车速为此恒定值［8］。采用的路面同图4，车速对IRI值影响的模拟结果如图6。

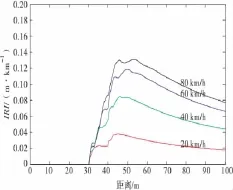
图6 检测车速对IRI测量的影响Fig.6 Influence of measure speed on IRI error

从图6中可以看出:车速越接近80 km/h，计算的IRI值与理论值偏差越小。

3 结语

1)实际检测过程中，IRI的测量精度主要受位移传感器精度、数据采样间隔、IRI评价距离、测量方向以及测量速度等多方面的影响。

2)对IRI影响最大的是位移传感器的精度，从分析结果中可知，要实现IRI一级精度检测，所采用的位移传感器精度至少达到0.1 mm。

3)采样间距对IRI的影响也较大，检测时采样间隔越小，IRI精度越高。

4)车速越接近80 km/h，IRI误差越小。检测时，只要让检测车速在高速范围内波动，就可以提高IRI测量精度。

5)检测方向对IRI测量结果影响较小。

［1］ Wei Hong.Development of Profiler Based Rideability Specifications for Flexible Pavement［D］.Columbia:University of South Carolina，2005.

［2］ 王建锋，马建，宋宏勋.路面三维检测技术研究［J］.武汉理工大学学报:通科学与工程版，2010，34(6):1202-1205.

Wang Jianfeng，Ma Jian，Song Hongxun.Road three-dimensional shape measurement method with multi-laser-sensors［J］.Journal of Wuhan University of Technology:Transportation Science＆Engineering，2010，34(6):1202-1205.

［3］ 张明，叶巧玲，冯晓.路面平整度检测技术现状与发展［J］.重庆交通大学学报:自然科学版，2007，26(4):122-126.

Zhang Ming，Ye Qiaoling，Feng Xiao.Actuality and development of the detection technology for road surface roughness［J］.Journal of Chongqing Jiaotong University:Natural Science，2007，26(4):122-126.

［4］ Sayers M W，Gillespie T D，Queiroz C A V.The International Road Roughness Experiment:Establishing Correlation and Calibration Standard for Measurements［R］.Washington，D.C.:World Bank，1986.

［5］ 宋一凡，陈榕峰.基于路面不平整度的车辆振动响应分析方法［J］.交通运输工程学报，2007，7(4):39-43.

Song Yifan，Chen Rongfeng.Analysis method of vehicle vibration response caused by pavement roughness［J］.Journal of Traffic and Transportation Engineering，2007，7(4):39-43.

［6］ 王建锋，马建，马荣贵.动位移的加速度精确测量技术研究［J］.计算机科学，2010，37(12):201-207.

Wang Jianfeng，Ma Jian，Ma Ronggui.Study on calculation of dynamic displacement from time-frequency integration of acceleration［J］.Computer Science，2010，37(12):201-207.

［7］ 王建锋.激光路面三维检测专用车技术与理论研究［D］.西安:长安大学，2010.

［8］ 马荣贵，宋宏勋，来旭光.激光路面平整度检测系统［J］.长安大学学报:自然科学版，2006，26(2):38-41.

Ma Ronggui，Song Hongxun，Lai Xuguang.Pavement roughness measurement system based on laser displacement sensors［J］.Journal of Chang’an University:Natural Science，2006，26(2):38-41.